数据结构与算法

常见数据结构总结

1.栈

基本理论

栈是一种后进先出（即 LIFO:Last in, First out）的数据结构，在JavaScript中没有栈的结构，但是可以用数组来实现栈的所有功能: push(入栈)和pop（出栈）

简易实现

function Stack() {
  this.stack = [];
  this.push = function (item) {
    this.stack.push(item);
  };
  this.pop = function () {
    this.stack.pop();
  };
}

应用

1）十进制转二进制

// 时间复杂度 O(n) n为二进制的长度
// 空间复杂度 O(n) n为二进制的长度
const dec2bin = (dec) => {
  // 创建一个字符串
  let res = "";

  // 创建一个栈
  let stack = [];

  // 遍历数字 如果大于0 就可以继续转换2进制
  while (dec > 0) {
    // 将数字的余数入栈
    stack.push(dec % 2);

    // 除以2
    dec = dec >> 1;
  }

  // 取出栈中的数字
  while (stack.length) {
    res += stack.pop();
  }

  // 返回这个字符串
  return res;
};
复制代码;

2）判断字符串的有效括号

// 时间复杂度O(n) n为s的length
// 空间复杂度O(n)
const isValid = (s) => {
  // 如果长度不等于2的倍数肯定不是一个有效的括号
  if (s.length % 2 === 1) return false;

  // 创建一个栈
  let stack = [];

  // 遍历字符串
  for (let i = 0; i < s.length; i++) {
    const c = s[i];

    // 如果是左括号就入栈
    if (c === "(" || c === "{" || c === "[") {
      stack.push(c);
    } else {
      // 如果不是左括号 且栈为空 肯定不是一个有效的括号 返回false
      if (!stack.length) return false;

      // 拿到最后一个左括号
      const top = stack[stack.length - 1];

      // 如果是右括号和左括号能匹配就出栈
      if (
        (top === "(" && c === ")") ||
        (top === "{" && c === "}") ||
        (top === "[" && c === "]")
      ) {
        stack.pop();
      } else {
        // 否则就不是一个有效的括号
        return false;
      }
    }
  }
  return stack.length === 0;
};

2.队列

队列是一种先进先出（即 FIFO:First in, First out）的数据结构，在JavaScript中没有队列的数据结构，不过我们依旧可以使用数组来实现队列的功能：enqueue（入队）和dequeue（出队）

简易实现

function Queue() {
  this.queue = [];
  this.enqueue = function (item) {
    this.queue.push(item);
  };
  this.dequeue = function () {
    return this.queue.shift();
  };
}

完全实现

function Queue() {
  //属性
  this.items = [];
  //方法
  // 1.将元素加入到队列中
  Queue.prototype.enqueue = function (element) {
    this.items.push(element);
  };
  // 2.从队列中删除前端元素
  Queue.prototype.dequeue = function () {
    return this.items.shift();
  };
  // 3.查看前端元素
  Queue.prototype.front = function () {
    return this.items[0];
  };
  // 4.查看队列是否为空
  Queue.prototype.isEmpty = function () {
    return this.items.length == 0;
  };
  // 5.查看队列元素的个数
  Queue.prototype.size = function () {
    return this.items.length;
  };
  // 6.toString
  Queue.prototype.toString = function () {
    var resultString = "";
    for (var i = 0; i < this.items.length; i++) {
      resultString += this.items[i] + " ";
    }
    return resultString;
  };
}
//使用
var queue = new Queue();

应用

1）最近的请求次数

var RecentCounter = function () {
  // 初始化队列
  this.q = [];
};

// 输入 inputs = [[],[1],[100],[3001],[3002]] 请求间隔为 3000ms
// 输出 outputs = [null,1,2,3,3]

// 时间复杂度 O(n) n为剔出老请求的长度
// 空间复杂度 O(n) n为最近请求的次数
RecentCounter.prototype.ping = function (t) {
  // 如果传入的时间小于等于最近请求的时间，则直接返回0
  if (!t) return null;

  // 将传入的时间放入队列
  this.q.push(t);

  // 如果队头小于 t - 3000 则剔除队头
  while (this.q[0] < t - 3000) {
    this.q.shift();
  }

  // 返回最近请求的次数
  return this.q.length;
};

3.链表

链接也是由多个元素组成的列表，但是与队列和栈不同的是，链表的存储是不连续的，而是使用 next 指向下一个元素。在链表中，我们需要添加删除元素，只需要修改 next 指针即可。在js中我们可以用object来模拟链表。

简单实现

function ListNode(val, next) {
  this.val = val === undefined ? 0 : val;
  this.next = next === undefined ? null : next;
}

完全实现

//封装链表的类
function LinkedList() {
  //内部的类:节点类
  function Node(data) {
    this.data = data;
    this.next = null;
  }
  //属性
  this.head = null;
  //用于记录链表的长度
  this.length = 0;

  //1.追加方法
  LinkedList.prototype.append = function (data) {
    //1.创建新节点
    var newNode = new Node(data);
    //2.判断是否添加的是第一个节点
    if (this.length === 0) {
      //2.1是第一个节点
      this.head = newNode;
    } else {
      //2.2不是第一个节点
      //找到最后一个节点
      var current = this.head;
      while (current.next) {
        current = current.next;
      }
      //最后节点的next指向新的节点
      current.next = newNode;
    }

    //3.length+1
    this.length += 1;
  };
  //2.toString方法
  LinkedList.prototype.toString = function () {
    //1.定义变量
    var current = this.head;
    var listString = "";
    //2.循环获取一个个的节点
    while (current) {
      listString += current.data + " ";
      current = current.next;
    }
    return listString;
  };
  //3.insert方法
  LinkedList.prototype.insert = function (position, data) {
    //1.对position进行越界判断
    //负数判断，长度判断
    if (position < 0 || position > this.length) return false;

    //2.根据data创建newNode
    var newNode = new Node(data);

    //3.判断插入的位置是否是第一个
    if (position == 0) {
      //让新节点的next指向head的指针,而head的指针真好指向原先的第一个
      newNode.next = this.head;
      //再让head指向新的节点
      this.head = newNode;
      this.length += 1;
    } else {
      var index = 0;
      var current = this.head;
      var previous = null;
      while (index++ < position) {
        previous = current;
        current = current.next;
      }
      newNode.next = current;
      previous.next = newNode;
      this.length += 1;
    }
  };
  //4.get方法
  LinkedList.prototype.get = function (position) {
    //1.对position进行越界判断
    //负数判断，长度判断
    if (position < 0 || position >= this.length) return null;
    //2.获取对应的data
    var current = this.head;
    var index = 0;
    while (index++ < position) {
      current = current.next;
    }
    return current.data;
  };
  //5.indexOf方法
  LinkedList.prototype.indexOf = function (data) {
    //1.定义变量
    var current = this.head;
    var index = 0;
    //2.开始查找
    while (current) {
      if (current.data === data) {
        return index;
      } else {
        current = current.next;
        index += 1;
      }
    }
    //找到最后没有找到，返回-1
    return -1;
  };
  //6.update方法
  LinkedList.prototype.update = function (position, newData) {
    //1.对position进行越界判断
    //负数判断，长度判断
    if (position < 0 || position >= this.length) return false;
    //2.获取对应的data
    var current = this.head;
    var index = 0;
    while (index++ < position) {
      current = current.next;
    }
    //将position位置的data替换成新data
    current.data = newData;
  };
  //7.removeAt方法
  LinkedList.prototype.removeAt = function (position, newData) {
    //1.对position进行越界判断
    //负数判断，长度判断
    if (position < 0 || position >= this.length) return null;
    //2.判断是否删除的是第一个节点
    var current = this.head;
    if (position === 0) {
      this.head = this.head.next;
    } else {
      var index = 0;
      var previous = null;
      while (index++ < position) {
        previous = current;
        current = current.next;
      }
      //让前一个节点的next指向current的next
      previous.next = current.next;
    }

    //3.length-1
    this.length -= 1;
    return current.data;
  };
  //8.remove方法
  LinkedList.prototype.remove = function (data) {
    //1.获取data在列表中的位置
    var position = this.indexOf(data);
    //2.根据位置信息删除节点
    return this.removeAt(position);
  };
  //9.isEmpty方法
  LinkedList.prototype.isEmpty = function () {
    return this.length === 0;
  };
  //10.size方法
  LinkedList.prototype.size = function () {
    return this.length;
  };
}

var list = new LinkedList();

应用

1）手写 instanceOf

const myInstanceOf = (A, B) => {
  // 声明一个指针
  let p = A;

  // 遍历这个链表
  while (p) {
    if (p === B.prototype) return true;
    p = p.__proto__;
  }

  return false;
};

myInstanceOf([], Object);

2）删除链表中的节点

// 时间复杂和空间复杂度都是 O(1)
const deleteNode = (node) => {
  // 把当前链表的指针指向下下个链表的值就可以了
  node.val = node.next.val;
  node.next = node.next.next;
};

3）删除排序链表中的重复元素

// 1 -> 1 -> 2 -> 3 -> 3
// 1 -> 2 -> 3 -> null

// 时间复杂度 O(n) n为链表的长度
// 空间复杂度 O(1)
const deleteDuplicates = (head) => {
  // 创建一个指针
  let p = head;

  // 遍历链表
  while (p && p.next) {
    // 如果当前节点的值等于下一个节点的值
    if (p.val === p.next.val) {
      // 删除下一个节点
      p.next = p.next.next;
    } else {
      // 否则继续遍历
      p = p.next;
    }
  }

  //  最后返回原来链表
  return head;
};

4）反转链表

// 1 -> 2 -> 3 -> 4 -> 5 -> null
// 5 -> 4 -> 3 -> 2 -> 1 -> null

// 时间复杂度 O(n) n为链表的长度
// 空间复杂度 O(1)
var reverseList = function (head) {
  // 创建一个指针
  let p1 = head;

  // 创建一个新指针
  let p2 = null;

  // 遍历链表
  while (p1) {
    // 创建一个临时变量
    const tmp = p1.next;

    // 将当前节点的下一个节点指向新链表
    p1.next = p2;

    // 将新链表指向当前节点
    p2 = p1;

    // 将当前节点指向临时变量
    p1 = tmp;
  }

  // 最后返回新的这个链表
  return p2;
};

reverseList(list);

4.集合和字典

集合

一种无序且唯一的数据结构

ES6 中有集合 Set 类型

const arr = [1, 1, 1, 2, 2, 3];

// 去重
const arr2 = [...new Set(arr)];

// 判断元素是否在集合中
const set = new Set(arr);
set.has(2); // true

//  交集
const set2 = new Set([1, 2]);
const set3 = new Set([...set].filter((item) => set.has(item)));

两个数组的交集

// 时间复杂度 O(n^2) n为数组长度
// 空间复杂度 O(n)  n为去重后的数组长度
const intersection = (nums1, nums2) => {
  // 通过数组的filter选出交集
  // 然后通过 Set集合 去重 并生成数组
  return [...new Set(nums1.filter((item) => nums2.includes(item)))];
};

字典

与集合类似，一个存储唯一值的结构,以键值对的形式存储

js 中有字典数据结构 就是 Map 类型

哈希函数

哈希函数，把学生的姓名直接映射为哈希表上的索引，然后就可以通过查询索引下标快速知道这位同学是否在这所学校里了。

哈希函数如下图所示，通过 hashCode 把名字转化为数值，一般 hashcode 是通过特定编码方式，可以将其他数据格式转化为不同的数值，这样就把学生名字映射为哈希表上的索引数字了。

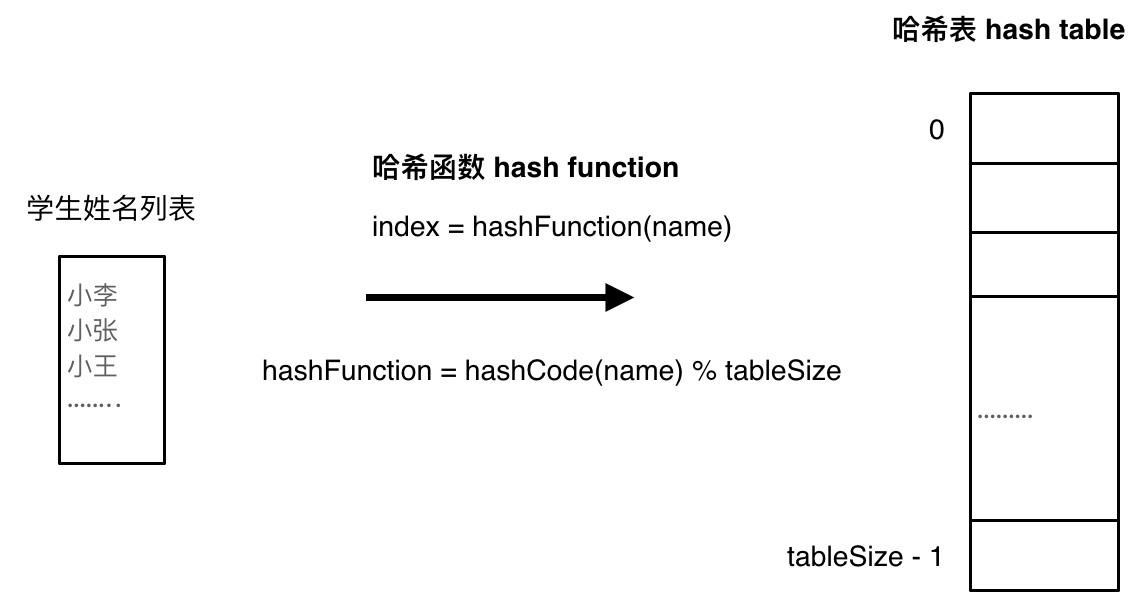
如果 hashCode 得到的数值大于 哈希表的大小了，也就是大于 tableSize 了，怎么办呢？

此时为了保证映射出来的索引数值都落在哈希表上，我们会在再次对数值做一个取模的操作，就要我们就保证了学生姓名一定可以映射到哈希表上了。

此时问题又来了，哈希表我们刚刚说过，就是一个数组。

如果学生的数量大于哈希表的大小怎么办，此时就算哈希函数计算的再均匀，也避免不了会有几位学生的名字同时映射到哈希表 同一个索引下标的位置。

接下来哈希碰撞登场

哈希碰撞

如图所示，小李和小王都映射到了索引下标 1 的位置，这一现象叫做哈希碰撞。

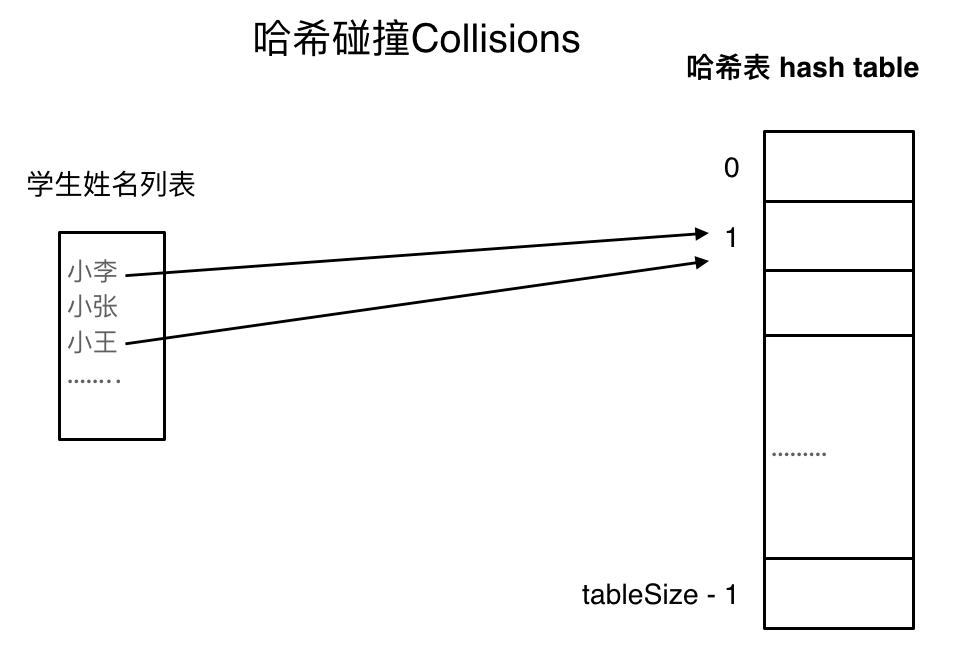
一般哈希碰撞有两种解决方法， 拉链法和线性探测法。

拉链法

刚刚小李和小王在索引 1 的位置发生了冲突，发生冲突的元素都被存储在链表中。 这样我们就可以通过索引找到小李和小王了

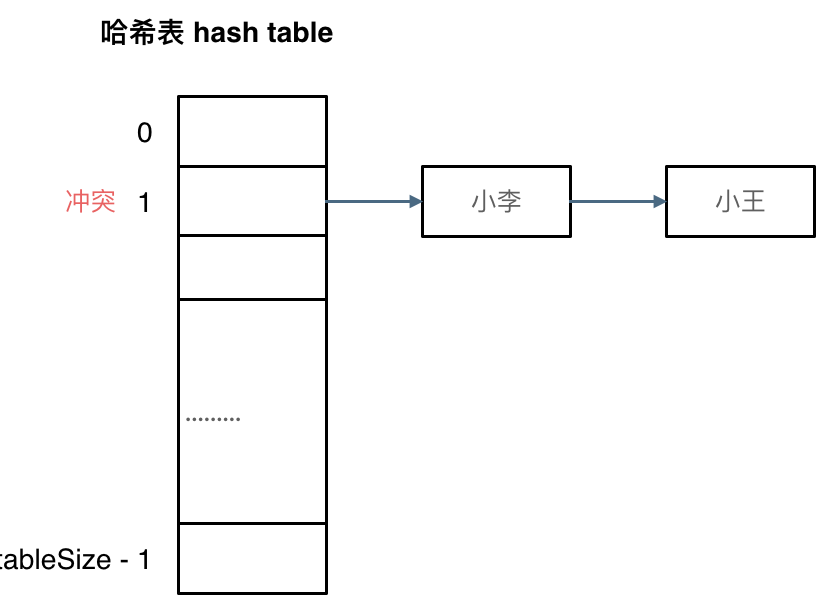
（数据规模是 dataSize， 哈希表的大小为 tableSize）

其实拉链法就是要选择适当的哈希表的大小，这样既不会因为数组空值而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间。

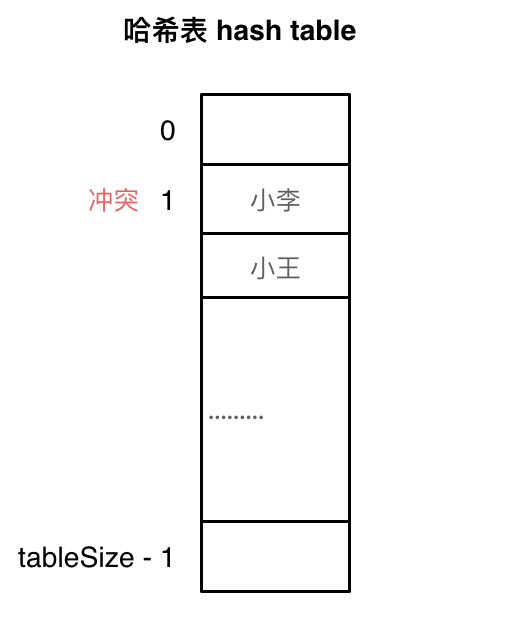
线性探测法

使用线性探测法，一定要保证 tableSize 大于 dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。

例如冲突的位置，放了小李，那么就向下找一个空位放置小王的信息。所以要求 tableSize 一定要大于 dataSize ，要不然哈希表上就没有空置的位置来存放 冲突的数据了。如图所示：

1）两数之和

// nums = [2, 7, 11, 15] target = 9

// 时间复杂度O(n) n为nums的length
// 空间复杂度O(n)
var twoSum = function (nums, target) {
  // 建立一个字典数据结构来保存需要的值
  const map = new Map();
  for (let i = 0; i < nums.length; i++) {
    // 获取当前的值，和需要的值
    const n = nums[i];
    const n2 = target - n;

    // 如字典中有需要的值，就匹配成功
    if (map.has(n2)) {
      return [map.get(n2), i];
    } else {
      // 如没有，则把需要的值添加到字典中
      map.set(n, i);
    }
  }
};

2）两个数组的交集

// nums1 = [1,2,2,1], nums2 = [2,2]
// 输出：[2]

// 时间复杂度 O(m + n) m为nums1长度 n为nums2长度
// 空间复杂度 O(m) m为交集的数组长度
const intersection = (nums1, nums2) => {
  // 创建一个字典
  const map = new Map();

  // 将数组1中的数字放入字典
  nums1.forEach((n) => map.set(n, true));

  // 创建一个新数组
  const res = [];

  // 将数组2遍历 并判断是否在字典中
  nums2.forEach((n) => {
    if (map.has(n)) {
      res.push(n);

      // 如果在字典中，则删除该数字
      map.delete(n);
    }
  });

  return res;
};

3）字符的有效的括号

// 用字典优化

// 时间复杂度 O(n) n为s的字符长度
// 空间复杂度 O(n)
const isValid = (s) => {
  // 如果长度不等于2的倍数肯定不是一个有效的括号
  if (s.length % 2 !== 0) return false;

  // 创建一个字典
  const map = new Map();
  map.set("(", ")");
  map.set("{", "}");
  map.set("[", "]");

  // 创建一个栈
  const stack = [];

  // 遍历字符串
  for (let i = 0; i < s.length; i++) {
    // 取出字符
    const c = s[i];

    // 如果是左括号就入栈
    if (map.has(c)) {
      stack.push(c);
    } else {
      // 取出栈顶
      const t = stack[stack.length - 1];

      // 如果字典中有这个值 就出栈
      if (map.get(t) === c) {
        stack.pop();
      } else {
        // 否则就不是一个有效的括号
        return false;
      }
    }
  }

  return stack.length === 0;
};

4）最小覆盖字串

// 输入：s = "ADOBECODEBANC", t = "ABC"
// 输出："BANC"

// 时间复杂度 O(m + n) m是t的长度 n是s的长度
// 空间复杂度 O(k) k是字符串中不重复字符的个数
var minWindow = function (s, t) {
  // 定义双指针维护一个滑动窗口
  let l = 0;
  let r = 0;

  // 建立一个字典
  const need = new Map();

  //  遍历t
  for (const c of t) {
    need.set(c, need.has(c) ? need.get(c) + 1 : 1);
  }

  let needType = need.size;

  // 记录最小子串
  let res = "";

  // 移动右指针
  while (r < s.length) {
    // 获取当前字符
    const c = s[r];

    // 如果字典里有这个字符
    if (need.has(c)) {
      // 减少字典里面的次数
      need.set(c, need.get(c) - 1);

      // 减少需要的值
      if (need.get(c) === 0) needType -= 1;
    }

    // 如果字典中所有的值都为0了 就说明找到了一个最小子串
    while (needType === 0) {
      // 取出当前符合要求的子串
      const newRes = s.substring(l, r + 1);

      // 如果当前子串是小于上次的子串就进行覆盖
      if (!res || newRes.length < res.length) res = newRes;

      // 获取左指针的字符
      const c2 = s[l];

      // 如果字典里有这个字符
      if (need.has(c2)) {
        // 增加字典里面的次数
        need.set(c2, need.get(c2) + 1);

        // 增加需要的值
        if (need.get(c2) === 1) needType += 1;
      }
      l += 1;
    }
    r += 1;
  }
  return res;
};

5.二叉树

基础

树是一种分层数据的抽象模型，在JavaScript中没有树这个数据结构，所以通常我们使用Object来模拟一个树的结构

• 节点的高度：节点到叶子节点的最长路径（边数）
• 节点的深度：根节点到这个节点所经历的边的个数
• 节点的层数：节点的深度 +1
• 树的高度：根节点的高度

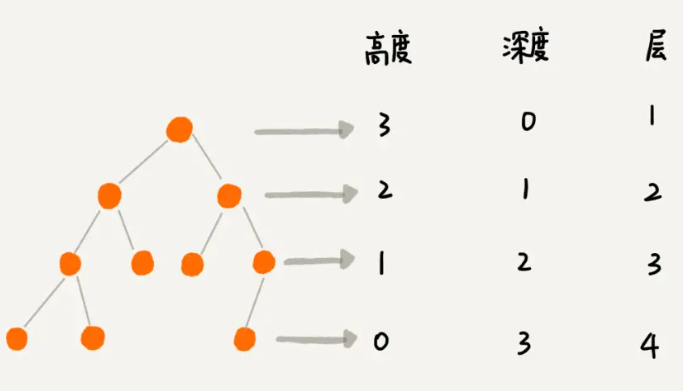
二叉树的度是指树中所以结点的度数的最大值。二叉树的度小于等于 2，因为二叉树的定义要求二叉树中任意结点的度数（结点的分支数）小于等于 2

二叉树叶子结点总数为 n0，度为 2 的结点个数为 n2，则 n0=n2+1

假设该二叉树总共有 n 个结点(n=n0+n1+n2)，则该二叉树总共会有 n-1 条边，度为 2 的结点会延伸出两条边，

同理，度为 1 的结点会延伸出一条边，则可列公式：n-1 = 2n2 + 1n1 ，

合并两个式子可得：2n2 + 1n1 +1 =n0 + n1 + n2 ，则计算可知 n0=n2+1

如果完全二叉树有 n 个结点，那么树最高为 log2(n)+1

存储方法

存储二叉树有两种方法，

• 基于指针或者引用的二叉链式存储法，
• 基于数组的顺序存储法。

1）链式存储法。 从下图可以看到，每个节点有三个字段，其中一个存储数据，另外两个是指向左右子节点的指针。我们只要拎住根节点，就可以通过左右子节点的指针，把整棵树都串起来。这种存储方式比较常用。大部分二叉树代码都是通过这种结构来实现的。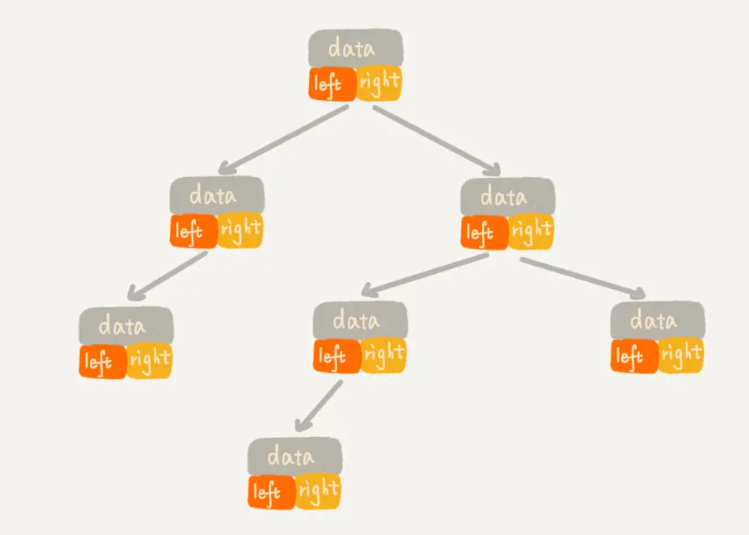

2）顺序存储法。 把根节点存储在下标 i = 1 的位置，那左子节点存储在下标 2 i = 2 的位置，右子节点存储在 2 i + 1 = 3 的位置。以此类推，B 节点的左子节点存储在 2 i = 2 2 = 4 的位置，右子节点存储在 2 i + 1 = 2 2 + 1 = 5 的位置。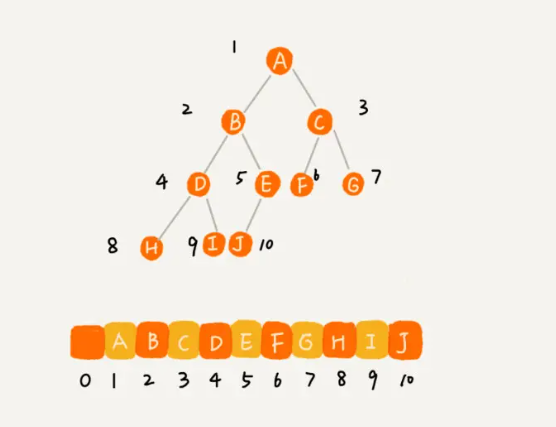

如果节点 X 存储在数组中下标为 i 的位置，下标为 2 i 的位置存储的就是左子节点，下标为 2 i + 1 的位置存储的就是右子节点。反过来，下标为 i/2 的位置存储就是它的父节点。通过这种方式，只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为 1 的位置），这样就可以通过下标计算，把整棵树都串起来。

不过，上面是一棵完全二叉树，所以仅仅“浪费”了一个下标为 0 的存储位置。如果是非完全二叉树，其实会浪费比较多的数组存储空间。看下面这个例子：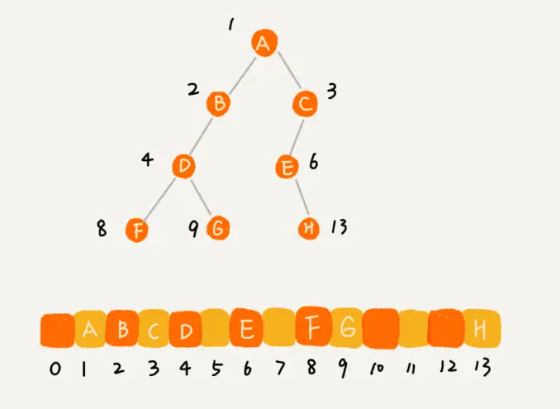

所以，如果某棵二叉树是一棵完全二叉树，那用数组存储无疑是最节省内存的一种方式。因为数组的存储方式并不需要像链式存储法那样，要存储额外的左右子节点的指针。这也是为什么完全二叉树会单独拎出来的原因，也是为什么完全二叉树要求最后一层的子节点都靠左的原因

二叉树分类

满二叉树

除了最后一层的节点没有任何子节点外，每层上的所有节点都有两个节点的二叉树

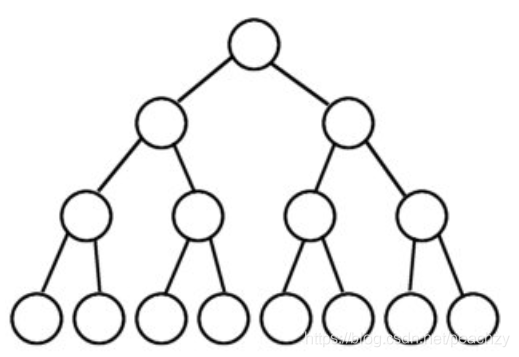
根据满二叉树的定义，得到其特点为：

1. 叶子只能出现在最下一层。
2. 非叶子结点度一定是 2。
3. 在同样深度的二叉树中，满二叉树的结点个数最多，叶子树最多。

完全二叉树

一颗二叉树的深度为 h，除了第 h 层外，其他各层的节点都有两个子节点，且第 h 层的所有节点都集中在最左边 （满二叉树一定是完全二叉树，但是完全二叉树不一定是满二叉树）

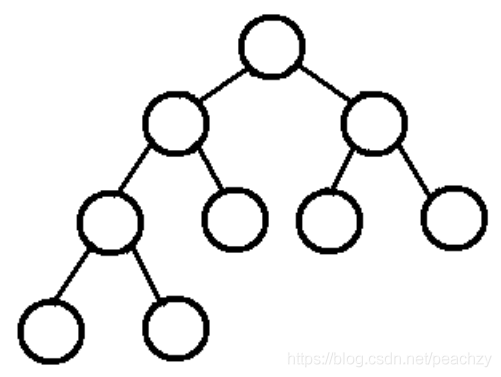
二叉搜索树

左子树的所有节点的值均小于它的根节点的值 右子树的所有节点的值均大于它的根节点的值 它的左右子树也分别为二叉搜索树

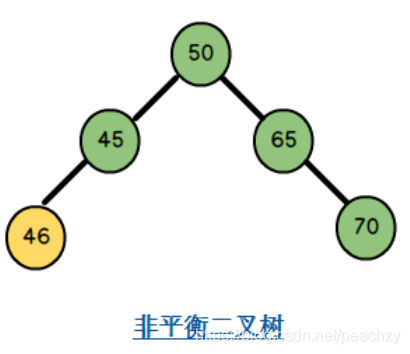
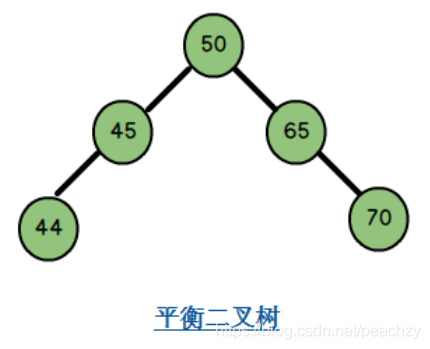
平衡二叉树

平衡二叉树是一颗高度平衡的二叉搜索树；左右两个子树的高度差绝对值不超过 1，且左右两个子树都是平衡二叉树； 通过左旋右旋来实现平衡；

红黑树

一种弱平衡的二叉搜索树 1、每个结点要么是红的，要么是黑的 2、根节点是黑的 3、如果一个结点是红色的，那么它的两个子节点都是黑的 4、每个叶节点都是黑的 （由于是弱平衡，可以看到，在相同的节点的情况下，AVL 树的高度低于红黑树），相对于严格要求的 AVL 树来说，它的旋转次数少，所哟对于搜索，插入和删除操作较多的情况下，我们就用红黑树。

堆

堆是完全二叉树，所以一定是平衡二叉树。 分为大顶堆和小顶堆 在大顶堆中：父节点的值比每一个子节点的值都要大 在小顶堆中：父节点的值比每一个子节点的值都要小

注意：堆的根节点中存放的是最大或者最小的元素，但是其他节点的排序是未知 例如：在一个大顶堆中，最大的那一个元素总是位于 index 0 的位置，但是最小的元素则未必是最后一个元素。唯一能保证的是最小的元素是一个叶节点，但是不确定是哪一个。

插入、删除、查找的时间复杂度 二叉搜索树：最好 logn 最坏 n 参考 平衡二叉搜索树：logn 红黑树：logn

简单实现

function TreeNode(val, left, right) {
  this.val = val === undefined ? 0 : val;
  this.left = left === undefined ? null : left;
  this.right = right === undefined ? null : right;
}

由数组构建二叉树

// 新建树节点类
class TreeNode {
  constructor(val, left, right) {
    this.val = val === undefined ? 0 : val;
    this.left = left === undefined ? null : left;
    this.right = right === undefined ? null : right;
  }
}
// 入参一个数组，生成二叉树
function buildTree(arr) {
  // 若没有参数或数组长度为0，则视为空树
  if (!arr || arr.length === 0) {
    return null;
  }

  // 先将数组第一个元素 设置为根结点
  let root = new TreeNode(arr.shift());

  // 节点队列 陆续从数组中为节点添加左右叶子
  let nodeQueue = [root];

  // 当数组剩余仍有元素，则持续为最近的节点添加叶子
  while (arr.length > 0) {
    // 从节点数组头部取出节点 为了添加叶子备用
    let node = nodeQueue.shift();

    // 若数组中无元素，则视为无叶子可添加,返回即可
    if (!arr.length) {
      break;
    }

    // 先从节点数组中取一个元素 转化为节点 拼接为左叶子
    let left = new TreeNode(arr.shift());
    node.left = left;
    nodeQueue.push(left);

    // 每拼接一片叶子节点 重新判断剩余叶子数量 若无剩余视为拼接完毕
    if (!arr.length) {
      break;
    }

    // 左侧叶子拼完，右边一样的操作
    let right = new TreeNode(arr.shift());
    node.right = right;
    nodeQueue.push(right);
  }

  // 最后返回根结点，通过根结点就能得到整个二叉树的结构
  return root;
}
// 测试
let arr = [1, 2, 3, 4, 5, 6, 7, 8, 9];
console.log(buildTree(arr));

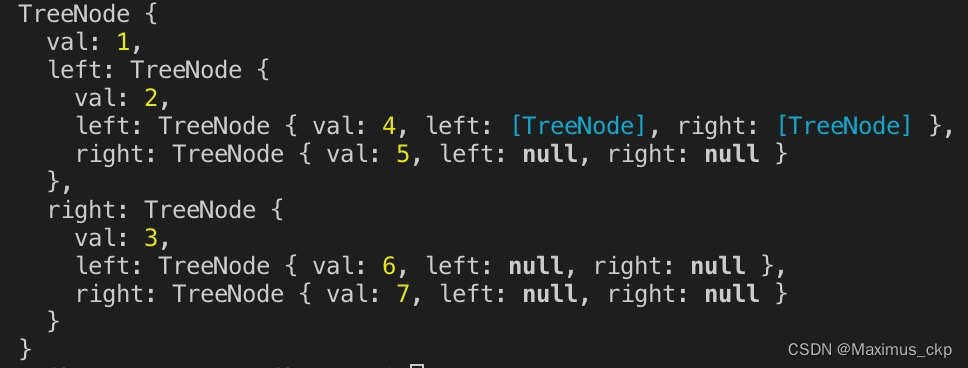
//封装二叉搜索树
function BinarySearchTree() {
  //节点
  function Node(key) {
    this.key = key;
    this.left = null;
    this.right = null;
  }
  //属性
  this.root = null;
  //方法
  //1.1插入数据
  BinarySearchTree.prototype.insert = function (key) {
    //1.根据key创建节点
    var newNode = new Node(key);

    //2.判断根节点是否有值
    if (this.root == null) {
      this.root = newNode;
    } else {
      this.insertNode(this.root, newNode);
    }
  };
}

深度优先搜索

• 尽可能深的搜索树的分支,就比如遇到一个节点就会直接去遍历他的子节点，不会立刻去遍历他的兄弟节点

树的深度优先遍历即有 children 就继续遍历 children，直到没有 children 后再遍历下一个结点: 深度优先遍历流程：

1. 访问根结点
2. 对根结点的 children 继续深度优先遍历

function des(root) {
  console.log("value", root.value);
  root.children.forEach((item) => {
    des(item);
  });
}

des(treeData);

广度优先搜索

• 先访问离根节点最近的节点, 如果有兄弟节点就会先遍历兄弟节点，再去遍历自己的子节点

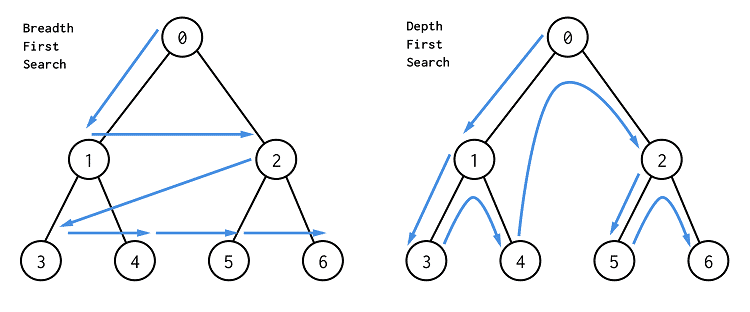
广度优先遍历即优先遍历子结点，如果子结点遍历完成，则遍历各子结点的 children： 广度优先遍历流程：

创建一个数组，将根结点作为第一项 将数组中第一项弹出并访问 将弹出项中的 children 遍历并依次添加至数组中 重复 2、3 步骤直到队列为空

function bfs(root) {
  let arr = [root];

  while ((tree = arr.shift())) {
    console.log("value", tree.value);
    tree.children.forEach((item) => {
      arr.push(item);
    });
  }
}

bfs(treeData);

递归（前中后序遍历）

//时间复杂度O(n),n为节点个树，空间复杂度O(n)，即递归的空间开销(树的高度)，最坏的情况下树是链表，所以是O(n)，平均空间复杂度O(logn)
//前序遍历:
var preorderTraversal = function (root, res = []) {
  if (!root) return res;
  res.push(root.val);
  preorderTraversal(root.left, res);
  preorderTraversal(root.right, res);
  return res;
};

//中序遍历:
var inorderTraversal = function (root, res = []) {
  if (!root) return res;
  inorderTraversal(root.left, res);
  res.push(root.val);
  inorderTraversal(root.right, res);
  return res;
};

//后序遍历:
var postorderTraversal = function (root, res = []) {
  if (!root) return res;
  postorderTraversal(root.left, res);
  postorderTraversal(root.right, res);
  res.push(root.val);
  return res;
};

非递归（前中后序遍历）

前序遍历

var preorderTraversal = function (root) {
  const res = [];
  const stack = [];
  while (root || stack.length) {
    while (root) {
      res.push(root.val);
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    root = root.right;
  }
  return res;
};

中序遍历

const inorderTraversal = (root) => {
  if (!root) return [];
  const res = [];
  const stack = [];
  while (root || stack.length) {
    while (root) {
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    res.push(root.val);
    root = root.right;
  }
  return res;
};

后序遍历

var postorderTraversal = function (root) {
  const res = [];
  const stack = [];
  while (root || stack.length) {
    while (root) {
      stack.push(root);
      res.unshift(root.val);
      root = root.right;
    }
    root = stack.pop();
    root = root.left;
  }
  return res;
};

层序遍历

递归

var levelOrder = function (root) {
  if (!root) return [];
  var res = [];
  helper(root, 0);
  function helper(node, level) {
    if (!node) return;
    if (!res[level]) {
      res[level] = [node.val];
    } else {
      res[level].push(node.val);
    }
    var left = node.left;
    var right = node.right;
    helper(left, level + 1);
    helper(right, level + 1);
  }
  return res;
};

非递归（队列实现）

var levelOrder = function (root) {
  let res = [],
    queue = [];
  queue.push(root);
  if (root === null) {
    return res;
  }
  while (queue.length !== 0) {
    let length = queue.length;
    let curLevel = [];
    for (let i = 0; i < length; i++) {
      let node = queue.shift();
      curLevel.push(node.val);
      node.left && queue.push(node.left);
      node.right && queue.push(node.right);
    }
    res.push(curLevel);
  }
  return res;
};

6.堆

基本理论

堆是一种特殊的完全二叉树，堆中的所有所有结点都大于等于或小于等于他的子结点，若大于等于子结点则为最大堆，否则为最小堆。在javaScript中通常使用数组来表示堆 对于第i个结点: 其父结点的索引为：Math.floor((i - 1) / 2) 其左子结点的索引为：(2 * i) + 1 其右子结点的索引为：(2 * i) + 2

如果是排序，求升序用大顶堆，求降序用小顶堆。 一般我们说 topK 问题，就可以用大顶堆或小顶堆来实现， 最大的 K 个：小顶堆 最小的 K 个：大顶堆这里是引用

为什么升序要用大顶堆呢？

上面提到过大顶堆的特点：每个结点的值都大于或等于其左右孩子结点的值，我们把大顶堆构建完毕后根节点的值一定是最大的，然后把根节点的和最后一个元素（也可以说最后一个节点）交换位置，那么末尾元素此时就是最大元素了（理解这点很重要）

知道了堆排序的原理下面就可以来操作了，在进行操作前先理清一下步骤（假设我们想要升序的排列）

1. 先 n 个元素的无序序列，构建成大顶堆
2. 将根节点与最后一个元素交换位置（将最大元素"沉"到数组末端）
3. 交换过后可能不再满足大顶堆的条件，所以需要将剩下的 n-1 个元素重新构建成大顶堆
4. 重复第二步、第三步直到整个数组排序完成

上面我们实现了一个简单构建最小堆的方法，那么实现堆排序的原理其实就是先构建一个最小堆然后将堆顶（最小值弹出），再将其他元素构建堆，每次都弹出堆顶元素直到剩余元素为 1 时结束，这样就是实现了一个堆排序

function MinHeap() {
  this.heap = [];

  this.getParentIndex = function (childIndex) {
    return Math.floor((childIndex - 1) / 2);
  };
  /**
   * 交换位置
   * @param {number} index1
   * @param {number} index2
   */
  this.swap = function (index1, index2) {
    const temp = this.heap[index1];
    this.heap[index1] = this.heap[index2];
    this.heap[index2] = temp;
  };

  /**
   * 上移到合适位置,和父结点比较，如果比父结点小则交换
   * @param {number} index 索引
   */
  this.moveUp = function (index) {
    if (index === 0) return;
    const parentIndex = this.getParentIndex(index);
    if (this.heap[index] < this.heap[parentIndex]) {
      this.swap(index, parentIndex);
      this.moveUp(parentIndex);
    }
  };
  /**
   * 添加元素
   * @param {number} value
   */
  this.append = function (value) {
    this.heap.push(value);
    this.moveUp(this.heap.length - 1);
  };
}

const minHeap = new MinHeap();
minHeap.append(3);
minHeap.append(4);
minHeap.append(1);
minHeap.append(0);
minHeap.append(2);
minHeap.append(7);
minHeap.append(9);
// [0, 1, 3, 4, 2, 7, 9]

应用

1）JS 实现一个最小堆

// js实现最小堆类
class MinHeap {
  constructor() {
    // 元素容器
    this.heap = [];
  }

  // 交换节点的值
  swap(i1, i2) {
    [this.heap[i1], this.heap[i2]] = [this.heap[i2], this.heap[i1]];
  }

  //  获取父节点
  getParentIndex(index) {
    // 除以二， 取余数
    return (index - 1) >> 1;
  }

  // 获取左侧节点索引
  getLeftIndex(i) {
    return (i << 1) + 1;
  }

  // 获取右侧节点索引
  getRightIndex(i) {
    return (i << 1) + 2;
  }

  // 上移
  shiftUp(index) {
    if (index == 0) return;

    // 获取父节点
    const parentIndex = this.getParentIndex(index);

    // 如果父节点的值大于当前节点的值 就需要进行交换
    if (this.heap[parentIndex] > this.heap[index]) {
      this.swap(parentIndex, index);

      // 然后继续上移
      this.shiftUp(parentIndex);
    }
  }

  // 下移
  shiftDown(index) {
    // 获取左右节点索引
    const leftIndex = this.getLeftIndex(index);
    const rightIndex = this.getRightIndex(index);

    // 如果左子节点小于当前的值
    if (this.heap[leftIndex] < this.heap[index]) {
      // 进行节点交换
      this.swap(leftIndex, index);

      // 继续进行下移
      this.shiftDown(leftIndex);
    }

    // 如果右侧节点小于当前的值
    if (this.heap[rightIndex] < this.heap[index]) {
      this.swap(rightIndex, index);
      this.shiftDown(rightIndex);
    }
  }

  // 插入元素
  insert(value) {
    // 插入到堆的底部
    this.heap.push(value);

    // 然后上移： 将这个值和它的父节点进行交换，知道父节点小于等于这个插入的值
    this.shiftUp(this.heap.length - 1);
  }

  // 删除堆项
  pop() {
    // 把数组最后一位 转移到数组头部
    this.heap[0] = this.heap.pop();

    // 进行下移操作
    this.shiftDown(0);
  }

  // 获取堆顶元素
  peek() {
    return this.heap[0];
  }

  // 获取堆大小
  size() {
    return this.heap.length;
  }
}

2）数组中的第 k 个最大元素

// 输入 [3,2,1,5,6,4] 和 k = 2
// 输出 5

// 时间复杂度 O(n * logK) K就是堆的大小
// 空间复杂度 O(K) K是参数k
var findKthLargest = function (nums, k) {
  // 使用上面js实现的最小堆类，来构建一个最小堆
  const h = new MinHeap();

  // 遍历数组
  nums.forEach((n) => {
    // 把数组中的值依次插入到堆里
    h.insert(n);

    if (h.size() > k) {
      // 进行优胜劣汰
      h.pop();
    }
  });

  return h.peek();
};

3）前 K 个高频元素

// nums = [1,1,1,2,2,3], k = 2
// 输出: [1,2]

// 时间复杂度 O(n * logK)
// 空间复杂度 O(k)
var topKFrequent = function (nums, k) {
  // 统计每个元素出现的频率
  const map = new Map();

  // 遍历数组 建立映射关系
  nums.forEach((n) => {
    map.set(n, map.has(n) ? map.get(n) + 1 : 1);
  });

  // 建立最小堆
  const h = new MinHeap();

  // 遍历映射关系
  map.forEach((value, key) => {
    // 由于插入的元素结构发生了变化，所以需要对 最小堆的类 进行改造一下,改造的方法我会写到最后
    h.insert({ value, key });
    if (h.size() > k) {
      h.pop();
    }
  });
  return h.heap.map((item) => item.key);
};

// 改造上移和下移操作即可
// shiftUp(index) {
//   if (index == 0) return;
//   const parentIndex = this.getParentIndex(index);
//   if (this.heap[parentIndex] && this.heap[parentIndex].value > this.heap[index].value) {
//     this.swap(parentIndex, index);
//     this.shiftUp(parentIndex);
//   }
// }
// shiftDown(index) {
//   const leftIndex = this.getLeftIndex(index);
//   const rightIndex = this.getRightIndex(index);

//   if (this.heap[leftIndex] && this.heap[leftIndex].value < this.heap[index].value) {
//     this.swap(leftIndex, index);
//     this.shiftDown(leftIndex)
//   }

//   if (this.heap[rightIndex] && this.heap[rightIndex].value < this.heap[index].value) {
//     this.swap(rightIndex, index);
//     this.shiftDown(rightIndex)
//   }
// }

7.图

「数据结构」在 JavaScript 中实现图

图结构是一种常见的数据结构。数学上有一个重要的分支叫做图论，其起源与“欧拉七桥”问题有关。图论主要用于研究顶点和边组成的图形的数学理论和方法，应用于生活之中，就是研究事物（顶点）与事物之间的关系（边），比如地铁线路图。

基本理论

什么是图

• 图是网络结构的抽象模型。
• 图是一组由边连接的节点（或顶点）。 因为任何二元关系都可以用图来表示，所以图的学习就显得尤为重要。

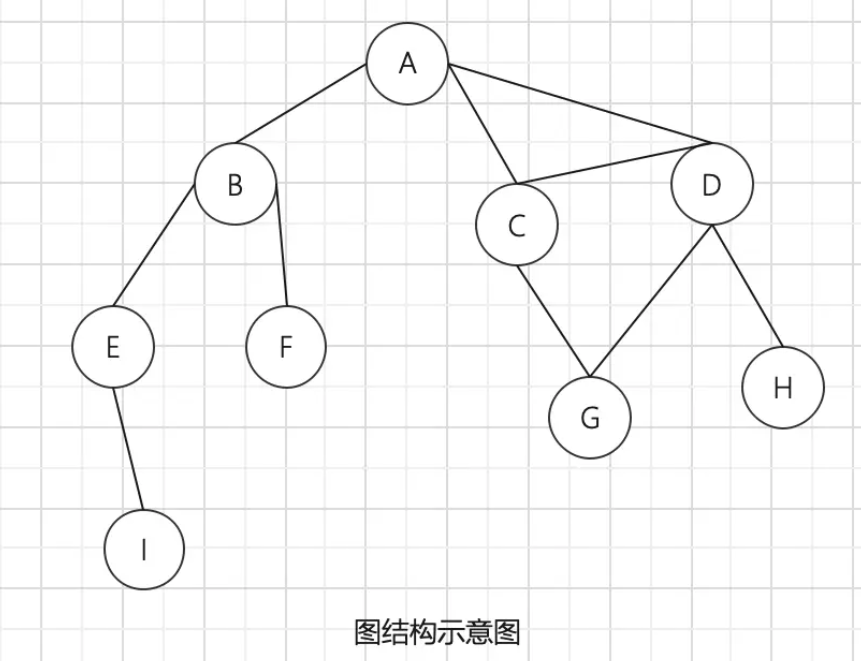
图在数学和技术上的概念

一个图 G = (V, E)由以下元素组成。

• V：一组顶点。
• E：一组边，连接 V 中的顶点。

图的相关术语

• 相邻顶点：由一条边连接在一起的顶点。上图中，A 和 B 是相邻的，A 和 D 是相邻的，A 和 C 是相邻的，A 和 E 不是相邻的。
• 度：一个顶点的度是其相邻顶点的数量。上图中，A 和其他三个顶点相连接，因此 A 的度为 3；E 和其他两个顶点相连，因此 E 的度为 2。
• 路径：是顶点 v1, v2, …, vk 的一个连续序列，其中 vi 和 vi+1 是相邻的。在上图中，其中包含路径 A B E I 和 A C D G。
• 简单路径要求不包含重复的顶点 比如，上图中的 A D G 就是一条简单路径。
• 环也是一个简单路径，因为环的最后一个顶点和第一个顶点是同一个顶点。比如说上图中的 A D C A 环。
• 如果图中不存在环，则称该图是无环的。
• 如果图中每两个顶点间都存在路径，则该图是连通的。

图的种类

• 有向图：是指图的边有方向。

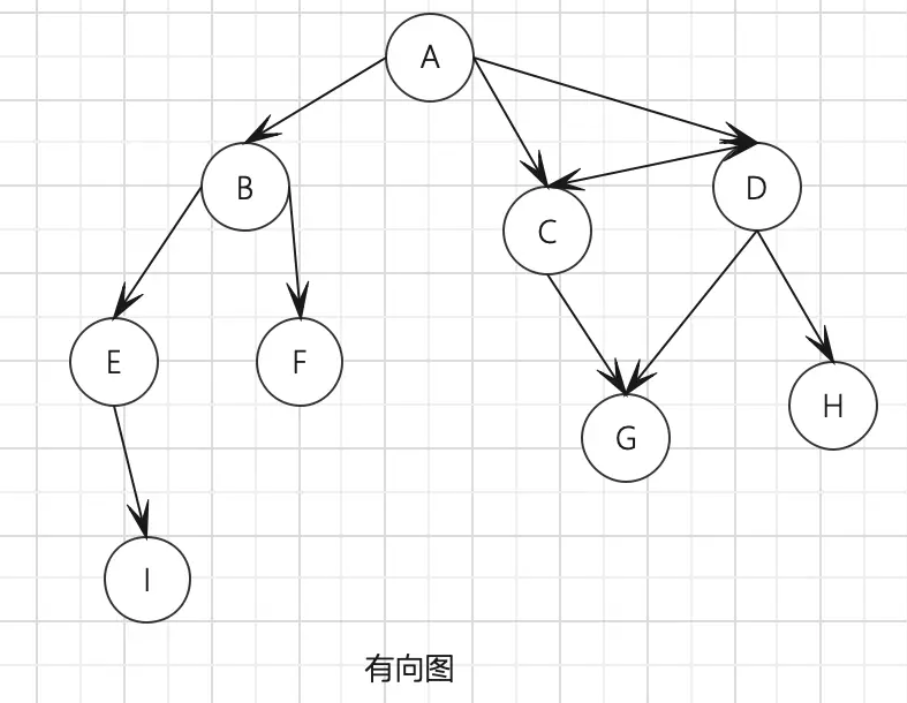
如果图中每两个顶点间在双向上都存在路径，则该图是强连通的。如上图所示，C 和 D 是强连通的， 而 A 和 B 不是强连通的。

• 无向图：是指图的边没有方向。

图还可以是未加权的或是加权的。 如下图所示，加权图的边被赋予了权值。

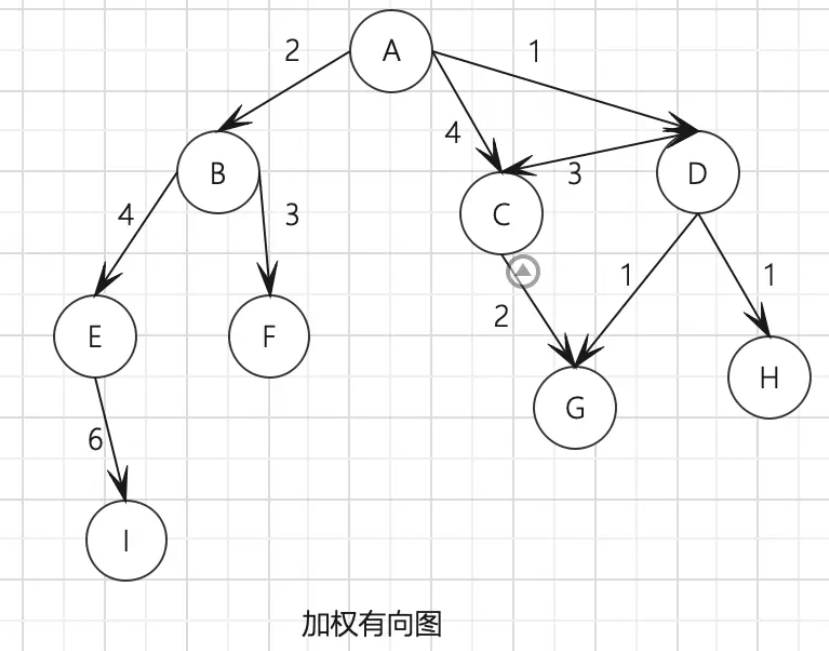
图的表示

从数据结构的角度来说，我们有多种方式来表示图。在所有的表示法中，不存在绝对正确的 方式。图的正确表示法取决于待解决的问题和图的类型。

• 邻接矩阵：图最常见的实现是邻接矩阵。每个节点都和一个整数相关联，该整数将作为数组的索引。我们用一个二维数组来表示顶点之间的连接。如果索引为 i 的节点和索引为 j 的节点相邻，则array[i][j] === 1，否则 array[i][j] === 0

不是强连通的图（稀疏图）如果用邻接矩阵来表示，则矩阵中将会有很多 0，这意味着我们 浪费了计算机存储空间来表示根本不存在的边。例如，找给定顶点的相邻顶点，即使该顶点只有 一个相邻顶点，我们也不得不迭代一整行。邻接矩阵表示法不够好的另一个理由是，图中顶点的 数量可能会改变，而二维数组不太灵活。

• 邻接表：我们也可以使用一种叫作邻接表的动态数据结构来表示图。邻接表由图中每个顶点的相邻顶点列表所组成。存在好几种方式来表示这种数据结构。我们可以用列表（数组）、链表，甚至是散列表或是字典来表示相邻顶点列表。

尽管邻接表可能对大多数问题来说都是更好的选择，但以上两种表示法都很有用，且它们有 着不同的性质（例如，要找出顶点 v 和 w 是否相邻，使用邻接矩阵会比较快）。

• 关联矩阵：还可以用关联矩阵来表示图。在关联矩阵中，矩阵的行表示顶点，列表示边。如下图所示，使用二维数组来表示两者之间的连通性，如果顶点 v 是边 e 的入射点，则 array[v][e] === 1；否则，array[v][e] === 0。 关联矩阵通常用于边的数量比顶点多的情况，以节省空间和内存。

图的表示方式

图结构通常有邻接矩阵和邻接表这 2 种表示方式。

邻接表

比如，现在有一组顶点和边的关系如下图所示：

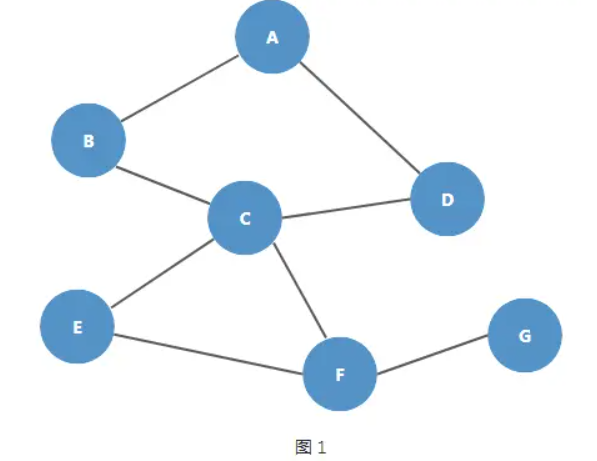
用邻接表来表示上示图结构如下：

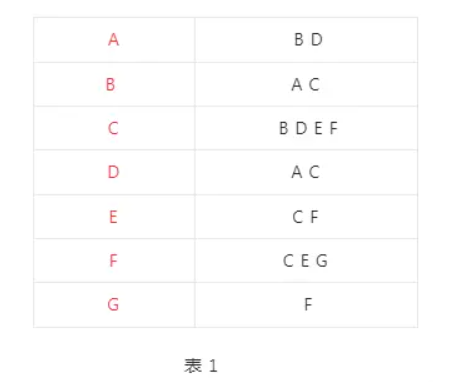
上表的每一行，之后都将是一个 Map 对象，第 1 列，也就是各个顶点，作为 key；第 2 列，也就是该顶点的相邻顶点（由一条边连接在一起的顶点）装入一个数组作为 value。

邻接表的优缺点

邻接表的优点在于计算出度（指向的其它顶点的数量）非常方便，顺便一提，某个顶点的度，等于其相邻顶点的数量； 缺点在于计算入度（本身被别的顶点指向的次数）就比较复杂了。

代码实现

整体框架

我们定义一个 Graph 类来实现图结构。图结构通常的特点也就是 Graph 应该包含的属性：

1. 有一组顶点，我们可以用数组 vertex 来装载所有的顶点；
2. 还有一组边，我们用 Map 对象 edge 来表示。

class Graph {
  constructor() {
    this.vertex = []; // 顶点
    this.edge = new Map(); // 边
  }
  // 下面添加方法
}

在图结构中，边是顶点和顶点之间的连线，它可以是有向的，比如顶点 A 和 B 之间有一条边，由 A 指向 B，那么从 A 可以通向 B，但是从 B 不能通向 A，我们就说这是一个有向图；也可以是无向的，也就是 A 和 B 之间的边并没有方向，A 可以通向 B，B 也能通向 A，那么我们就说这是一个无向图。上面图 1 所示，即为无向图，也是我们接下去要实现的图结构。

方法

添加顶点 addVertex()

添加顶点时要做 2 件事：

1. 将顶点放入保存顶点（v）的数组 vertex；
2. 在 edge 对象，也就是一个 Map 对象添加一个指定该顶点为键（key），值（value）为空数组的新键值对。

// 添加顶点
addVertex(v) {
  this.vertex.push(v)
  this.edge.set(v, [])
}

添加边 addEdge()

addEdge() 方法传入要添加的边的两端的顶点 v1 与 v2 作为参数，因为是无向图，所以我们要通过 Map.prototype.get() 方法获取这两个顶点为键所对应的值，也就是存储相邻顶点的数组，然后分别进行添加。

// 添加边
addEdge(v1, v2) {
  this.edge.get(v1).push(v2)
  this.edge.get(v2).push(v1)
}

P.S. 边除了之前说的可以有方向外，还可以有权重，比如表示地铁线路的图结构里，边的权重就可以表示站点与站点之间的票价或是所需时间，那么我们就说这是一个带权图。而像图 1 这样的，边不带任何意义的，即为无权图。

toString()

toString() {
  let tempString = ''
  for (let i = 0; i < this.vertex.length; i++) {
    tempString += this.vertex[i] + '===>'
    const tempArr = this.edge.get(this.vertex[i])
    for (let j = 0; j < tempArr.length; j++) {
      tempString += tempArr[j] + '\0'
    }
    tempString += '\n'
  }
  return tempString
}

toString 方法就是循环遍历每个顶点，在每次循环中，再循环遍历存储在 edge 里 key 为该顶点的 value，也就是各个顶点的相邻顶点组成的数组，然后进行字符串拼接。 下面按照图 1，进行顶点和边的添加，利用 toString() 方法对代码是否正确进行测试。

const graph = new Graph();
const vertexList = ["A", "B", "C", "D", "E", "F", "G"];
vertexList.forEach((v) => graph.addVertex(v));
graph.addEdge("A", "B");
graph.addEdge("A", "D");
graph.addEdge("B", "C");
graph.addEdge("C", "D");
graph.addEdge("C", "E");
graph.addEdge("C", "F");
graph.addEdge("E", "F");
graph.addEdge("F", "G");
console.log(graph.toString());

打印结果如下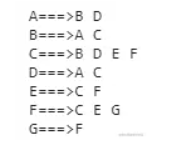： 与表 1 一致，说明目前为止代码的运行是符合预期的。

图的遍历

遍历图结构需要将图里的每一个顶点都访问一遍，并且不能重复。下面介绍 2 种遍历算法，它们都需要明确指定第一个被访问的顶点，即源顶点 s。另外，遍历过程会为顶点置色，以反映各个顶点的状态：

• 白色代表顶点未被访问；
• 黑色代表该顶点以及其所有相邻顶点都被访问过了；
• 灰色则代表该顶点被访问过，但其相邻顶点中还有未被访问过的白色顶点存在。

所以在最开始我们需要定义个初始化颜色的方法 initColor()，代码如下：

// 初始化颜色
initColor() {
  const colorMsg = {}
  this.vertex.forEach((v) => (colorMsg[v] = 'white'))
  return colorMsg
}

广度优先搜索（Breadth First Search, BFS）

又称广度优先搜索。从顶点 s 开始遍历，将顶点放入一个 队列 Q 中，并置灰，Q 中的顶点先被探索，即访问其所有相邻顶点。如果队列 Q 非空，则执行下列步骤：

1. 从队列取出一个顶点 v；
2. 访问其所有相邻顶点，将它们中未被访问过的白色顶点加入到 Q 中并置灰；
3. 将 v 置黑。

代码如下：

// 宽度优先搜索
bfs(v) {
  const colorMsg = this.initColor() // 将所有顶点的颜色初始化为白色
  const queue = new Queue()
  queue.push(v)
  while (!queue.isEmpty()) {
    const outVertex = queue.shift()
    const adjacentVertex = this.edge.get(outVertex)
    adjacentVertex.forEach((item) => {
      if (colorMsg[item] === 'white') {
        queue.push(item)
        colorMsg[item] = 'grey'
      }
    })
    colorMsg[outVertex] = 'black'
    console.log(outVertex)
  }
}

BFS 的特点就是先宽后深，一层层地访问各个顶点。遍历图 1 这样的结构顺序应该如下图所示：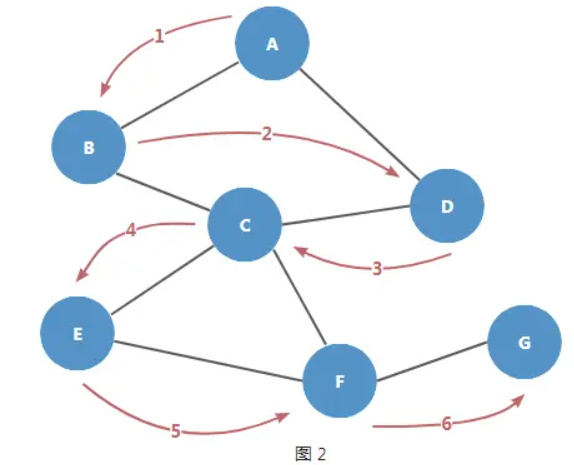

执行 graph.bfs('A') 进行测试，打印结果如下：

顺序符合图 2 的预期。

深度优先搜索（Depth First Search, DFS）

DFS 的实现可以基于栈或是使用递归，对每一个可能的分支路径深入到不能再深入为止，并且每个顶点只访问一次。以图 1 为例，步骤如下：

1. 最开始所有顶点依然为白色；
2. 从顶点 A 开始访问，之后访问 B，再访问 C，访问过的顶点置灰；
3. C 的相邻顶点有 D、E 和 F，因为添加顶点时先添加的是 D，所以先访问 D，D 之后没有顶点了，即 D 的所有相邻顶点都访问过了，将 D 置黑，再沿着原来的访问路径返回到顶点 C，判断 C 是否有未被访问的相邻顶点，发现有 E 和 F，则从 E 开始，再次进行深度优先遍历。图示如下：

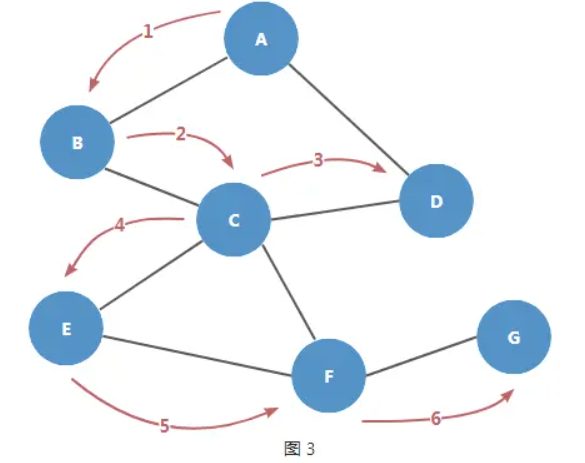
P.S. 所谓路径，就是由像图 1 中顶点 A、B、C、F 和 G 组成的连续序列。路径还可分为简单路径：不包含重复顶点； 和回路：第一个和最后一个顶点是同一个顶点的路径。

下面是使用递归实现的 DFS 方法，递归其实就是函数栈的调用：

// 深度优先搜索
dfs(v) {
  const colorMsg = this.initColor()
  this.dfsVisit(v, colorMsg)
}
// 递归方法
dfsVisit(v, colorMsg) {
  colorMsg[v] = 'grey'
  console.log(v)
  const adjacentVertex = this.edge.get(v)
  adjacentVertex.forEach((item) => {
    if (colorMsg[item] === 'white') {
      this.dfsVisit(item, colorMsg)
    }
  })
  colorMsg[v] = 'black'
}

时间和空间复杂度

基本理论

1. 时间复杂度

其实就是一个函数，用大 O 表示， 比如 O(1)、 O(n)...

它的作用就是用来定义描述算法的运行时间

• O(1)

let i = 0;
i += 1;

• O(n)： 如果是 O(1) + O(n) 则还是 O(n)

for (let i = 0; i < n; i += 1) {
  console.log(i);
}

• O(n^2)： O(n) * O(n), 也就是双层循环，自此类推： O(n^3)...

for (let i = 0; i < n; i += 1) {
  for (let j = 0; j < n; j += 1) {
    console.log(i, j);
  }
}

• O(logn)： 就是求 log 以 2 为底的多少次方等于 n

// 这个例子就是求2的多少次方会大于i，然后就会结束循环。 这就是一个典型的 O(logn)
let i = 1;
while (i < n) {
  console.log(i);
  i *= 2;
}

2. 空间复杂度

和时间复杂度一样，空间复杂度也是用大 O 表示，比如 O(1)、 O(n)...

它用来定义描述算法运行过程中临时占用的存储空间大小

占用越少 代码写的就越好

• O(1)： 单个变量，所以占用永远是 O(1)

let i = 0;
i += 1;

• O(n)： 声明一个数组， 添加 n 个值， 相当于占用了 n 个空间单元

const arr = [];
for (let i = 0; i < n; i += 1) {
  arr.push(i);
}

• O(n^2)： 类似一个矩阵的概念，就是二维数组的意思

const arr = [];
for (let i = 0; i < n; i += 1) {
  arr.push([]);
  for (let j = 0; j < n; j += 1) {
    arr[i].push(j);
  }
}

1. 什么是复杂度分析 ？

1. 数据结构和算法解决是 “如何让计算机更快时间、更省空间的解决问题”。
2. 因此需从执行时间和占用空间两个维度来评估数据结构和算法的性能。
3. 分别用时间复杂度和空间复杂度两个概念来描述性能问题，二者统称为复杂度。
4. 复杂度描述的是算法执行时间（或占用空间）与数据规模的增长关系。

2. 为什么要进行复杂度分析 ？

1. 和性能测试相比，复杂度分析有不依赖执行环境、成本低、效率高、易操作、指导性强的特点。
2. 掌握复杂度分析，将能编写出性能更优的代码，有利于降低系统开发和维护成本。

3. 如何进行复杂度分析 ？

3.1 大 O 表示法

算法的执行时间与每行代码的执行次数成正比，用 T(n) = O(f(n)) 表示，其中 T(n) 表示算法执行总时间，f(n) 表示每行代码执行总次数，而 n 往往表示数据的规模。这就是大 O 时间复杂度表示法。

3.2 时间复杂度

1）定义

算法的时间复杂度，也就是算法的时间量度。

大 O 时间复杂度表示法 实际上并不具体表示代码真正的执行时间，而是表示 代码执行时间随数据规模增长的变化趋势，所以也叫 渐进时间复杂度，简称 时间复杂度（asymptotic time complexity）。

例子 1：

function aFun() {
  console.log("Hello, World!"); //  需要执行 1 次
  return 0; // 需要执行 1 次
}

那么这个方法需要执行 2 次运算。

例子 2：

function bFun(n) {
  for (let i = 0; i < n; i++) {
    // 需要执行 (n + 1) 次
    console.log("Hello, World!"); // 需要执行 n 次
  }
  return 0; // 需要执行 1 次
}

那么这个方法需要执行 ( n + 1 + n + 1 ) = 2n +2 次运算。

例子 3：

function cal(n) {
  let sum = 0; // 1 次
  let i = 1; // 1 次
  let j = 1; // 1 次
  for (; i <= n; ++i) {
    // n 次
    j = 1; // n 次
    for (; j <= n; ++j) {
      // n * n ，也即是  n平方次
      sum = sum + i * j; // n * n ，也即是  n平方次
    }
  }
}

注意，这里是二层 for 循环，所以第二层执行的是 n * n = n2 次，而且这里的循环是 ++i，和例子 2 的是 i++，是不同的，是先加与后加的区别。

那么这个方法需要执行 ( n2 + n2 + n + n + 1 + 1 +1 ) = 2n2 +2n + 3 。

2）特点

以时间复杂度为例，由于 时间复杂度 描述的是算法执行时间与数据规模的 增长变化趋势，所以 常量、低阶、系数 实际上对这种增长趋势不产生决定性影响，所以在做时间复杂度分析时 忽略 这些项。

所以，上面例子 1 的时间复杂度为 T(n) = O(1)，例子 2 的时间复杂度为 T(n) = O(n)，例子 3 的时间复杂度为 T(n) = O(n2)。

3.3 时间复杂度分析

• 只关注循环执行次数最多的一段代码

单段代码看高频：比如循环。

function cal(n) {
  let sum = 0;
  let i = 1;
  for (; i <= n; ++i) {
    sum = sum + i;
  }
  return sum;
}

执行次数最多的是 for 循环及里面的代码，执行了 n 次，所以时间复杂度为 O(n)。

• 加法法则：总复杂度等于量级最大的那段代码的复杂度

多段代码取最大：比如一段代码中有单循环和多重循环，那么取多重循环的复杂度。

function cal(n) {
  let sum_1 = 0;
  let p = 1;
  for (; p < 100; ++p) {
    sum_1 = sum_1 + p;
  }

  let sum_2 = 0;
  let q = 1;
  for (; q < n; ++q) {
    sum_2 = sum_2 + q;
  }

  let sum_3 = 0;
  let i = 1;
  let j = 1;
  for (; i <= n; ++i) {
    j = 1;
    for (; j <= n; ++j) {
      sum_3 = sum_3 + i * j;
    }
  }

  return sum_1 + sum_2 + sum_3;
}

上面代码分为三部分，分别求 sum_1、sum_2、sum_3 ，主要看循环部分。

第一部分，求 sum_1 ，明确知道执行了 100 次，而和 n 的规模无关，是个常量的执行时间，不能反映增长变化趋势，所以时间复杂度为 O(1)。

第二和第三部分，求 sum_2 和 sum_3 ，时间复杂度是和 n 的规模有关的，为别为 O(n) 和 O(n2)。

所以，取三段代码的最大量级，上面例子的最终的时间复杂度为 O(n2)。

同理类推，如果有 3 层 for 循环，那么时间复杂度为 O(n3)，4 层就是 O(n4)。

所以，总的时间复杂度就等于量级最大的那段代码的时间复杂度。

• 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

嵌套代码求乘积：比如递归、多重循环等。

function cal(n) {
  let ret = 0;
  let i = 1;
  for (; i < n; ++i) {
    ret = ret + f(i); // 重点为  f(i)
  }
}

function f(n) {
  let sum = 0;
  let i = 1;
  for (; i < n; ++i) {
    sum = sum + i;
  }
  return sum;
}

方法 cal 循环里面调用 f 方法，而 f 方法里面也有循环。

所以，整个 cal() 函数的时间复杂度就是，T(n) = T1(n) T2(n) = O(nn) = O(n2) 。

• 多个规模求加法：比如方法有两个参数控制两个循环的次数，那么这时就取二者复杂度相加

function cal(m, n) {
  let sum_1 = 0;
  let i = 1;
  for (; i < m; ++i) {
    sum_1 = sum_1 + i;
  }

  let sum_2 = 0;
  let j = 1;
  for (; j < n; ++j) {
    sum_2 = sum_2 + j;
  }

  return sum_1 + sum_2;
}

以上代码也是求和 ，求 sum_1 的数据规模为 m、求 sum_2 的数据规模为 n，所以时间复杂度为 O(m+n)。

公式：T1(m) + T2(n) = O(f(m) + g(n)) 。

• 多个规模求乘法：比如方法有两个参数控制两个循环的次数，那么这时就取二者复杂度相乘

function cal(m, n) {
  let sum_3 = 0;
  let i = 1;
  let j = 1;
  for (; i <= m; ++i) {
    j = 1;
    for (; j <= n; ++j) {
      sum_3 = sum_3 + i * j;
    }
  }
}

以上代码也是求和，两层 for 循环 ，求 sum_3 的数据规模为 m 和 n，所以时间复杂度为 O(m*n)。

公式：T1(m) * T2(n) = O(f(m) * g(n)) 。

3.4 常用的时间复杂度分析

• 多项式阶：随着数据规模的增长，算法的执行时间和空间占用，按照多项式的比例增长。

包括 O(1)（常数阶）、O(logn)（对数阶）、O(n)（线性阶）、O(nlogn)（线性对数阶）、O(n2) （平方阶）、O(n3)（立方阶）。

除了 O(logn)、O(nlogn) ，其他的都可从上面的几个例子中看到。

下面举例说明 O(logn)（对数阶）：

let i = 1;
while (i <= n) {
  i = i * 2;
}

代码是从 1 开始，每次循环就乘以 2，当大于 n 时，循环结束。

其实就是高中学过的等比数列，i 的取值就是一个等比数列。在数学里面是这样子的：

20 21 22 ... 2k ... 2x = n

所以，我们只要知道 x 值是多少，就知道这行代码执行的次数了，通过 2x = n 求解 x，数学中求解得 x = log2n 。所以上面代码的时间复杂度为 O(log2n)。

实际上，不管是以 2 为底、以 3 为底，还是以 10 为底，我们可以把所有对数阶的时间复杂度都记为 O(logn)。为什么呢？

因为对数之间是可以互相转换的，log3n = log32 log2n，所以 O(log3n) = O(C log2n)，其中 C=log32 是一个常量。

由于 时间复杂度 描述的是算法执行时间与数据规模的 增长变化趋势，所以 常量、低阶、系数 实际上对这种增长趋势不产生决定性影响，所以在做时间复杂度分析时 忽略 这些项。

因此，在对数阶时间复杂度的表示方法里，我们忽略对数的 “底”，统一表示为 O(logn)。

下面举例说明 O(nlogn)（对数阶）：

function aFun(n) {
  let i = 1;
  while (i <= n) {
    i = i * 2;
  }
  return i;
}

function cal(n) {
  let sum = 0;
  for (let i = 1; i <= n; ++i) {
    sum = sum + aFun(n);
  }
  return sum;
}

aFun 的时间复杂度为 O(logn)，而 cal 的时间复杂度为 O(n)，所以上面代码的时间复杂度为 T(n) = T1(logn) T2(n) = O(lognn) = O(nlogn) 。

• 1. 非多项式阶：随着数据规模的增长，算法的执行时间和空间占用暴增，这类算法性能极差。

包括 O(2n)（指数阶）、O(n!)（阶乘阶）。

O(2n)（指数阶）例子：

aFunc( n ) {
    if (n <= 1) {
        return 1;
    } else {
        return aFunc(n - 1) + aFunc(n - 2);
    }
}

参考答案： 显然运行次数，T(0) = T(1) = 1，同时 T(n) = T(n - 1) + T(n - 2) + 1，这里的 1 是其中的加法算一次执行。 显然 T(n) = T(n - 1) + T(n - 2) 是一个斐波那契数列，通过归纳证明法可以证明，当 n >= 1 时 T(n) < (5/3)n，同时当 n > 4 时 T(n) >= (3/2)n。 所以该方法的时间复杂度可以表示为 O((5/3)n)，简化后为 O(2n)。 可见这个方法所需的运行时间是以指数的速度增长的。 如果大家感兴趣，可以试下分别用 1，10，100 的输入大小来测试下算法的运行时间，相信大家会感受到时间复杂度的无穷魅力。

3.5 时间复杂度分类

时间复杂度可以分为：

• 最好情况时间复杂度（best case time complexity）：在最理想的情况下，执行这段代码的时间复杂度。
• 最坏情况时间复杂度（worst case time complexity）：在最糟糕的情况下，执行这段代码的时间复杂度。
• 平均情况时间复杂度（average case time complexity），用代码在所有情况下执行的次数的加权平均值表示。也叫 加权平均时间复杂度 或者 期望时间复杂度。
• 均摊时间复杂度（amortized time complexity）: 在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。

举例说明：

// n 表示数组 array 的长度
function find(array, n, x) {
  let i = 0;
  let pos = -1;
  for (; i < n; ++i) {
    if (array[i] == x) {
      pos = i;
      break;
    }
  }
  return pos;
}

find 函数实现的功能是在一个数组中找到值等于 x 的项，并返回索引值，如果没找到就返回 -1 。

最好情况时间复杂度，最坏情况时间复杂度

如果数组中第一个值就等于 x，那么时间复杂度为 O(1)，如果数组中不存在变量 x，那我们就需要把整个数组都遍历一遍，时间复杂度就成了 O(n)。所以，不同的情况下，这段代码的时间复杂度是不一样的。

所以上面代码的 最好情况时间复杂度为 O(1)，最坏情况时间复杂度为 O(n)。

平均情况时间复杂度

如何分析平均时间复杂度 ？代码在不同情况下复杂度出现量级差别，则用代码所有可能情况下执行次数的加权平均值表示。

要查找的变量 x 在数组中的位置，有 n+1 种情况：在数组的 0 ～ n-1 位置中和不在数组中。我们把每种情况下，查找需要遍历的元素个数累加起来，然后再除以 n+1，就可以得到需要遍历的元素个数的平均值，即：

省略掉系数、低阶、常量，所以，这个公式简化之后，得到的平均时间复杂度就是 O(n)。

我们知道，要查找的变量 x，要么在数组里，要么就不在数组里。这两种情况对应的概率统计起来很麻烦，我们假设在数组中与不在数组中的概率都为 1/2。另外，要查找的数据出现在 0 ～ n-1 这 n 个位置的概率也是一样的，为 1/n。所以，根据概率乘法法则，要查找的数据出现在 0 ～ n-1 中任意位置的概率就是 1/(2n)。

因此，前面的推导过程中存在的最大问题就是，没有将各种情况发生的概率考虑进去。如果我们把每种情况发生的概率也考虑进去，那平均时间复杂度的计算过程就变成了这样：

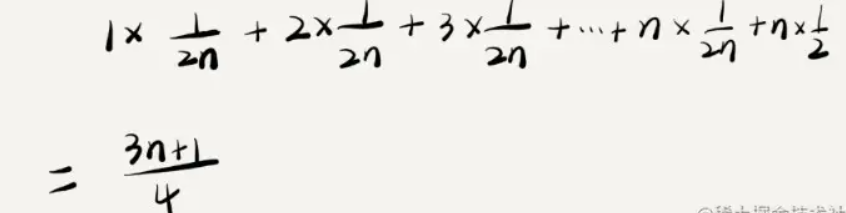
这个值就是概率论中的 加权平均值，也叫 期望值，所以平均时间复杂度的全称应该叫 加权平均时间复杂度 或者 期望时间复杂度。

所以，根据上面结论推导出，得到的 平均时间复杂度 仍然是 O(n)。

均摊时间复杂度

均摊时间复杂度就是一种特殊的平均时间复杂度 (应用场景非常特殊，非常有限，这里不说)。

3.6 时间复杂度总结

常用的时间复杂度所耗费的时间从小到大依次是：

O(1) < O(logn) < (n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

常见的时间复杂度：

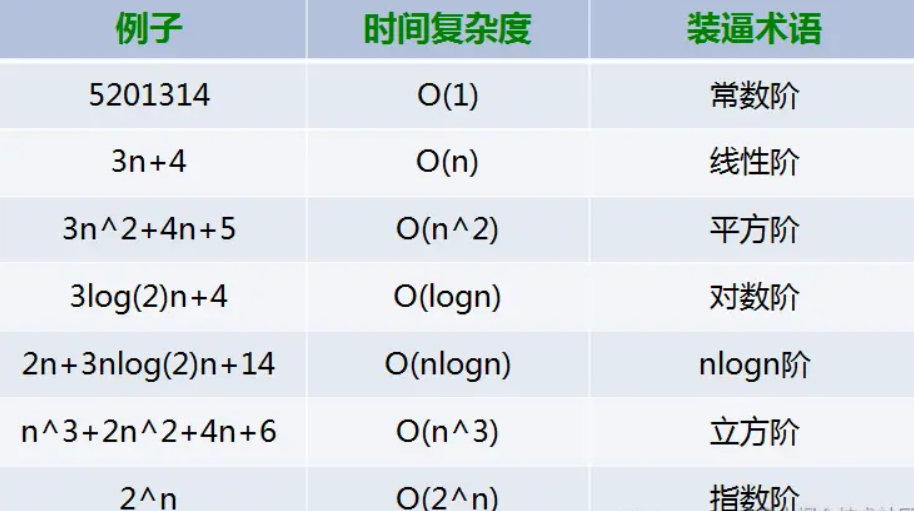
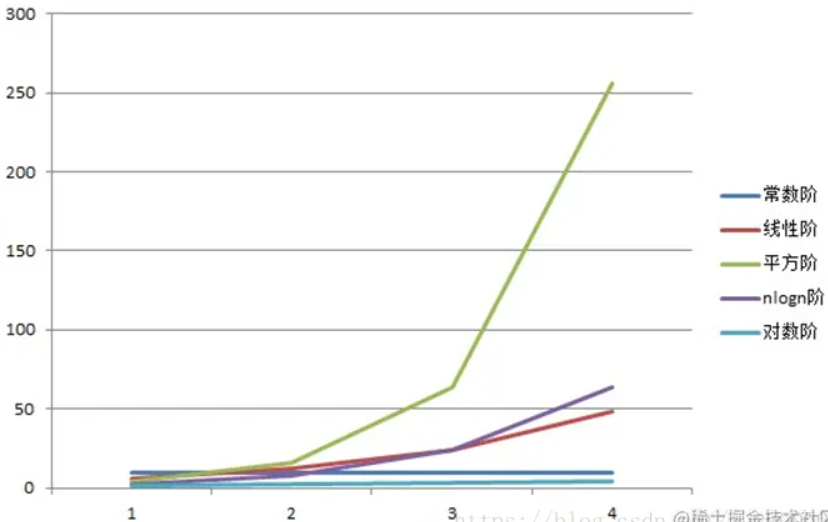
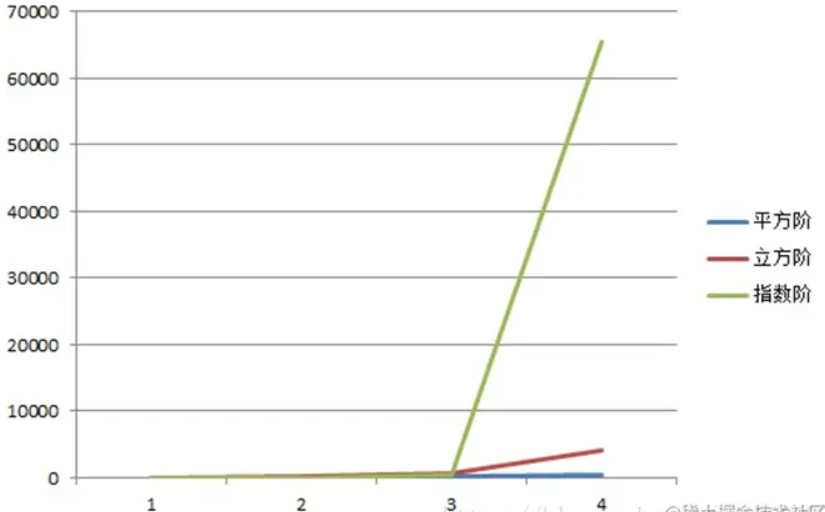
3.7 空间复杂度分析

时间复杂度的全称是 渐进时间复杂度，表示 算法的执行时间与数据规模之间的增长关系 。

类比一下，空间复杂度全称就是 渐进空间复杂度（asymptotic space complexity），表示 算法的存储空间与数据规模之间的增长关系 。

定义：算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式记作：S(n) = O(f(n))，其中，n 为问题的规模，f(n) 为语句关于 n 所占存储空间的函数。

function print(n) {
  const newArr = []; // 第 2 行
  newArr.length = n; // 第 3 行
  for (let i = 0; i < n; ++i) {
    newArr[i] = i * i;
  }

  for (let j = n - 1; j >= 0; --j) {
    console.log(newArr[i]);
  }
}

跟时间复杂度分析一样，我们可以看到，第 2 行代码中，我们申请了一个空间存储变量 newArr ，是个空数组。第 3 行把 newArr 的长度修改为 n 的长度的数组，每项的值为 undefined ，除此之外，剩下的代码都没有占用更多的空间，所以整段代码的空间复杂度就是 O(n)。

我们常见的空间复杂度就是 O(1)、O(n)、O(n2)，像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。

排序算法

十大经典排序算法总结（JavaScript 描述）

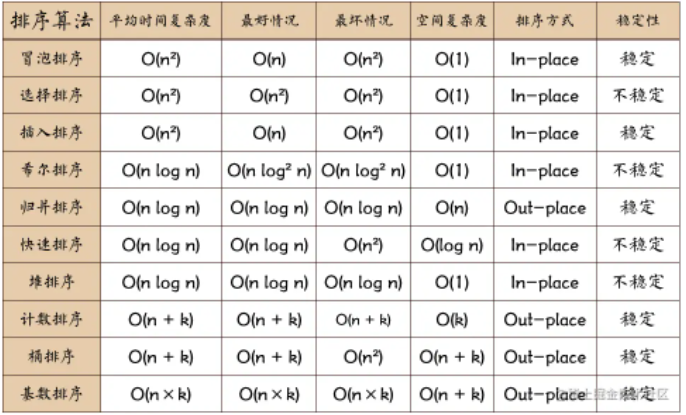
如何分析一个排序算法

复杂度分析是整个算法学习的精髓。

• 时间复杂度: 一个算法执行所耗费的时间。
• 空间复杂度: 运行完一个程序所需内存的大小。

学习排序算法，我们除了学习它的算法原理、代码实现之外，更重要的是要学会如何评价、分析一个排序算法。

分析一个排序算法，要从 执行效率、内存消耗、稳定性 三方面入手。

执行效率

1. 最好情况、最坏情况、平均情况时间复杂度

我们在分析排序算法的时间复杂度时，要分别给出最好情况、最坏情况、平均情况下的时间复杂度。 除此之外，你还要说出最好、最坏时间复杂度对应的要排序的原始数据是什么样的。

2. 时间复杂度的系数、常数 、低阶

我们知道，时间复杂度反应的是数据规模 n 很大的时候的一个增长趋势，所以它表示的时候会忽略系数、常数、低阶。

但是实际的软件开发中，我们排序的可能是 10 个、100 个、1000 个这样规模很小的数据，所以，在对同一阶时间复杂度的排序算法性能对比的时候，我们就要把系数、常数、低阶也考虑进来。

3. 比较次数和交换（或移动）次数

这一节和下一节讲的都是基于比较的排序算法。基于比较的排序算法的执行过程，会涉及两种操作，一种是元素比较大小，另一种是元素交换或移动。

所以，如果我们在分析排序算法的执行效率的时候，应该把比较次数和交换（或移动）次数也考虑进去。

内存消耗

也就是看空间复杂度。

还需要知道如下术语：

• 内排序：所有排序操作都在内存中完成；
• 外排序：由于数据太大，因此把数据放在磁盘中，而排序通过磁盘和内存的数据传输才能进行；
• 原地排序：原地排序算法，就是特指空间复杂度是 O(1) 的排序算法。

稳定性

• 稳定：如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序不变。 比如： a 原本在 b 前面，而 a = b，排序之后，a 仍然在 b 的前面；
• 不稳定：如果待排序的序列中存在值相等的元素，经过排序之后，相等元素之间原有的先后顺序改变。 比如：a 原本在 b 的前面，而 a = b，排序之后， a 在 b 的后面；

冒泡排序

一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来

思路如下：

• 比较相邻的元素，如果第一个比第二个大，就交换它们两个

• 对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对，这样在最后的元素应该会是最大的数

• 针对所有的元素重复以上的步骤，除了最后一个

• 重复上述步骤，直到没有任何一堆数字需要比较

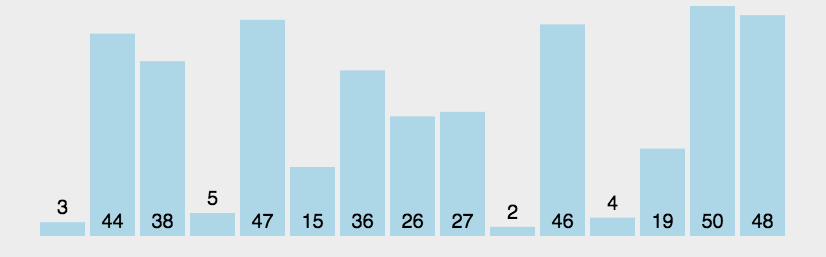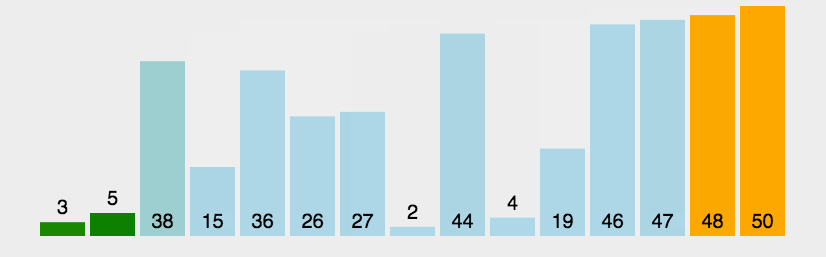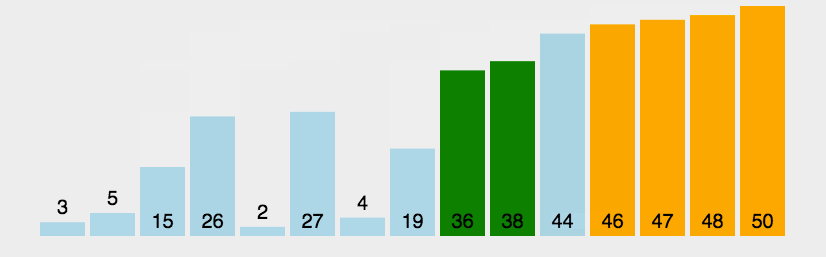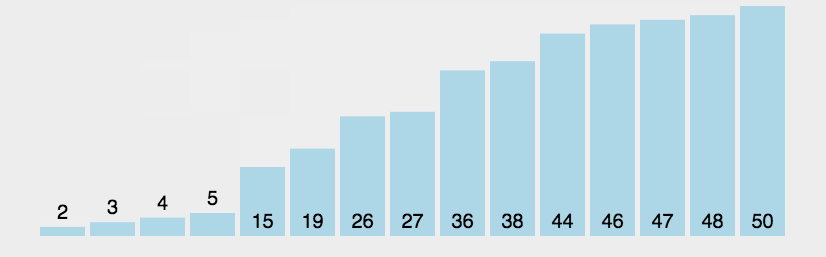
function bubbleSort1(arr) {
  const i = arr.length - 1; //初始时,最后位置保持不变
  while (i > 0) {
    let pos = 0; //每趟开始时,无记录交换
    for (let j = 0; j < i; j++) {
      if (arr[j] > arr[j + 1]) {
        let tmp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = tmp;
        pos = j; //记录最后交换的位置
      }
    }
    i = pos; //为下一趟排序作准备
  }
  return arr;
}

算法分析

• 最佳情况：T(n) = O(n)

• 最差情况：T(n) = O(n2)

• 平均情况：T(n) = O(n2)

选择排序

选择排序是一种简单直观的排序算法，它也是一种交换排序算法

无论什么数据进去都是 O(n²)的时间复杂度。所以用到它的时候，数据规模越小越好

唯一的好处是不占用额外的内存存储空间

思路如下：

• 在未排序序列中找到最小（大）元素，存放到排序序列的起始位置
• 从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
• 重复第二步，直到所有元素均排序完毕

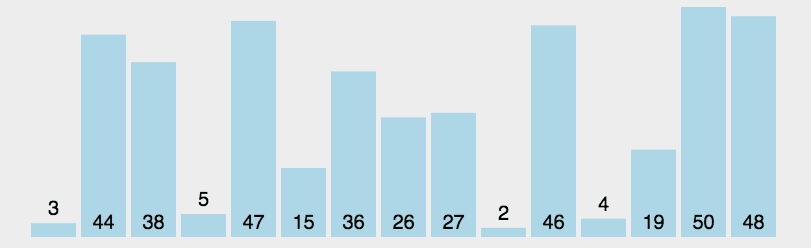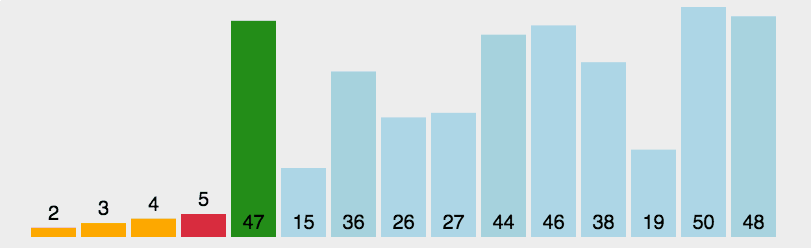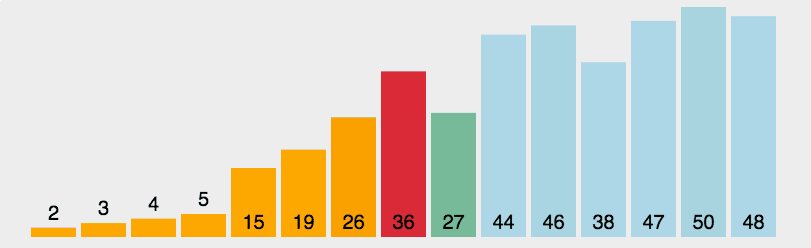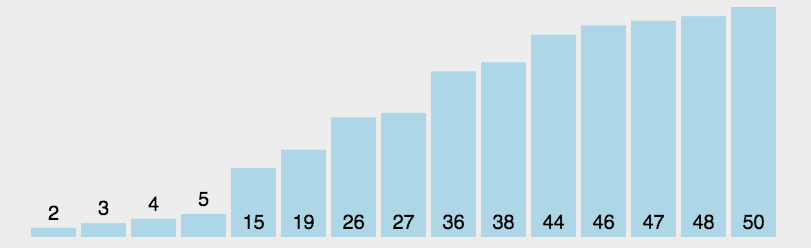
function selectionSort(arr) {
  var len = arr.length;
  var minIndex, temp;
  for (var i = 0; i < len - 1; i++) {
    minIndex = i;
    for (var j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) {
        // 寻找最小的数
        minIndex = j; // 将最小数的索引保存
      }
    }
    temp = arr[i];
    arr[i] = arr[minIndex];
    arr[minIndex] = temp;
  }
  return arr;
}

算法分析

• 最佳情况：T(n) = O(n2)
• 最差情况：T(n) = O(n2)
• 平均情况：T(n) = O(n2)

插入排序

插入排序是一种简单直观的排序算法

它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入

解决思路如下：

• 把待排序的数组分成已排序和未排序两部分，初始的时候把第一个元素认为是已排好序的
• 从第二个元素开始，在已排好序的子数组中寻找到该元素合适的位置并插入该位置（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）
• 重复上述过程直到最后一个元素被插入有序子数组中

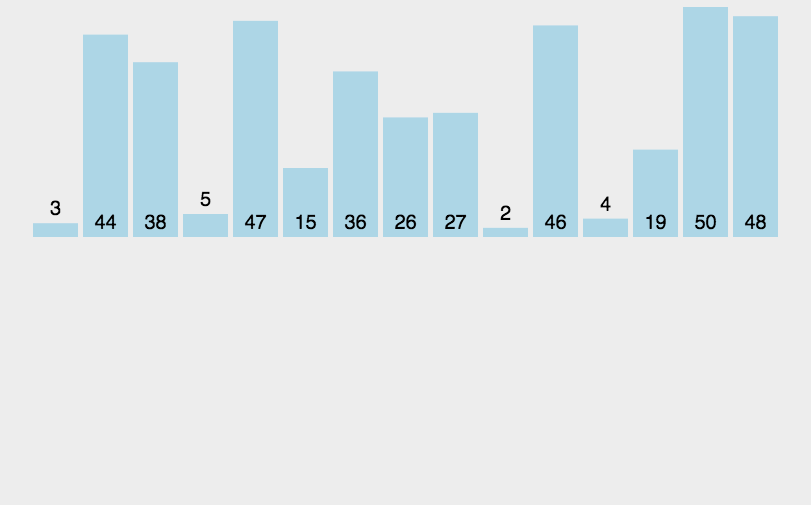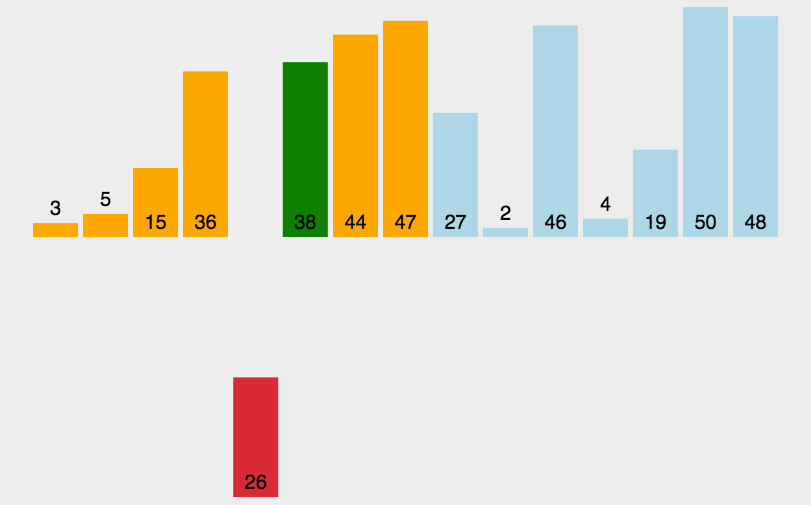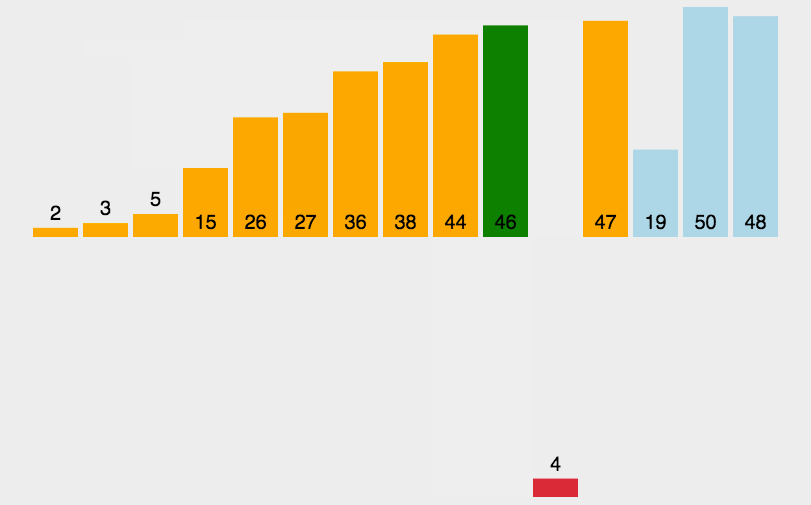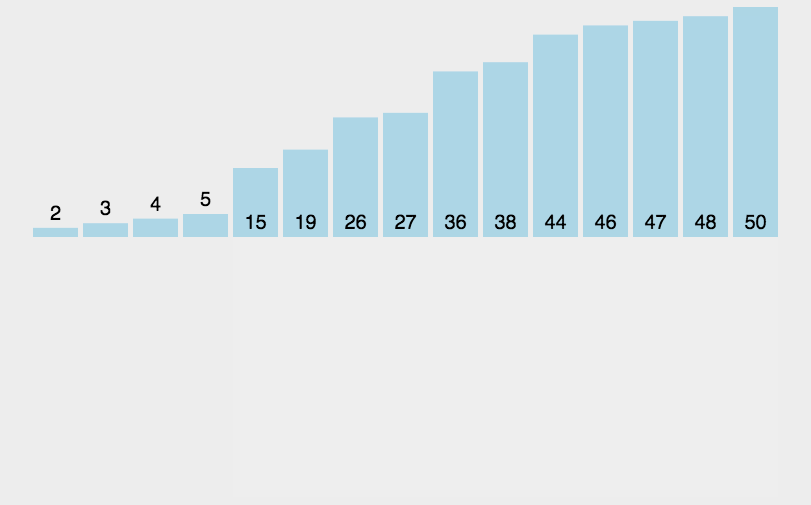
function insertionSort(arr) {
  const len = arr.length;
  let preIndex, current;
  for (let i = 1; i < len; i++) {
    preIndex = i - 1;
    current = arr[i];
    while (preIndex >= 0 && arr[preIndex] > current) {
      arr[preIndex + 1] = arr[preIndex];
      preIndex--;
    }
    arr[preIndex + 1] = current;
  }
  return arr;
}

算法分析

• 最佳情况：输入数组按升序排列。T(n) = O(n)
• 最坏情况：输入数组按降序排列。T(n) = O(n2)
• 平均情况：T(n) = O(n2)

希尔排序

1959 年 Shell 发明； 第一个突破 O(n^2)的排序算法；是简单插入排序的改进版；它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又叫缩小增量排序

希尔排序的核心在于间隔序列的设定。既可以提前设定好间隔序列，也可以动态的定义间隔序列。动态定义间隔序列的算法是《算法（第 4 版》的合著者 Robert Sedgewick 提出的。

算法描述

先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，具体算法描述：

• <1>. 选择一个增量序列 t1，t2，…，tk，其中 ti>tj，tk=1；
• <2>.按增量序列个数 k，对序列进行 k 趟排序；
• <3>.每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

function shellSort(arr) {
  var len = arr.length,
    temp,
    gap = 1;
  console.time("希尔排序耗时:");
  while (gap < len / 5) {
    //动态定义间隔序列
    gap = gap * 5 + 1;
  }
  for (gap; gap > 0; gap = Math.floor(gap / 5)) {
    for (var i = gap; i < len; i++) {
      temp = arr[i];
      for (var j = i - gap; j >= 0 && arr[j] > temp; j -= gap) {
        arr[j + gap] = arr[j];
      }
      arr[j + gap] = temp;
    }
  }
  console.timeEnd("希尔排序耗时:");
  return arr;
}
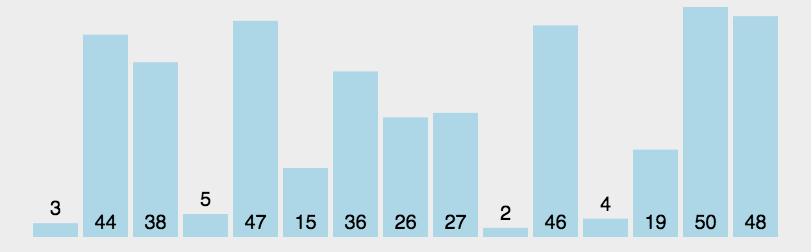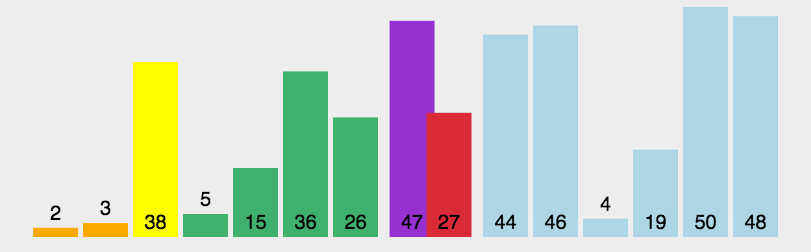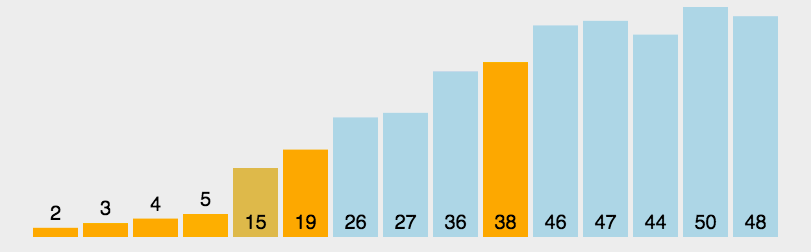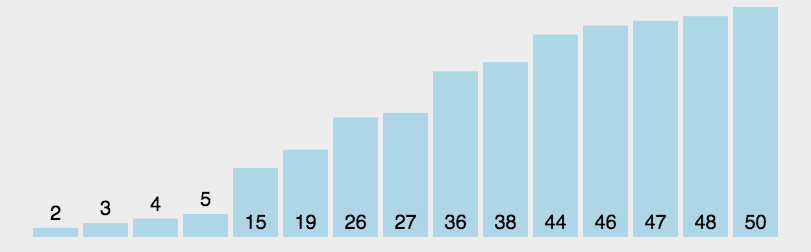
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(shellSort(arr)); //[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

希尔排序图示：

算法分析

• 最佳情况：T(n) = O(nlog2 n)
• 最坏情况：T(n) = O(nlog2 n)
• 平均情况：T(n) =O(nlog n)

归并排序

归并排序是建立在归并操作上的一种有效的排序算法

该算法是采用分治法的一个非常典型的应用

将已有序的子序列合并，得到完全有序的序列，即先使每个子序列有序，再使子序列段间有序

解决思路如下：

• 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
• 设定两个指针，最初位置分别为两个已经排序序列的起始位置
• 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
• 重复步骤 3 直到某一指针到达序列尾
• 将另一序列剩下的所有元素直接复制到合并序列尾

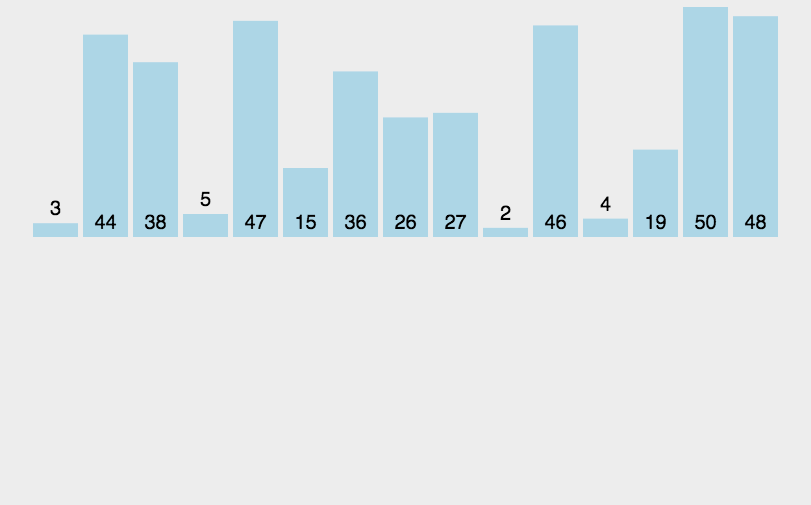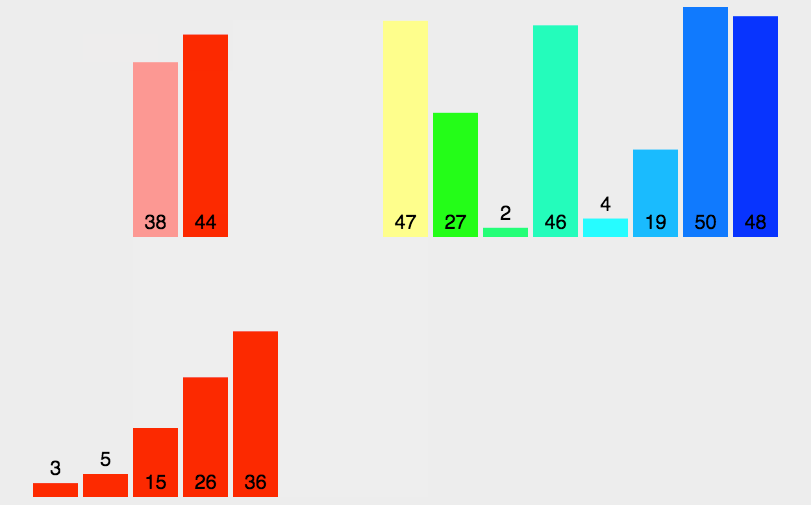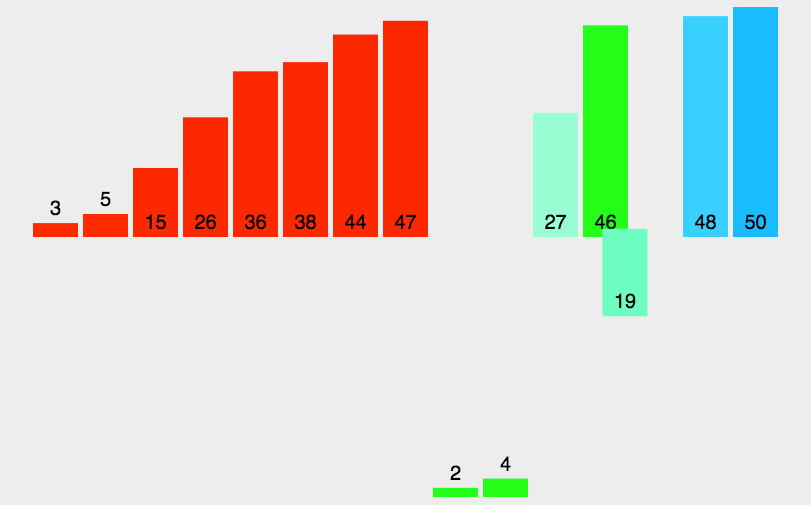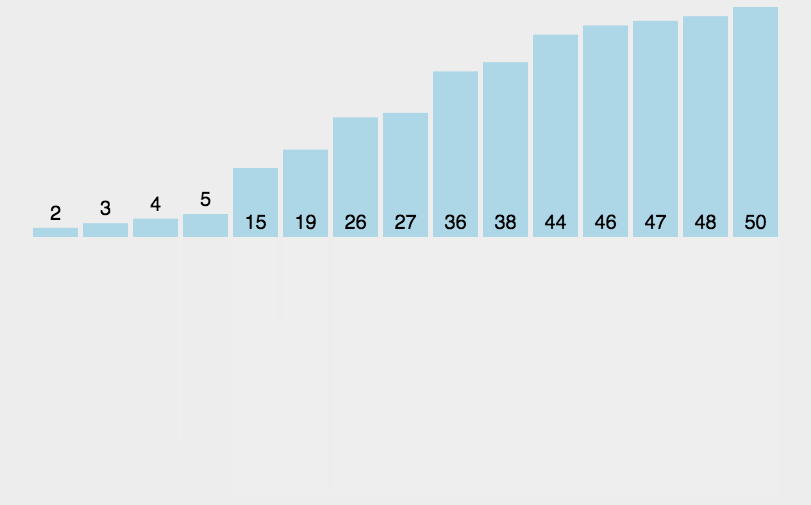
function mergeSort(arr) {
  // 采用自上而下的递归方法
  const len = arr.length;
  if (len < 2) {
    return arr;
  }
  let middle = Math.floor(len / 2),
    left = arr.slice(0, middle),
    right = arr.slice(middle);
  return merge(mergeSort(left), mergeSort(right));
}

function merge(left, right) {
  const result = [];

  while (left.length && right.length) {
    if (left[0] <= right[0]) {
      result.push(left.shift());
    } else {
      result.push(right.shift());
    }
  }

  while (left.length) result.push(left.shift());

  while (right.length) result.push(right.shift());

  return result;
}

算法分析

• 最佳情况：T(n) = O(n)
• 最差情况：T(n) = O(nlogn)
• 平均情况：T(n) = O(nlogn)

快速排序

快速排序是对冒泡排序算法的一种改进，基本思想是通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据比另一部分的所有数据要小

再按这种方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，使整个数据变成有序序列

解决思路如下：

• 从数列中挑出一个元素，称为"基准"（pivot）
• 重新排序数列，所有比基准值小的元素摆放在基准前面，所有比基准值大的元素摆在基准后面（相同的数可以到任何一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作
• 递归地（recursively）把小于基准值元素的子数列和大于基准值元素的子数列排序

function quickSort(arr) {
  const rec = (arr) => {
    if (arr.length <= 1) {
      return arr;
    }
    const left = [];
    const right = [];
    const mid = arr[0]; // 基准元素
    for (let i = 1; i < arr.length; i++) {
      if (arr[i] < mid) {
        left.push(arr[i]);
      } else {
        right.push(arr[i]);
      }
    }
    return [...rec(left), mid, ...rec(right)];
  };
  return res(arr);
}

算法分析

• 最佳情况：T(n) = O(nlogn)
• 最差情况：T(n) = O(n2)
• 平均情况：T(n) = O(nlogn)

堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。堆排序可以说是一种利用堆的概念来排序的选择排序。分为两种方法：

• 大顶堆：每个节点的值都大于或等于其子节点的值，在堆排序算法中用于升序排列；大顶堆的一个特性是数据将被从大到小取出，将取出的数字按照相反的顺序进行排列，数字就完成了排序
• 小顶堆：每个节点的值都小于或等于其子节点的值，在堆排序算法中用于降序排列；

堆排序的平均时间复杂度为 Ο(nlogn)。

算法步骤

堆排序的基本思想是：

1、将带排序的序列构造成一个大顶堆，根据大顶堆的性质，当前堆的根节点（堆顶）就是序列中最大的元素；

2、将堆顶元素和数组最后一个元素交换，然后将剩下的节点重新构造成一个大顶堆；

3、重复步骤 2，如此反复，从第一次构建大顶堆开始，每一次构建，我们都能获得一个序列的最大值，然后把它放到大顶堆的尾部。最后，就得到一个有序的序列了。

• 将初始待排序关键字序列(R1,R2....Rn)构建成大顶堆，此堆为初始的无序区；
• 将堆顶元素 R[1]与最后一个元素 R[n]交换，此时得到新的无序区(R1,R2,......Rn-1)和新的有序区(Rn),且满足 R[1,2...n-1]<=R[n]；
• 由于交换后新的堆顶 R[1]可能违反堆的性质，因此需要对当前无序区(R1,R2,......Rn-1)调整为新堆，然后再次将 R[1]与无序区最后一个元素交换，得到新的无序区(R1,R2....Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为 n-1，则整个排序过程完成。

var len;
function buildMaxHeap(arr) {
  //建立大顶堆
  len = arr.length; //第一个非叶子结点的下标为i=Math.floor(arr.length/2 - 1)
  for (var i = Math.floor(len / 2); i >= 0; i--) {
    heapify(arr, i); //下标 i 依次减1（即从第一个非叶子结点开始，从右至左，从下至上遍历所有非叶子节点）
  }
}
function heapify(arr, i) {
  //调整堆 以三个数为基础进行比较 父节点 左子节点 右子节点
  let left = 2 * i + 1, //对于结点 i ，其子结点为 2*i+1 与 2*i+2
    right = 2 * i + 2,
    largest = i;
  if (left < len && arr[left] > arr[largest]) {
    largest = left;
  }
  if (right < len && arr[right] > arr[largest]) {
    largest = right;
  }
  if (largest != i) {
    swap(arr, i, largest);
    heapify(arr, largest);
  }
}
function swap(arr, i, j) {
  var temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}
function heapSort(arr) {
  buildMaxHeap(arr);
  for (var i = arr.length - 1; i > 0; i--) {
    swap(arr, 0, i);
    len--;
    heapify(arr, 0);
  }
  return arr;
}

var arr = [1, 3, 0, 5, 2, 9, 10, 11, 4];
console.log(heapSort(arr));

算法分析

• 最佳情况：T(n) = O(nlogn)
• 最差情况：T(n) = O(nlogn)
• 平均情况：T(n) = O(nlogn)

计数排序

计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组 C，其中第 i 个元素是待排序数组 A 中值等于 i 的元素的个数。然后根据数组 C 来将 A 中的元素排到正确的位置。它只能对整数进行排序。

具体算法描述如下：

• 找出待排序的数组中最大和最小的元素；
• 统计数组中每个值为 i 的元素出现的次数，存入数组 C 的第 i 项；
• 对所有的计数累加（从 C 中的第一个元素开始，每一项和前一项相加）；
• 反向填充目标数组：将每个元素 i 放在新数组的第 C(i)项，每放一个元素就将 C(i)减去 1。

function countingSort(array) {
  var len = array.length,
    B = [],
    C = [],
    min = (max = array[0]);
  console.time("计数排序耗时");
  for (var i = 0; i < len; i++) {
    min = min <= array[i] ? min : array[i];
    max = max >= array[i] ? max : array[i];
    C[array[i]] = C[array[i]] ? C[array[i]] + 1 : 1;
  }
  for (var j = min; j < max; j++) {
    C[j + 1] = (C[j + 1] || 0) + (C[j] || 0);
  }
  for (var k = len - 1; k >= 0; k--) {
    B[C[array[k]] - 1] = array[k];
    C[array[k]]--;
  }
  console.timeEnd("计数排序耗时");
  return B;
}
var arr = [2, 2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];
console.log(countingSort(arr)); //[1, 1, 2, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]

JavaScript 动图演示：

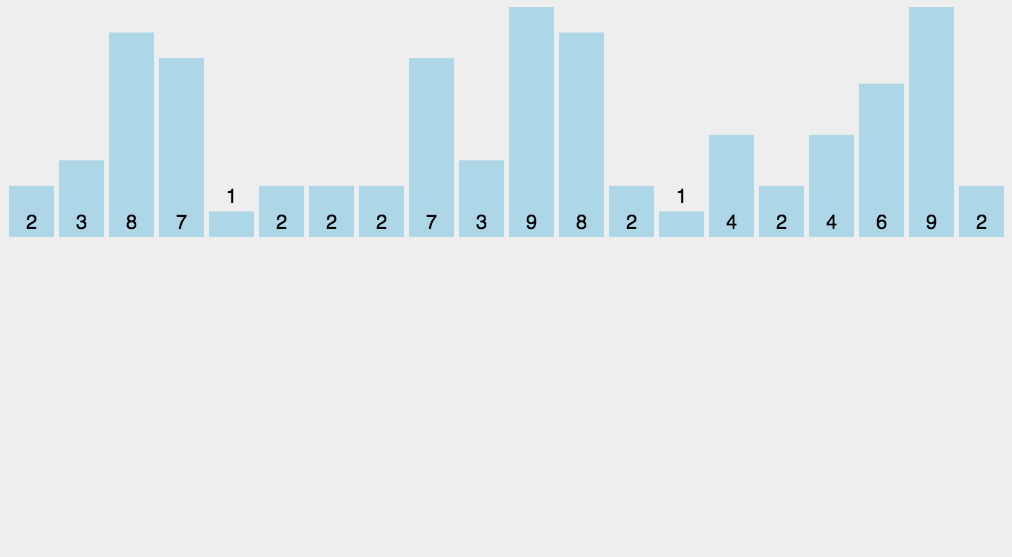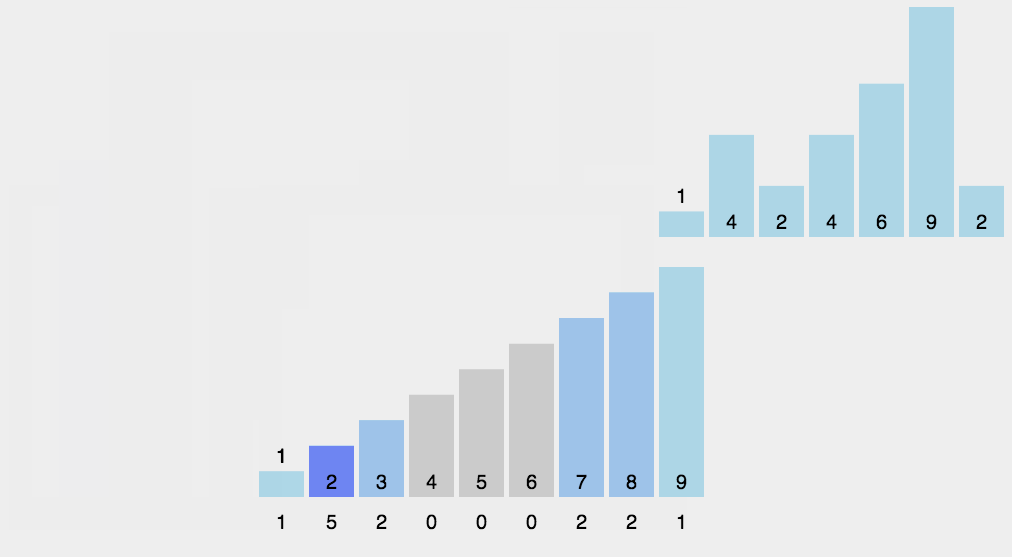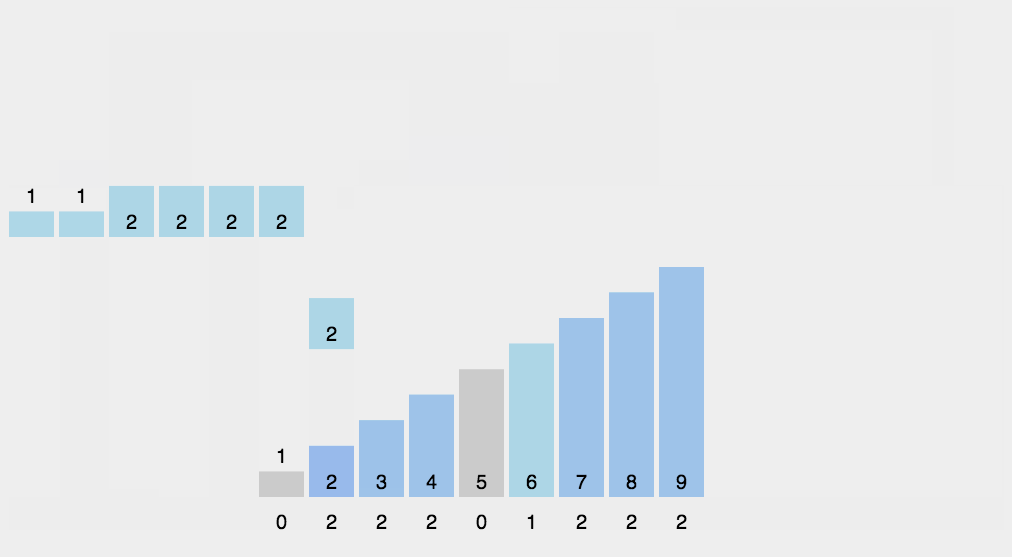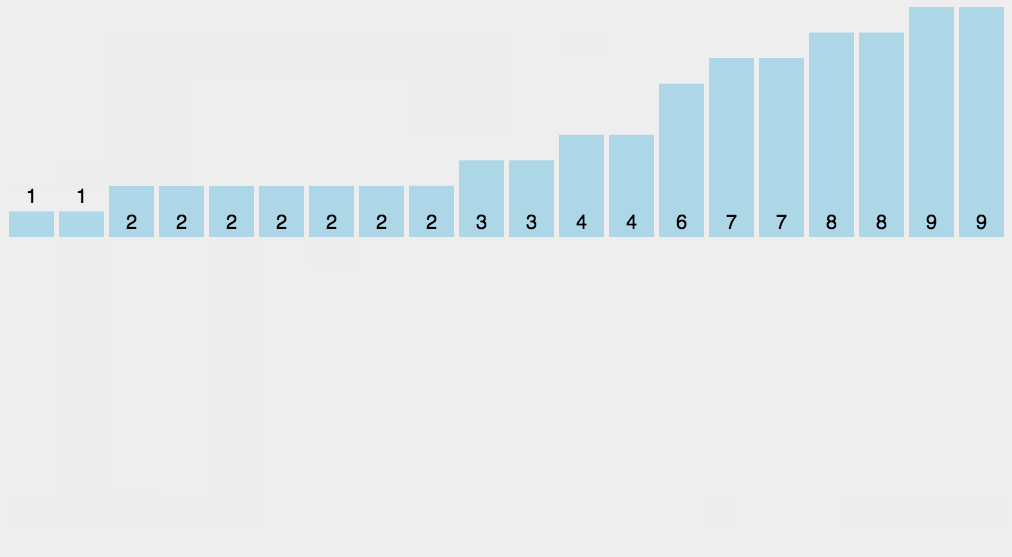
算法分析

当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 O(n + k)。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组 C 的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上 1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。

• 最佳情况：T(n) = O(n+k)
• 最差情况：T(n) = O(n+k)
• 平均情况：T(n) = O(n+k)

桶排序

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于这个映射函数的确定。

桶排序 (Bucket sort)的工作的原理：假设输入数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归方式继续使用桶排序进行排

具体算法描述如下：

• 设置一个定量的数组当作空桶；
• 遍历输入数据，并且把数据一个一个放到对应的桶里去；
• 对每个不是空的桶进行排序；
• 从不是空的桶里把排好序的数据拼接起来。

Javascript 代码实现:

/*方法说明：桶排序
@param  array 数组
@param  num   桶的数量*/
function bucketSort(array, num) {
  if (array.length <= 1) {
    return array;
  }
  var len = array.length,
    buckets = [],
    result = [],
    min = (max = array[0]),
    regex = "/^[1-9]+[0-9]*$/",
    space,
    n = 0;
  num = num || (num > 1 && regex.test(num) ? num : 10);
  console.time("桶排序耗时");
  for (var i = 1; i < len; i++) {
    min = min <= array[i] ? min : array[i];
    max = max >= array[i] ? max : array[i];
  }
  space = (max - min + 1) / num;
  for (var j = 0; j < len; j++) {
    var index = Math.floor((array[j] - min) / space);
    if (buckets[index]) {
      //  非空桶，插入排序
      var k = buckets[index].length - 1;
      while (k >= 0 && buckets[index][k] > array[j]) {
        buckets[index][k + 1] = buckets[index][k];
        k--;
      }
      buckets[index][k + 1] = array[j];
    } else {
      //空桶，初始化
      buckets[index] = [];
      buckets[index].push(array[j]);
    }
  }
  while (n < num) {
    result = result.concat(buckets[n]);
    n++;
  }
  console.timeEnd("桶排序耗时");
  return result;
}
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(bucketSort(arr, 4)); //[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

桶排序图示（图片来源网络）：

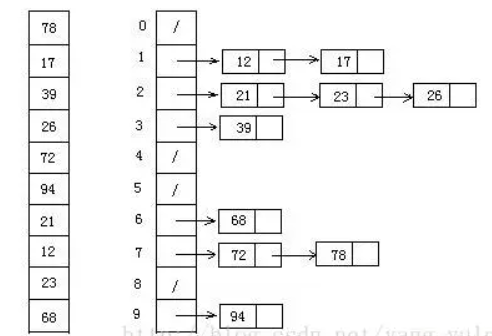
算法分析

桶排序最好情况下使用线性时间 O(n)，桶排序的时间复杂度，取决与对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为 O(n)。很显然，桶划分的越小，各个桶之间的数据越少，排序所用的时间也会越少。但相应的空间消耗就会增大。

• 最佳情况：T(n) = O(n+k)
• 最差情况：T(n) = O(n+k)
• 平均情况：T(n) = O(n2)

求数组相邻两数的最大差值

基数排序

基数排序也是非比较的排序算法，对每一位进行排序，从最低位开始排序，复杂度为 O(kn),为数组长度，k 为数组中的数的最大的位数；

基数排序是按照低位先排序，然后收集；再按照高位排序，然后再收集；依次类推，直到最高位。有时候有些属性是有优先级顺序的，先按低优先级排序，再按高优先级排序。最后的次序就是高优先级高的在前，高优先级相同的低优先级高的在前。基数排序基于分别排序，分别收集，所以是稳定的。

算法描述和实现

具体算法描述如下：

• 取得数组中的最大数，并取得位数；
• arr 为原始数组，从最低位开始取每个位组成 radix 数组；
• 对 radix 进行计数排序（利用计数排序适用于小范围数的特点）；

Javascript 代码实现：

/**
 * 基数排序适用于：
 *  (1)数据范围较小，建议在小于1000
 *  (2)每个数值都要大于等于0
 * @author xiazdong
 * @param  arr 待排序数组
 * @param  maxDigit 最大位数
 */
//LSD Radix Sort

function radixSort(arr, maxDigit) {
  var mod = 10;
  var dev = 1;
  var counter = [];
  console.time("基数排序耗时");
  for (var i = 0; i < maxDigit; i++, dev *= 10, mod *= 10) {
    for (var j = 0; j < arr.length; j++) {
      var bucket = parseInt((arr[j] % mod) / dev);
      if (counter[bucket] == null) {
        counter[bucket] = [];
      }
      counter[bucket].push(arr[j]);
    }
    var pos = 0;
    for (var j = 0; j < counter.length; j++) {
      var value = null;
      if (counter[j] != null) {
        while ((value = counter[j].shift()) != null) {
          arr[pos++] = value;
        }
      }
    }
  }
  console.timeEnd("基数排序耗时");
  return arr;
}
var arr = [3, 44, 38, 5, 47, 15, 36, 26, 27, 2, 46, 4, 19, 50, 48];
console.log(radixSort(arr, 2)); //[2, 3, 4, 5, 15, 19, 26, 27, 36, 38, 44, 46, 47, 48, 50]

基数排序 LSD 动图演示：

算法分析

• 最佳情况：T(n) = O(n * k)
• 最差情况：T(n) = O(n * k)
• 平均情况：T(n) = O(n * k)

基数排序有两种方法：

• MSD 从高位开始进行排序
• LSD 从低位开始进行排序

基数排序 vs 计数排序 vs 桶排序

这三种排序算法都利用了桶的概念，但对桶的使用方法上有明显差异：

1. 基数排序：根据键值的每位数字来分配桶
2. 计数排序：每个桶只存储单一键值
3. 桶排序：每个桶存储一定范围的数值

算法思想

位运算

平常我们用来计算的是十进制的数值 0~9 ，但是计算机是个机器，它只能识别二进制

根据国际 IEEE 754 标准，JavaScript 在存储数字时是始终以双精度浮点数来存储的，这种格式用 64 位二进制存储数值，64 位也就是 64 比特（bit），相当于 8 个字节，其中 0 到 51 存储数字（片段），52 到 62 存储指数，63 位存储符号

而在 JS 位运算中，并不会用 64 位来计算，它会先在后台把值转换为 32 位数值，再进行位运算操作，位运算计算完成后再将 32 位转为 64 位存储，整个过程就像在处理 32 位数值一样，所以我们了解位运算时，只需要关注这 32 位二进制整数就可以，因为 64 位存储格式是不可见的，但是也正是因为后台这个默认转换操作，给 JS 这门语言产生了一个副作用，即特殊值 NaN 和 Infinity 在位运算中都会直接被当作 0 来处理

ECMAScript 整数有两种类型，即有符号整数（允许用正数和负数）和无符号整数（只允许用正数）

在 ECMAScript 中，所有整数字面量默认都是有符号整数

有符号整数也就是上文所说，二进制左侧首位是符号位来表明该数字正负

而无符号整数就是没有符号位，没有了符号位置也就说它表达不了负数，同时因为没有了符号位置，它的存储范围也会比有符号整数存储范围大

位运算符有 7 个，分为两类：

• 逻辑位运算符：位与（&）、位或（|）、位异或（^）、非位（~）
• 移位运算符：左移（<<）、右移（>>）、无符号右移（>>>）

逻辑位运算符与逻辑运算符的运算方式是相同的，但是针对的对象不同。逻辑位运算符针对的是二进制的整数值，而逻辑运算符针对的是非二进制的值。

“&”运算符

“&”运算符（位与）用于对两个二进制操作数逐位进行比较，并根据下表所示的换算表返回结果。

第一个数的位值	第二个数的位值	运算结果
1	1	1
1	0	0
0	1	0
0	0	0

在位运算中，数值 1 表示 true，0 表示 false，反之亦然。

12 和 5 进行位与运算，则返回值为 4。

console.log(12 & 5); //返回值4

下图以算式的形式解析了 12 和 5 进行位与运算的过程。通过位与运算，只有第 3 位的值为全为 true，故返回 true，其他位均返回 false。

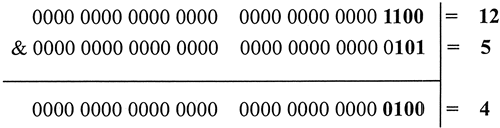
使用按位与 & 判断奇偶数

按位与这个东西平常用的不太多，我一般只会在判断奇偶数的才会用到，如下：

偶数 & 1; // 0
奇数 & 1; // 1

因为十进制数字 1 的二进制为 0000 ... 0001，只有最后一位为 1，其余位都是 0 ，所以任何数字和它对比除最后一位其余都是 0，那么当这个数字末位为 1 时，也就是奇数，那么结果就是 1，这个数字末位为 0 时，也就是偶数，那么结果就是 0，毕竟二进制只有 0 和 1

使用按位与 & 判断数字是否为 2 的整数幂

判断数字是否为 2 的整数幂，使用 n & (n - 1)

let a = 20;
let b = 32;

a & (a - 1); // 16 a不是2的整数幂
b & (b - 1); // 0   b是2的整数幂

如上所示，套用这个小公式，当结果等于 0 时，数值就是 2 的整数幂

其实原理也很简单，首先我们来看数值 2 的幂对应的二进制

0000 0001  -> 1     // 2^0
0000 0010  -> 2     // 2^1
0000 0100  -> 4     // 2^2
0000 1000  -> 8     // 2^3
0001 0000  -> 16    // 2^4

如上，2 的幂在二进制中只有一个 1 后跟一些 0，那么我们在判断一个数字是不是 2 的幂时，用 n & (n-1)，如果 你是 2 的幂，n 减 1 之后的二进制就是原来的那一位 1 变成 0，后面的 0 全变成 1，这个时候再和自身做按位与对比时，每一位都不同，所以每一位都是 0，即最终结果为 0

“|”运算符

“|”运算符（位或）用于对两个二进制操作数逐位进行比较，并根据如表格所示的换算表返回结果。

第一个数的位值	第二个数的位值	运算结果
1	1	1
1	0	1
0	1	1
0	0	0

12 和 5 进行位或运算，则返回值为 13。

console.log(12 | 5); //返回值13

下图以算式的形式解析了 12 和 5 进行位或运算的过程。通过位或运算，除第 2 位的值为 false 外，其他位均返回 true。

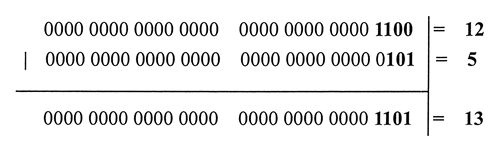
使用按位或 ｜ 取整

取整的时候我们也可以使用按位或取整

1.111 | 0; // 1
2.234 | 0; // 2

如上所示，只需要将小数同 0 进行按位或运算即可

原理也简单，位运算操作的是整数，相当于数值的整数部分和 0 进行按位或运算

0 的二进制全是 0 ，按位或对比时 1 和 0 就是 1 ，0 和 0 就是 0，得出的二进制就是我们要取整数值的整数部分

使用按位或 | 代替 Math.round()

我们上面知道按位或可以取整，其实四舍五入也就那么回事了，即正数加 0.5，负数减 0.5 进行按位或取整即可，道理就是这么简单，如下

let a1 = 1.1;
let a2 = 1.6;
(a1 + 0.5) | 0; // 1
(a2 + 0.5) | 0; // 2

let b1 = -1.1;
let b2 = -1.6;
(b1 - 0.5) | 0; // -1
(b2 - 0.5) | 0; // -2

“^”运算符

“^”运算符（位异或）用于对两个二进制操作数逐位进行比较，并根据如表格所示的换算表返回结果。

第一个数的位值	第二个数的位值	运算结果
1	1	0
1	0	1
0	1	1
0	0	0

12 和 5 进行位异或运算，则返回值为 9。

console.log(12 ^ 5); //返回值9

下图以算式的形式解析了 12 和 5 进行位异或运算的过程。通过位异或运算，第 1、4 位的值为 true，而第 2、3 位的值为 false。

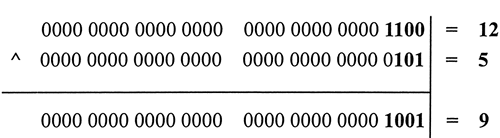
使用按位异或 ^ 判断整数部分是否相等

按位异或可以用来判断两个整数是否相等，如下

let a = 1;
let b = 1;
a ^ b; // 0

1 ^ 1; // 0
2 ^ 2; // 0
3 ^ 3; // 0

这是因为按位异或只在一位是 1 时返回 1，两位都是 1 或者两位都是 0 都返回 0，两个相同的数字二进制都是一致的，所以都是 0

我们也可以用作判断两个小数的整数部分是否相等，如下

2.1 ^ 2.5; // 0
2.2 ^ 2.6; // 0
2.1 ^ 3.1; // 1

这是为什么？牢记位运算操作的是整数、是整数、是整数，也就是说上面这几个对比完全可以理解为同下

2 ^ 2; // 0
2 ^ 2; // 0
2 ^ 3; // 1

使用按位异或 ^ 来完成值交换

我们也可以使用按位异或来进行两个变量的值交换，如下

let a = 1;
let b = 2;
a ^= b;
b ^= a;
a ^= b;
console.log(a); // 2
console.log(b); // 1

道理也很简单，我们先要了解一个东西

// 如果
a ^ b = c
// 那么
c ^ b = a
c ^ a = b

现在你再品一下值交换为什么可以交换，细品

不过这里使用 ^ 来做值交换不如用 ES6 的解构，因为 ES6 解构更方便易懂

使用按位异或 ^ 切换 0 和 1

切换 0 和 1，即当变量等于 0 时，将它变成 1，当变量等于 1 时，将它变成 0

常用于 toggle 开关状态切换，做开关状态更改时，普通小伙伴会如下这样做

let toggle = 0;

if (toggle) {
  toggle = 0;
} else {
  toggle = 1;
}

聪明点的小伙伴会用三目运算符

let toggle = 0;

toggle = toggle ? 0 : 1;

使用按位异或更简单

let toggle = 0;

toggle ^= 1;

原理也简单， toggle ^= 1 等同于 toggle = toggle ^ 1，我们知道 0 ^ 1 等于 1，而 1 ^ 1 则为 0

使用按位异或 ^ 判断两数符号是否相同

我们可以使用 (a ^ b) >= 0 来判断两个数字符号是否相同，也就是说同为正或同为负

let a = 1;
let b = 2;
let c =
  -2(a ^ b) >=
  0(
    // true
    a ^ c
  ) >=
  0; // false

原理也简单，正数二进制左首位也就是符号位是 0，而负数则是 1

按位异或在对比时，只有一正一负时才为 1，两位都是 0 或者都是 1 时结果为 0

所以，两个数值符号一样时按位异或对比后的二进制结果符号位肯定是 0，最终数值也就是 >=0，反之则 <0

“~”运算符

“~”运算符（位非）用于对一个二进制操作数逐位进行取反操作。

• 第 1 步：把运算数转换为 32 位的二进制整数。
• 第 2 步：逐位进行取反操作。
• 第 3 步：把二进制反码转换为十进制浮点数。

反码是符号位不变其余位置取反，而按位非则是取反码后符号位也取反

对 12 进行位非运算，则返回值为 -13。

console.log(~12); //返回值-13

下图以算式的形式解析了对 12 进行位非运算的过程。

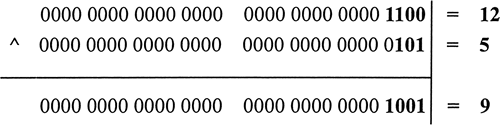
位非运算实际上就是对数字进行取负运算，再减 1。例如：

console.log( ~ 12 == 12-1);  //返回true

和 (-x) - 1 是一致的，那么为什么还要用按位非呢

很简单，原因有二，第一是位运算的操作是在数值底层表示上完成的，速度快。第二是因为它只用 2 个字符，比较方便

使用按位非 ~ 判断是否等于-1

let str = "abcdefg";

if (!~str.indexOf("n")) {
  console.log("字符串 str 中不存在字符 n");
}

// 等同于

if (str.indexOf("n") == "-1") {
  console.log("字符串 str 中不存在字符 n");
}

indexOf方法在找不到相同值时返回 -1，而~-1 == 0 == false，所以!~-1 == 1 == true

使用按位非 ~ 取整

按位非的骚操作中，还有一个比较普遍的就是位运算双非取整了，如下所示

~~3.14 == 3;

很多人知道这样可以取整，但是由于不知道具体是为什么而不敢用，所以我们来解释下为什么它为什么可以取整

上面我们说过，在 JS 位运算中，并不会用 64 位来计算，它会先在后台把值转换为 32 位整数，再进行位运算操作，位运算计算完成后再将 32 位转为 64 位存储，整个过程就像在处理 32 位数值一样，所以我们了解位运算时，只需要关注这 32 位二进制整数就可以

这里我们可以看到，32 位 整数，位运算操作的是整数，后台在进行 64 位到 32 位转换时，会忽略掉小数部分，只关注整数、整数、整数，记住了

~3.14 == ~3;
~5.89 == ~5;

如上所示，接着我们再按照上面的公式

~x == -x - 1;

((~~x == -(-x - 1) - 1) == -(-x) + 1 - 1) == x;

所以位运算中的双非 ~~ 即可取整，此取整是完全忽略小数部分

左移（<<）

简述

左移用符号 << 来表示，正如它的名字，即将数值的二进制码按照指定的位数向左移动，符号位不变

例如：

求 2 << 5，即求十进制数 2 左移 5 位的操作

我们先将十进制数字 2 转二进制再左移 5 位后如下图

我们得到了一个新的二进制，转为 10 进制即为数值 64

数字 x 左移 y 位我们其实可以得到一个公式，如下

x << y;

// 等同于

(x * 2) ^ y;

使用左移 << 取整

使用左移也可取整

1.111 << 0; // 1
2.344 << 0; // 2

原理是位运算操作的是整数，忽略小数部分，等同于数值的整数部分，左移 0 位，结果还是整数部分

有符号右移（>>）

简述

有符号右移用符号 >> 来表示，即将数值的二进制码按照指定的位数向右移动，符号位不变，它和左移相反

例如：

求 64 >> 5，即求十进制数 64 有符号右移 5 位的操作

我们先将十进制数字 64 转二进制再右移 5 位后如下图

有符号右移时移动数位后会同样也会造成空位，空位位于数字的左侧，但位于符号位之后，ECMAScript 中用符号位的值填充这些空位

随后，我们就得到了一个新的二进制，转为 10 进制即为数值 2，其实就是左移的逆运算

同样，数字 x 有符号右移 y 位我们也可以得到一个公式，如下

x >> y;

// 等同于

(x / 2) ^ y;

使用右移 >> 取整

使用右移和左移一样都可以取整

1.111 >> 0; // 1
2.344 >> 0; // 2

原理还是那一个，位运算操作的是整数，忽略小数部分，等同于数值的整数部分，右移 0 位，结果还是整数部分

无符号右移（>>>）

简述

无符号右移使用 >>> 表示，和有符号右移区别就是它是三个大于号，它会将数值的所有 32 位字符都右移

对于正数，无符号右移会给空位都补 0 ，不管符号位是什么，这样的话正数的有符号右移和无符号右移结果都是一致的

负数就不一样了，当把一个负数进行无符号右移时也就是说把负数的二进制码包括符号为全部右移，向右被移出的位被丢弃，左侧用 0 填充，由于符号位变成了 0，所以结果总是非负的

那么可能就有人要问了，如果一个负数无符号右移 0 位呢，我们可以测试一下

让十进制 -1 进行无符号右移 0 位

-1 是负数，在内存中二进制存储是补码即 1111 .... 1111 1111，32 位都是 1，我们在程序中写入 -1 >>> 0 运行得到十进制数字 4294967295 ，再使用二进制转换工具转为二进制得到的就是 32 位二进制 1111 .... 1111 1111，所以就算无符号右移 0 位，得出的依然是一个很大的正数

使用无符号右移 >>> 取整（正数）

无符号右移和有符号右移以及左移都差不多，移 0 位都可取整，只不过无符号右移只能支持正数的取整，至于原理，说过无数遍了，相信你已经记住了，如下

1.323 >>> 0; // 1
2.324 >>> 0; // 2

位图法

可以解决海量数据的存在性问题，又不占用很多内存的前提下。

位图法的原理主要就是利用 int 类型数据，一个 int 类型数据是 4 个字节，一个字节 8 位，然后一个 int 数据利用自身字节位就可以表示 0-31 的数是否存在，bit 位表示数值，位山 0，1 值表示这个数值是否存在。

所有的 int 类型数据一共有2^32/8 = 2^29 Byte 约等于 512MB（2^10=1KB 2^20 =1MB 2^30=1GB）表示所有的 int 类型数需要 512MB，现在的计算机完全可以胜任，这些可以表示多少位数呢就是一个 int 可以表示 32 个数，32*2^32=2^37 约等于 10^11 百亿级别；

具体方案

那么接下来我们只需要申请一个 int 数组长度为 int tmp[N/32+1]即可存储完这些数据，其中 N 代表要进行查找的总数（这里也就是 2^32），tmp 中的每个元素在内存在占 32 位可以对应表示十进制数 0~31,所以可得到 BitMap 表:

tmp[0]:可表示 0~31

tmp[1]:可表示 32~63

tmp[2]可表示 64~95

~~

假设这 10 亿 int 数据为：6,3,8,32,36,……，那么具体的 BitMap 表示为：

使用如何快速查找具体的是否存在：

(1). 如何判断 int 数字放在哪一个 tmp 数组中：将数字直接除以 32 取整数部分(x/32)，例如：整数 8 除以 32 取整等于 0，那么 8 就在 tmp[0]上；

(2). 如何确定数字放在 32 个位中的哪个位：将数字 mod32 取模(x%32)。上例中我们如何确定 8 在 tmp[0]中的 32 个位中的哪个位，这种情况直接 mod 上 32 就 ok，又如整数 8，在 tmp[0]中的第 8 mod 上 32 等于 8，那么整数 8 就在 tmp[0]中的第八个 bit 位（从右边数起）。

对于多次出现的数据处理方法

然后我们怎么统计只出现一次的数呢？每一个数出现的情况我们可以分为三种：0 次、1 次、大于 1 次。也就是说我们需要用 2 个 bit 位才能表示每个数的出现情况。此时则三种情况分别对应的 bit 位表示是：00、01、11

我们顺序扫描这 10 亿的数，在对应的双 bit 位上标记该数出现的次数。最后取出所有双 bit 位为 01 的 int 型数就可以了。

哈希表原理

HashMap 原理技术知识整理

保存数据有两种比较简单的数据结构：数组 和 链表。

• 数组：寻址容易，插入和删除困难；
• 链表：寻址困难，但插入和删除容易。

把数组和链表这两种结构结合在一起，发挥出各自的优势，这种结构就是哈希表。

哈希表的底层实际上是基于数组来存储的，当插入键值对时，并不是直接插入该数组中，而是通过对键进行 Hash 运算得到 Hash 值，然后和数组容量取模，得到在数组中的位置后再插入。取值时，先对指定的键求 Hash 值，再和容量取模得到底层数组中对应的位置，如果指定的键值与存贮的键相匹配，则返回该键值对，如果不匹配，则表示哈希表中没有对应的键值对。这样做的好处是在查找、插入、删除等操作可以做到，最坏的情况是，当然这种是最极端的情况，极少遇到。

数组：采用一段连续的存储单元来存储数据。对于指定下标的查找，时间复杂度为 O(1)；通过给定值进行查找，需要遍历数组，逐一比对给定关键字和数组元素，时间复杂度为 O(n)，当然，对于有序数组，则可采用二分查找，插值查找，斐波那契查找等方式，可将查找复杂度提高为 O(logn)；对于一般的插入删除操作，涉及到数组元素的移动，其平均复杂度也为 O(n)

线性链表：对于链表的新增，删除等操作（在找到指定操作位置后），仅需处理结点间的引用即可，时间复杂度为 O(1)，而查找操作需要遍历链表逐一进行比对，复杂度为 O(n)

二叉树：对一棵相对平衡的有序二叉树，对其进行插入，查找，删除等操作，平均复杂度均为 O(logn)。

哈希表：相比上述几种数据结构，在哈希表中进行添加，删除，查找等操作，性能十分之高，不考虑哈希冲突的情况下，仅需一次定位即可完成，时间复杂度为 O(1)，接下来我们就来看看哈希表是如何实现达到惊艳的常数阶 O(1)的。

数据结构的物理存储结构只有两种：顺序存储结构和链式存储结构（像栈，队列，树，图等是从逻辑结构去抽象的，映射到内存中，也这两种物理组织形式），而在上面我们提到过，在数组中根据下标查找某个元素，一次定位就可以达到，哈希表利用了这种特性，哈希表的主干就是数组。

比如我们要新增或查找某个元素，我们通过把当前元素的关键字 通过某个函数映射到数组中的某个位置，通过数组下标一次定位就可完成操作。

存储位置 = f(关键字)

其中，这个函数 f 一般称为哈希函数，这个函数的设计好坏会直接影响到哈希表的优劣。举个例子，比如我们要在哈希表中执行插入操作：

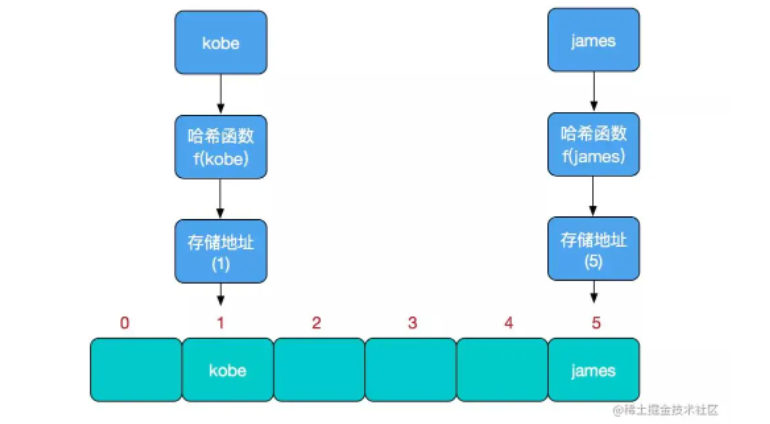
查找操作同理，先通过哈希函数计算出实际存储地址，然后从数组中对应地址取出即可

HashMap 底层就是一个数组结构，数组中的每一项又是一个链表

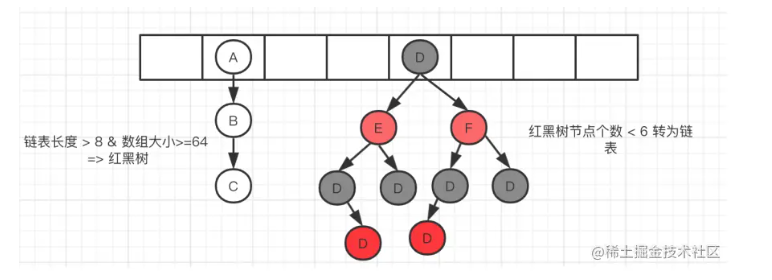
不管哪门语言，实现一个 HashMap 的过程均可分为三大步骤：

• 实现一个 Hash 函数
• 合理解决 Hash 冲突
• 实现 HashMap 的操作方法

简单来说，HashMap 由数组+链表组成的，数组是 HashMap 的主体，链表则是主要为了解决哈希冲突而存在的，如果定位到的数组位置不含链表（当前 entry 的 next 指向 null）,那么对于查找，添加等操作很快，仅需一次寻址即可；如果定位到的数组包含链表，对于添加操作，其时间复杂度为 O(n)，首先遍历链表，存在即覆盖，否则新增；对于查找操作来讲，仍需遍历链表，然后通过 key 对象的 equals 方法逐一比对查找。所以，性能考虑，HashMap 中的链表出现越少，性能才会越好

Hash 函数

Hash 函数非常重要，一个好的 Hash 函数不仅性能优越，而且还会让存储于底层数组中的值分配的更加均匀，减少冲突发生。之所以是减少冲突，是因为取 Hash 的过程，实际上是将输入键（定义域）映射到一个非常小的空间中，所以冲突是无法避免的，能做的只是减少 Hash 碰撞发生的概率。具体实现时，哈希函数算法可能不同，在 Rust 及很多语言的实现中，默认选择 SipHash 哈希算法。

默认情况下，Rust 的 HashMap 使用 SipHash 哈希算法，其旨在防止哈希表碰撞攻击，同时在各种工作负载上提供合理的性能。虽然 SipHash 在许多情况下表现出竞争优势，但其中一个比其它哈希算法要慢的情况是使用短键，例如整数。这就是为什么 Rust 程序员经常观察到 HashMap 表现不佳的原因。在这些情况下，经常推荐 FNV 哈希，但请注意，它不具备与 SipHash 相同的防碰撞性。

影响 Hash 碰撞（冲突）发生的除了 Hash 函数本身意外，底层数组容量也是一个重要原因。很明显，极端情况下如果数组容量为 1，哪必然发生碰撞，如果数组容量无限大，哪碰撞的概率非常之低。所以，哈希碰撞还取决于负载因子。负载因子是存储的键值对数目与数组容量的比值，比如数组容量 100，当前存贮了 90 个键值对，负载因子为 0.9。负载因子决定了哈希表什么时候扩容，如果负载因子的值太大，说明存储的键值对接近容量，增加碰撞的风险，如果值太小，则浪费空间。

所以，既然冲突无法避免，就必须要有解决 Hash 冲突的机制方法。

处理冲突的几种方法

主要有四类处理冲突的方法：

• 外部拉链法（常用）
• 开放定址法（常用）
• 公共溢出区（不常用）
• 再 Hash 法（不常用）

外部拉链法

主要思想是基于数组和链表的组合来解决冲突，桶（Bucket）中不直接存储键值对，每个 Bucket 都链接一个链表，当发生冲突时，将冲突的键值对插入链表中。外部拉链法的有点在于方法简单，非同义词之间也不会产生聚集现象（相比于开放定址法），并且其空间结构是动态申请的，所以比较适合无法确定表长的情况：缺点是链表指针需要额外的空间，遇到碰撞拒绝服务时会退化为单链表。

同义词：两个元素通过 Hash 函数得到了相同的索引地址，这两个元素就叫做同义词。

下面是外部拉链法的两种实现方法，主要区别在于桶（Bucket）中是否存储数据。

开放定址法

下图为线性探测:

公共溢出区

主要思想是建立一个独立的公共区，把冲突的键值对都放在其中。不常用，这里不再细述。

再 Hash 法

主要思想是有冲突时，换另外一个 Hash 函数来算 Hash 值。不常用，这里不再细述。

实现哈希表的操作方法

主要是：

• insert
• remove
• get
• contains_key
• ......等等......

其中最重要的是插入、查找、删除这三个操作

哈希函数

hash表（散列表）一般被用来加密，压缩等。 当选择的 hash 函数足够复杂时（难以破解），那么密码的明码通过此 hash 函数生成散列值的过程就是不可逆的，这往往被 IT 公司用来保存用户的密码，防止泄露。 hash table 被用来压缩，主要是因为通过 hash 函数映射后，数据存储的空间大大缩小，提高空间利用率，往往被用来处理大数据，这是由于通过hash 函数映射的散列值所占用的空间远远小于原数据。 以百度 TopK 面试题为例进行说明：

问题描述

搜索引擎会通过日志文件把用户每次检索使用的所有检索串都记录下来，每个查询串的长度为 1-255 字节。 假设目前有一千万个记录（这些查询串的重复度比较高，虽然总数是 1 千万，但如果除去重复后，不超过 3 百万个。一个查询串的重复度越高，说明查询它的用户越多，也就是越热门。），请你统计最热门的 10 个查询串，要求使用的内存不能超过 1G。

分析：

第一步：统计各个查询串出现的次数 1.首先直接将数据存入内存中是不合适的，因为根据题意此一千万条数据占用的内存大于 1G，所以不能选择内部排序。考虑外排后，再遍历所有数据统计频数。 2.外排时，文件排序用归并排序是最合适的，时间复杂度为 O(nlogn)。而用 hash table 的时间复杂度为 O（n）。

用法如下：

1.以查询串为 Key 值，以出现的次数为 value 创建哈希表，key 值通过哈希函数映射为数字，数字对数组长度取余，余数就为 hash 表的下表，将对应的数据进行存储。hash 表的实现方式有多种，邻接表是一个不错的实现。例如： 2.依次遍历数据，如果查询串已经在哈希表中存在，那么将次数加 1，如果不存在，通过映射进行存储，初始数据设为 1。这样一次遍历完后就将每个查询串的频数统计完毕。即使 300 万条记录均只出现一次且散列值不同，占用的存储空间也满足要求。 第二步：找出 Top10 这一步就是单纯的将查询串根据出现的频次进行排序。使用时间复杂度较小的堆排序，建立小顶堆（堆排序参考我的相关博文）。先遍历最初的十个数据建立小顶堆，然后依次遍历后续数据，和小顶堆根节点（最小的数据比较）。如果数据小于根节点，继续遍历。如果数据大于根节点，将根节点删除吗，将此数据放入堆中，调整为小顶堆，继续遍历比较。直到最后生成堆的是个数据便是 Top10。遍历的时间复杂度为 O(n),建堆调整堆的时间复杂度为 O((n-k)logk),此处 k 为 10。所以用堆操作的查找 Top10 时间复杂度为 O(nlogn)。 必须指出的是，hash table 的优劣完全依赖哈希函数的选取，一般选取哈希函数有取模取余，平方等。显然这些简单的哈希函数映射后会有冲突发生，多个 key 值对应同一个存储空间，当然邻接链表结构是可以很好解决。但选取一个合适的函数是非常必要的，一般的公式为 index=(valuex)>>28,右移，为除以 2^28 次方。 推荐 x 选取使用斐波那契（Fibonacci）散列法 斐波那契序列：0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610， 987, 1597, 2584, 4181, 6765, 10946，… 对我们常见的 32 位整数而言，公式： index = (value 2654435769) >> 28 对于 64 位整数而言，这个乘数是 11400714819323198485

海量数据问题

海量数据处理

top K 问题

先拿 10000 个数建堆，然后一次添加剩余元素，如果大于堆顶的数（10000 中最小的），将这个数替换堆顶，并调整结构使之仍然是一个最小堆，这样，遍历完后，堆中的 10000 个数就是所需的最大的 10000 个。建堆时间复杂度是 O（mlogm），算法的时间复杂度为 O（nmlogm）（n 为 10 亿，m 为 10000）。

优化的方法：可以把所有 10 亿个数据分组存放，比如分别放在 1000 个文件中。这样处理就可以分别在每个文件的 10^6 个数据中找出最大的 10000 个数，合并到一起在再找出最终的结果。

在大规模数据处理中，经常会遇到的一类问题：在海量数据中找出出现频率最好的前 k 个数，或者从海量数据中找出最大的前 k 个数，这类问题通常被称为 top K 问题。例如，在搜索引擎中，统计搜索最热门的 10 个查询词；在歌曲库中统计下载最高的前 10 首歌等。 针对 top K 类问题，通常比较好的方案是分治+Trie 树/hash+小顶堆（就是上面提到的最小堆），即先将数据集按照 Hash 方法分解成多个小数据集，然后使用 Trie 树活着 Hash 统计每个小数据集中的 query 词频，之后用小顶堆求出每个数据集中出现频率最高的前 K 个数，最后在所有 top K 中求出最终的 top K。

有 1 亿个浮点数，如果找出期中最大的 10000 个？

最容易想到的方法是将数据全部排序，然后在排序后的集合中进行查找，最快的排序算法的时间复杂度一般为 O（nlogn），如快速排序。但是在 32 位的机器上，每个 float 类型占 4 个字节，1 亿个浮点数就要占用 400MB 的存储空间，对于一些可用内存小于 400M 的计算机而言，很显然是不能一次将全部数据读入内存进行排序的。其实即使内存能够满足要求（我机器内存都是 8GB），该方法也并不高效，因为题目的目的是寻找出最大的 10000 个数即可，而排序却是将所有的元素都排序了，做了很多的无用功。

第二种方法为局部淘汰法，该方法与排序方法类似，用一个容器保存前 10000 个数，然后将剩余的所有数字——与容器内的最小数字相比，如果所有后续的元素都比容器内的 10000 个数还小，那么容器内这个 10000 个数就是最大 10000 个数。如果某一后续元素比容器内最小数字大，则删掉容器内最小元素，并将该元素插入容器，最后遍历完这 1 亿个数，得到的结果容器中保存的数即为最终结果了。此时的时间复杂度为 O（n+m^2），其中 m 为容器的大小，即 10000。

第三种方法是分治法，将 1 亿个数据分成 100 份，每份 100 万个数据，找到每份数据中最大的 10000 个，最后在剩下的 10010000 个数据里面找出最大的 10000 个。如果 100 万数据选择足够理想，那么可以过滤掉 1 亿数据里面 99%的数据。100 万个数据里面查找最大的 10000 个数据的方法如下：用快速排序的方法，将数据分为 2 堆，如果大的那堆个数 N 大于 10000 个，继续对大堆快速排序一次分成 2 堆，如果大的那堆个数 N 大于 10000 个，继续对大堆快速排序一次分成 2 堆，如果大堆个数 N 小于 10000 个，就在小的那堆里面快速排序一次，找第 10000-n 大的数字；递归以上过程，就可以找到第 1w 大的数。参考上面的找出第 1w 大数字，就可以类似的方法找到前 10000 大数字了。此种方法需要每次的内存空间为 10^64=4MB，一共需要 101 次这样的比较。

第四种方法是Hash 法。如果这 1 亿个书里面有很多重复的数，先通过 Hash 法，把这 1 亿个数字去重复，这样如果重复率很高的话，会减少很大的内存用量，从而缩小运算空间，然后通过分治法或最小堆法查找最大的 10000 个数。

第五种方法采用最小堆。首先读入前 10000 个数来创建大小为 10000 的最小堆，建堆的时间复杂度为 O（mlogm）（m 为数组的大小即为 10000），然后遍历后续的数字，并于堆顶（最小）数字进行比较。如果比最小的数小，则继续读取后续数字；如果比堆顶数字大，则替换堆顶元素并重新调整堆为最小堆。整个过程直至 1 亿个数全部遍历完为止。然后按照中序遍历的方式输出当前堆中的所有 10000 个数字。该算法的时间复杂度为 O（nmlogm），空间复杂度是 10000（常数）。

实际运行： 实际上，最优的解决方案应该是最符合实际设计需求的方案，在时间应用中，可能有足够大的内存，那么直接将数据扔到内存中一次性处理即可，也可能机器有多个核，这样可以采用多线程处理整个数据集。

下面针对不容的应用场景，分析了适合相应应用场景的解决方案。

（1）单机+单核+足够大内存 如果需要查找 10 亿个查询次（每个占 8B）中出现频率最高的 10 个，考虑到每个查询词占 8B，则 10 亿个查询次所需的内存大约是 10^9 * 8B=8GB 内存。如果有这么大内存，直接在内存中对查询次进行排序，顺序遍历找出 10 个出现频率最大的即可。这种方法简单快速，使用。然后，也可以先用 HashMap 求出每个词出现的频率，然后求出频率最大的 10 个词。

（2）单机+多核+足够大内存 这时可以直接在内存总使用 Hash 方法将数据划分成 n 个 partition，每个 partition 交给一个线程处理，线程的处理逻辑同（1）类似，最后一个线程将结果归并。

​ 该方法存在一个瓶颈会明显影响效率，即数据倾斜。每个线程的处理速度可能不同，快的线程需要等待慢的线程，最终的处理速度取决于慢的线程。而针对此问题，解决的方法是，将数据划分成 c×n 个 partition（c>1），每个线程处理完当前 partition 后主动取下一个 partition 继续处理，知道所有数据处理完毕，最后由一个线程进行归并。

（3）单机+单核+受限内存 这种情况下，需要将原数据文件切割成一个一个小文件，如次啊用 hash(x)%M，将原文件中的数据切割成 M 小文件，如果小文件仍大于内存大小，继续采用 Hash 的方法对数据文件进行分割，知道每个小文件小于内存大小，这样每个文件可放到内存中处理。采用（1）的方法依次处理每个小文件。

（4）多机+受限内存 这种情况，为了合理利用多台机器的资源，可将数据分发到多台机器上，每台机器采用（3）中的策略解决本地的数据。可采用 hash+socket 方法进行数据分发。

​ 从实际应用的角度考虑，（1）（2）（3）（4）方案并不可行，因为在大规模数据处理环境下，作业效率并不是首要考虑的问题，算法的扩展性和容错性才是首要考虑的。算法应该具有良好的扩展性，以便数据量进一步加大（随着业务的发展，数据量加大是必然的）时，在不修改算法框架的前提下，可达到近似的线性比；算法应该具有容错性，即当前某个文件处理失败后，能自动将其交给另外一个线程继续处理，而不是从头开始处理。

​ top K 问题很适合采用 MapReduce 框架解决，用户只需编写一个 Map 函数和两个 Reduce 函数，然后提交到 Hadoop（采用 Mapchain 和 Reducechain）上即可解决该问题。具体而言，就是首先根据数据值或者把数据 hash(MD5)后的值按照范围划分到不同的机器上，最好可以让数据划分后一次读入内存，这样不同的机器负责处理不同的数值范围，实际上就是 Map。得到结果后，各个机器只需拿出各自出现次数最多的前 N 个数据，然后汇总，选出所有的数据中出现次数最多的前 N 个数据，这实际上就是 Reduce 过程。对于 Map 函数，采用 Hash 算法，将 Hash 值相同的数据交给同一个 Reduce task；对于第一个 Reduce 函数，采用 HashMap 统计出每个词出现的频率，对于第二个 Reduce 函数，统计所有 Reduce task，输出数据中的 top K 即可。

​ 直接将数据均分到不同的机器上进行处理是无法得到正确的结果的。因为一个数据可能被均分到不同的机器上，而另一个则可能完全聚集到一个机器上，同时还可能存在具有相同数目的数据。

以下是一些经常被提及的该类问题。 （1）有 10000000 个记录，这些查询串的重复度比较高，如果除去重复后，不超过 3000000 个。一个查询串的重复度越高，说明查询它的用户越多，也就是越热门。请统计最热门的 10 个查询串，要求使用的内存不能超过 1GB。

（2）有 10 个文件，每个文件 1GB，每个文件的每一行存放的都是用户的 query，每个文件的 query 都可能重复。按照 query 的频度排序。

（3）有一个 1GB 大小的文件，里面的每一行是一个词，词的大小不超过 16 个字节，内存限制大小是 1MB。返回频数最高的 100 个词。

（4）提取某日访问网站次数最多的那个 IP。

（5）10 亿个整数找出重复次数最多的 100 个整数。

（6）搜索的输入信息是一个字符串，统计 300 万条输入信息中最热门的前 10 条，每次输入的一个字符串为不超过 255B，内存使用只有 1GB。

（7）有 1000 万个身份证号以及他们对应的数据，身份证号可能重复，找出出现次数最多的身份证号。

重复问题

在海量数据中查找出重复出现的元素或者去除重复出现的元素也是常考的问题。针对此类问题，一般可以通过位图法实现。例如，已知某个文件内包含一些电话号码，每个号码为 8 位数字，统计不同号码的个数。

​ 本题最好的解决方法是通过使用位图法来实现。8 位整数可以表示的最大十进制数值为 99999999。如果每个数字对应于位图中一个 bit 位，那么存储 8 位整数大约需要 99MB。因为 1B=8bit，所以 99Mbit 折合成内存为 99/8=12.375MB 的内存，即可以只用 12.375MB 的内存表示所有的 8 位数电话号码的内容。

输入输出练习

常用数据结构

一维数组

c++

int arr=[n]
vector<int> dp(n)

javascript

const arr = [];
const arr = Array(n);
const arr = new Array(n);
const arr = Array(n).fill(0);

二维数组

c++

vector<vector<int>> dp(n,vector<int>(m))
n*m可扩展二维数组   长度可以直接扩展

javascript

推荐使用

const dp=Array(m+1).fill().map(()=>Array(n+1).fill(0))

const dp=[] dp.push([])

const dp = new Array(n).fill([0,0])
const dp = Array.from(Array(n), () => Array(n).fill(0));
const dp = new Array(word1.length + 1).fill(0)
        .map(() => new Array(word2.length + 1).fill(0))

const dp = Array(m + 1).fill()  //fill()必需有
        .map(() =>Array(n + 1).fill(0))
const dp=[]  dp.push([])

哈希表（Map)

举个例子，假设要根据同学的名字查找对应的成绩，如果用 Array 实现，需要两个 Array：

var names = ["Michael", "Bob", "Tracy"];
var scores = [95, 75, 85];

给定一个名字，要查找对应的成绩，就先要在 names 中找到对应的位置，再从 scores 取出对应的成绩，Array 越长，耗时越长。

如果用 Map 实现，只需要一个“名字”-“成绩”的对照表，直接根据名字查找成绩，无论这个表有多大，查找速度都不会变慢。

用 JavaScript 写一个 Map 如下：

var m = new Map([
  ["Michael", 95],
  ["Bob", 75],
  ["Tracy", 85],
]);
m.get("Michael"); // 95

初始化 Map 需要一个二维数组，或者直接初始化一个空 Map。Map 具有以下方法：

var m = new Map(); // 空Map
m.set("Adam", 67); // 添加新的key-value
m.set("Bob", 59);
m.has("Adam"); // 是否存在key 'Adam': true
m.get("Adam"); // 67
m.delete("Adam"); // 删除key 'Adam'
m.get("Adam"); // undefined

• set(key, val): 向 Map 中添加新元素

• get(key): 通过键值查找特定的数值并返回

• has(key): 判断 Map 对象中是否有 Key 所对应的值，有返回 true，否则返回 false

• delete(key): 通过键值从 Map 中移除对应的数据

• clear(): 将这个 Map 中的所有元素删除

• keys()：返回键名的遍历器

• values()：返回键值的遍历器

• entries()：返回键值对的遍历器

• forEach()：使用回调函数遍历每个成员

常用

for(let i=0;i<arr.length;i++){
    map.set(arr[i],(map.get(arr[i]||0)+1)
}
const count=Array.from(map).sort((a,b)=>{
        return b[1]-a[1]
    })

集合(Set)

Set 和 Map 类似，也是一组 key 的集合，但不存储 value。由于 key 不能重复，所以，在 Set 中，没有重复的 key。

要创建一个 Set，需要提供一个 Array 作为输入，或者直接创建一个空 Set：

var s1 = new Set(); // 空Set
var s2 = new Set([1, 2, 3]); // 含1, 2, 3

重复元素在 Set 中自动被过滤：

var s = new Set([1, 2, 3, 3, "3"]);
s; // Set {1, 2, 3, "3"}

通过 add(key)方法可以添加元素到 Set 中，可以重复添加，但不会有效果：

s.add(4);
s; // Set {1, 2, 3, 4}
s.add(4);
s; // 仍然是 Set {1, 2, 3, 4}

通过 delete(key)方法可以删除元素：

var s = new Set([1, 2, 3]);
s; // Set {1, 2, 3}
s.delete(3);
s; // Set {1, 2}

• add(value)：添加某个值，返回 Set 结构本身(可以链式调用)。

• delete(value)：删除某个值，删除成功返回 true，否则返回 false。

• has(value)：返回一个布尔值，表示该值是否为 Set 的成员。

• clear()：清除所有成员，没有返回值。

• keys()：返回键名的遍历器。

• values()：返回键值的遍历器。

• entries()：返回键值对的遍历器。

• forEach()：使用回调函数遍历每个成员。

链表

function ListNode(val, next) {
  this.val = val === undefined ? 0 : val;
  this.next = next === undefined ? null : next;
}

二叉树

function TreeNode(val, left, right) {
  this.val = val === undefined ? 0 : val;
  this.left = left === undefined ? null : left;
  this.right = right === undefined ? null : right;
}

基本输入

牛客网 v8 模式是 readline()

赛码网 v8 模式是 read_line()

node 模式通用模板

let buf = "";
process.stdin.on("readable", function () {
  let chunk = process.stdin.read();
  if (chunk) buf += chunk.toString();
});
process.stdin.on("end", function () {
  buf.split("\n").forEach(function (line, lineIdx) {
    line = line.split(" ");
  });
});

单行输入

两数相加

js

注意问题 输入得到的字符串 需要进行去除空格转换成字符数组 然后再进行 parseInt

技巧 对于多个数组可以考虑 arr.map((item)=>item*1) 不必每个都 parseInt() (四则运算中只有加法会影响 字符串和数字的运算 str*1 会优先转换成数字)

v8 模式

var line;
while ((line = read_line())) {
  line = line.split(" ");
  print(parseInt(line[0]) + parseInt(line[1]));
}

node 模式

var readline = require("readline");
const reader = readline.createInterface({
  input: process.stdin,
  output: process.stdout,
});
reader.on("line", function (line) {
  var tokens = line.split(" ");
  console.log(parseInt(tokens[0]) + parseInt(tokens[1]));
});

可以直接 +tokens[0]转成数字 或者1*tokens[0]

console.log()本身就换行

换行 console.log(a+'\n')

简化

let n=parseInt(readline())

let arr=readline().split(' ').map(Number)

固定行输入

例如输入

3

1 2 3 4 5 6

表示

输入三个数组

v8 模式

var line = read_line();
line = line.split(" ");
var m = parseInt(line[0]);
var n = parseInt(line[1]);
console.log(m);
console.log(n);
var a = [],
  b = [];
while (m--) {
  var sum = read_line();
  sum = sum.split(" ");
  var x = parseInt(sum[0]);
  var y = parseInt(sum[1]);
  a.push(x);
  b.push(y);
}
console.log(a);
console.log(b);

node 模式 模板

let buf='';
process.stdin.on('readable', function () {
    let chunk = process.stdin.read();
    if (chunk) buf += chunk.toString();
});
let getInputNums = line => line.split(' ').filter(s => s !== '').map(x => parseInt(x));
let getInputStr = line => line.split(' ').filter(s => s !== '');
process.stdin.on('end', function () {
    buf.split('\n').forEach(function (line, lineIdx) {
         if (lineIdx === 0) {
            n = getInputNums(line)[0];
            m = getInputNums(line)[1];
        } else if (lineIdx <= n) {
            let a = getInputNums(line)[0];
            let b = getInputNums(line)[1];
            v[lineIdx] = a;
            w[lineIdx] = b;
          if(lineIdx===n) console.log(func(v,w,n,m))
    })
});
func(v,w,n,m)

输入二维数组

输入

3
1 2 3
4 5 6
7 8 9

var line = readline();
line = line.split(" ");
var n = parseInt(line[0]);
var q = parseInt(line[1]);
var dp = Array(n + 1)
  .fill()
  .map(() => Array(n + 1).fill(0));
for (let i = 0; i < n; i++) {
  var row = readline();
  row = row.split(" ");
  dp.push(row); //直接按行进行push
}

结构

• 接受输入
• 处理字符串数据
• 处理输入
• 传入参数，接受算法函数返回结果
• 编写算法函数

完全背包

输入

4 5
1 2
2 4
3 4
4 5

const N = 1010;

let v = new Int32Array(N);
let w = new Int32Array(N);
let f = [];
let init = (n) => {
  for (let i = 0; i <= n; i++) {
    f[i] = new Int32Array(N);
  }
};
let n = 0;
let buf = "";
process.stdin.on("readable", function () {
  let chunk = process.stdin.read();
  if (chunk) buf += chunk.toString();
});
let getInputNums = (line) =>
  line
    .split(" ")
    .filter((s) => s !== "")
    .map((x) => parseInt(x));
let getInputStr = (line) => line.split(" ").filter((s) => s !== "");
process.stdin.on("end", function () {
  buf.split("\n").forEach(function (line, lineIdx) {
    if (lineIdx === 0) {
      n = getInputNums(line)[0];
      m = getInputNums(line)[1];
      init(n);
    } else if (lineIdx <= n) {
      let a = getInputNums(line)[0];
      let b = getInputNums(line)[1];
      v[lineIdx] = a;
      w[lineIdx] = b;
      if (lineIdx === n) {
        for (let i = 1; i <= n; i++) {
          //件数
          for (let j = 0; j <= m; j++) {
            //体积
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = Math.max(f[i][j], f[i][j - v[i]] + w[i]);
          }
        }
        console.log(f[n][m]);
      }
    }
  });
});

合并区间

输入

5
1 2
2 4
5 6
7 8
7 9

let inputRanges = [];

let getRangeCount = (ranges) => {
  ranges.sort((a, b) => a[0] - b[0]);
  let result = 1;
  let curr = ranges[0];
  for (let i = 1; i < ranges.length; i++) {
    if (ranges[i][0] <= curr[1]) curr[1] = Math.max(curr[1], ranges[i][1]);
    else {
      result++;
      curr = ranges[i++];
    }
  }
  return result;
};
let buf = "";
process.stdin.on("readable", function () {
  let chunk = process.stdin.read();
  if (chunk) buf += chunk.toString();
});
let getInputArgs = (line) =>
  line
    .split(" ")
    .filter((s) => s !== "")
    .map((x) => parseInt(x));
process.stdin.on("end", function () {
  let n = 0;
  buf.split("\n").forEach(function (line, lineIdx) {
    if (lineIdx === 0) {
      let a = getInputArgs(line);
      n = a[0];
    } else if (lineIdx <= n) {
      inputRanges.push(getInputArgs(line));
      if (lineIdx === n) console.log(getRangeCount(inputRanges));
    }
  });
});

最长上升子序列

输入

7
3 1 2 1 8 5 6

const N = 1010;
let arr = [];
let f = new Int32Array(N).fill(1); //最长序列只有自己一个数
let a = new Int32Array(N);

let n = 0;

let buf = "";
process.stdin.on("readable", function () {
  let chunk = process.stdin.read();
  if (chunk) buf += chunk.toString();
});
let getInputNums = (line) =>
  line
    .split(" ")
    .filter((s) => s !== "")
    .map((x) => parseInt(x));
let getInputStr = (line) => line.split(" ").filter((s) => s !== "");
process.stdin.on("end", function () {
  buf.split("\n").forEach(function (line, lineIdx) {
    if (lineIdx === 0) {
      n = getInputNums(line)[0];
    } else if (lineIdx === 1) {
      arr = getInputStr(line);
      for (let i = 0; i < arr.length; i++) a[i + 1] = arr[i];
      for (let i = 1; i <= n; i++) {
        for (let j = 1; j < i; j++)
          if (a[j] < a[i]) f[i] = Math.max(f[i], f[j] + 1);
      }
      let res = 0;
      for (let i = 1; i <= n; i++) res = Math.max(res, f[i]);
      console.log(res);
    }
  });
});

不定行数输入字符串(无限输入)

输入多个字符串进行正则匹配

v8 模式

var line;
var reg = /^(?=.*[0-9])(?=.*[a-zA-Z])(?=.*[^a-zA-Z0-9]).{8,}$/;
while ((line = read_line())) {
  var ans = reg.test(line);
  if (ans) console.log("ok");
  else console.log("false");
}

node 模式

let buf = "";
process.stdin.on("readable", function () {
  let chunk = process.stdin.read();
  if (chunk) buf += chunk.toString();
});
process.stdin.on("end", function () {
  buf.split("\n").forEach(function (line, lineIdx) {
    if (line) {
      var ans = reg.test(line);
      if (ans) console.log("ok");
      else console.log("false");
    }
  });
});

c++模式

万能头文件

#include<bits/stdc++.h>

#include<iostream>
#include<regex>
using namespace std;
int main()
{   string str
    regex  reg("^(?=.*[0-9])(?=.*[a-zA-Z])(?=.*[^a-zA-Z0-9]).{8,}$");
    while(cin>>str){
    smatch result;
    bool ret = regex_match(str, result, reg);
    cout << (ret ? "合适" : "不合适") << endl;
    }
}

c++ stl 使用

算法竞赛 C++ STL 详解（容器、算法、迭代器）

STL 六大组件是什么?

STL 提供了六大组件，彼此之间可以组合套用，这六大组件分别是容器、算法、迭代器、仿函数、适配器、空间配置器。其中，在算法竞赛中用到最多的为容器、算法与迭代器。

• 容器(Container)：STL 容器为各种数据结构，如vector、stack、queue、map、set等，用来存放数据，从实现角度来看，STL 容器是一种class template。
• 算法(Algorithm)：STL 的算法多数定义在<algorithm>头文件中，其中包括了各种常用的算法，如sort、find、copy、reverse等，从实现角度来看，STL 算法是一种function template。
• 迭代器(Iterator)：STL 迭代器扮演了容器与算法之间的胶合剂，共有五种类型，从实现角度来看，迭代器是一种将opetator*、opetator->、operator++等指针相关操作予以重载的class template。所有 STL 容器都附带有自己专属的迭代器，只有容器的设计者才知道如何遍历自己的元素。
• 仿函数(Functor)：行为类似函数，可作为算法的某种策略，从实现角度来看，仿函数是一种重载了operator()的class或者class template。
• 适配器(Adaptor)：一种用来修饰容器或仿函数或迭代器接口的东西。
• 空间配置器(Allocator)：负责空间的配置与管理。从实现角度来看，配置器是一个实现了动态空间配置、空间管理、空间释放的class template。

STL 容器详解

① vector：又称变长数组，定义在<vector>头文件中，vector容器是动态空间，随着元素的加入，它的内部机制会自动扩充空间以容纳新的元素。因此vector的运用对于内存的合理利用与运用的灵活性有很大的帮助。

• vector的定义方式

vector<int> v;//定义一个vector，其中的元素为int类型
vector<int> v[N];//定义一个vector数组，其中有N个vector
vector<int> v(len);//定义一个长度为len的vector
vector<int> v(len, x);//定义一个长度为len的vector，初始化每个元素为x
vector<int> v2(v1);//用v1给v2赋值，v1的类型为vector
vector<int> v2(v1.begin(), v1.begin() + 3);//将v1中第0~2三个元素赋值给v2

• vector的常用内置函数

    //vector中的常用内置函数
vector<int> v = { 1, 2, 3 };//初始化vector，v:{1, 2, 3}
vector<int>::iterator it = v.begin();//定义vector的迭代器，指向begin()

v.push_back(4);//在vector的尾部插入元素4，v:{1, 2, 3, 4}
v.pop_back();//删除vector的最后一个元素，v:{1, 2, 3}
//注意使用lower_bound()与upper_bound()函数时vector必须是有序的，upper_bound()在<algorithm>中
lower_bound(v.begin(), v.end(), 2);//返回第一个大于等于2的元素的迭代器v.begin() + 1，若不存在则返回v.end()
upper_bound(v.begin(), v.end(), 2);//返回第一个大于2的元素的迭代器v.begin() + 2，若不存在则返回v.end()
v.size();//返回vector中元素的个数
v.empty();//返回vector是否为空，若为空则返回true否则返回false
v.front();//返回vector中的第一个元素
v.back();//返回vector中的最后一个元素
v.begin();//返回vector第一个元素的迭代器
v.end();//返回vector最后一个元素后一个位置的迭代器
v.clear();//清空vector
v.erase(v.begin());//删除迭代器it所指向的元素，即删除第一个元素
v.erase(v.begin(), v.begin() + 2);//删除区间[v.begin(), v.begin() + 2)的所有元素
v.insert(v.begin(), 1);//在迭代器it所指向的位置前插入元素1，返回插入元素的迭代器

//根据下标进行遍历
for (int i = 0; i < v.size(); i++)
cout << v[i] << ' ';
//使用迭代器遍历
for (vector<int>::iterator it = v.begin(); it != v.end(); it++)
cout << *it << ' ';
//for_each遍历(C++11)
for (auto x : v)
cout << x << ' ';

②stack：又称栈，是一种后进先出(Last In First Out，LIFO)的数据结构，定义在<stack>头文件中，stack容器允许新增元素、移除元素、取得栈顶元素，但是除了最顶端以外，没有任何方法可以存取stack的其它元素，换言之，stack不允许有遍历行为。

• stack的定义方式

    stack<int> stk;//定义一个stack，其中元素的类型为int
    stack<int> stk[N];//定义一个stack数组，其中有N个stack

• stack的常用内置函数

    //stack中的常用内置函数
    stack<int> stk;
stk.push(x);//在stack中插入元素x
stk.pop();//弹出stack的栈顶元素
stk.top();//返回stack的栈顶元素
stk.size();//返回stack中元素的个数
stk.empty();//返回stack是否为空，若为空则返回true否则返回false

③string：又称字符串，定义在<string>头文件中。C 风格的字符串(以空字符结尾的字符数组)太过复杂难于掌握，因此 C++标准库定义了一种string类。string和vector<char>在数据结构、内存管理等方面都是相同的。但是，vector<char>只是单纯的一个“ c h a r char char 元素的容器”，而string不仅是一个“ c h a r char char 元素的容器”，它还扩展了一些针对字符串的操作，例如string可以使用c_str()函数转换为 C 风格的字符串， vector中并未对输入输出流操作符进行重载，因此无法直接对vector<char>进行 c i n cin cin 或者 c o u t cout cout 这样的操作，但是string可以，vector<char>并不能直接实现字符串的拼接，但是string可以，string中重载了 + , + = +,+= +,+\=运算符。

• string的定义方式

string str;//定义一个空的字符串
string str[N];//定义一个string数组，其中有N个string
string str(5, 'a');//使用5个字符'a'初始化
string str("abc");//使用字符串初始化

• string的常用内置函数

    //string中的常用内置函数
    string str("abcabc");
str.push_back('d');//在string尾部插入字符，"abcabcd"
str.pop_back();//删除string尾部的字符，"abcabc"
str.length();//返回string中字符的个数
str.size();//作用与length()相同
str.empty();//返回string是否为空，若为空返回true否则返回false
str.substr(1);//返回string中从下标为1开始至末尾的子串，"bcabc"
str.substr(0, 2);//返回string中从下标为0开始长度为2的子串，"ab"
str.insert(1, 2, 'x');//在下标为1的字符前插入2个字符'x'，"axxbcabc"
str.insert(1, "yy");//在下标为1的字符前插入字符串"yy"，"ayyxxbcabc"
str.erase(1, 4);//删除从位置1开始的4个字符，"abcabc"
str.find('b');//返回字符'b'在string中第一次出现的位置，返回1，若不存在则返回-1
str.find('b', 2);//返回从位置2开始字符'b'在string中第一次出现的位置，返回4
str.find("bc");//同上，返回字符串第一次出现的位置，返回1，若不存在则返回-1
str.find("bc", 2);//返回4
str.rfind('b');//反向查找，原理同上，返回4，若不存在则返回-1
str.rfind('b', 3);//返回1
str.rfind("bc");//返回4，若不存在则返回-1
str.rfind("bc", 3);//返回1
stoi(str);//返回str的整数形式
to_string(value);//返回value的字符串形式，value为整型、浮点型等
str[0];//用下标访问string中的字符
cout << (str == str) << endl;//string可比较大小，按字典序

• string的erase()与remove()函数的用法

    //string中erase()与remove()的用法
string str1, str2, str3, str4, str5;
str1 = str2 = str3 = str4 = str5 = "I love AcWing! It's very funny!";
str1.erase(15);//删除[15,end())的所有元素，"I love AcWing!"
str2.erase(6, 11);//从第6个元素(包括)开始往后删除11个元素，"I love's very funny!"
str3.erase(str3.begin() + 2);//删除迭代器所指的元素，"I ove AcWing! It's very funny!"
str4.erase(str4.begin() + 7, str4.end() - 11);//删除[str4.begin()+7,str4.end()-11)的所有元素，"I love very funny!"
str5.erase(remove(str5.begin(), str5.end(), 'n'), str5.end());//删除[str5.begin(),str5.end())中所有字符'n'，"I love AcWig! It's very fuy!"

④queue：又称队列，是一种先进先出(First In First Out，FIFO)的数据结构，定义在<queue>头文件中，queue容器允许从一端(称为队尾)新增元素(入队)，从另一端(称为队头)移除元素(出队)。
⑤priority_queue：又称优先队列，同样定义在<queue>头文件中，与queue不同的地方在于我们可以自定义其中数据的优先级，优先级高的排在队列前面，优先出队。priority_queue具有queue的所有特性，包括基本操作，只是在这基础上添加了内部的一个排序，它的本质是用堆实现的，因此可分为小根堆与大根堆，小根堆中较小的元素排在前面，大根堆中较大的元素排在前面。注意：创建priority_queue时默认是大根堆！

• queue的定义方式

queue<int> que;//定义一个queue，其中元素的类型为int
queue<int> que[N];//定义一个queue数组，其中有N个queue
priority_queue<int> bigHeap;//定义一个大根堆
priority_queue<int, vector<int>, greater<int> > smallHeap;//定义一个小根堆

• queue的常用内置函数

    //queue中的常用内置函数
    queue<int> que;
    que.push(x);//在queue的队尾插入元素x
que.pop();//出队queue的队头元素
que.front();//返回queue的队头元素
que.back();//返回queue的队尾元素
que.size();//返回queue中元素的个数
que.empty();//返回queue是否为空，若为空则返回true否则返回false

⑥deque：又称双端队列，定义在<deque>头文件中，vector容器是单向开口的连续内存空间，deque则是一种双向开口的连续线性空间。所谓的双向开口，意思是可以在头尾两端分别做元素的插入和删除操作，当然，vector也可以在头尾两端插入元素，但是在其头部进行插入操作效率奇差，无法被接受。deque和vector最大的差异一是在于deque允许使用常数项时间在头部进行元素的插入和删除操作，二是在于deque没有容量的概念，因为它是动态的以分段连续空间组合而成，随时可以增加一段新的空间并链接起来。

• deque的定义方式

deque<int> deq;//定义一个deque，其中的元素为int类型
deque<int> deq[N];//定义一个deque数组，其中有N个deque
deque<int> deq(len);//定义一个长度为len的deque
deque<int> deq(len, x);//定义一个长度为len的deque，初始化每个元素为x
deque<int> deq2(deq1);//用deq1给v2赋值，deq2的类型为deque
deque<int> deq2(deq1.begin(), deq1.begin() + 3);//将deq1中第0~2三个元素赋值给deq2

• deque的常用内置函数

    //deque中的常用内置函数
    deque<int> deq = { 1, 2, 3 };//初始化vector，v:{1, 2, 3}
deque<int>::iterator it = deq.begin();//定义vector的迭代器，指向begin()

deq.push_back(4);//在deque的尾部插入元素4，v:{1, 2, 3, 4}
deq.pop_back();//删除deque的尾部元素，v:{1, 2, 3}
deq.push_front(4);//在deque的头部插入元素4，v:{4, 1, 2, 3}
deq.pop_front();//删除deque的头部元素，v:{1, 2, 3}
deq.size();//返回deque中元素的个数
deq.empty();//返回deque是否为空，若为空则返回true否则返回false
deq.front();//返回deque中的第一个元素
deq.back();//返回deque中的最后一个元素
deq.begin();//返回deque第一个元素的迭代器
deq.end();//返回deque最后一个元素后一个位置的迭代器
deq.clear();//清空deque
deq.erase(deq.begin());//删除迭代器it所指向的元素，即删除第一个元素
deq.erase(deq.begin(), deq.begin() + 2);//删除区间[v.begin(), v.begin() + 2)的所有元素
deq.insert(deq.begin(), 1);//在迭代器it所指向的位置前插入元素1，返回插入元素的迭代器

//根据下标进行遍历
for (int i = 0; i < deq.size(); i++)
cout << deq[i] << ' ';
//使用迭代器遍历
for (deque<int>::iterator it = deq.begin(); it != deq.end(); it++)
cout << *it << ' ';
//for_each遍历(C++11)
for (auto x : deq)
cout << x << ' ';

⑦map/multimap：又称映射，定义在<map>头文件中，map和multimap的底层实现机制都是红黑树。map的功能是能够将任意类型的元素映射到另一个任意类型的元素上，并且所有的元素都会根据元素的键值自动排序。map所有的元素都是pair，同时拥有实值和键值，pair的第一元素被视为键值，第二元素被视为实值，map不允许两个元素有相同的键值。multimap和map的操作类似，唯一区别是multimap的键值允许重复。

• map/multimap的定义方式

map<string, int> mp;//定义一个将string映射成int的map
map<string, int> mp[N];//定义一个map数组，其中有N个map
multimap<string, int> mulmp;//定义一个将string映射成int的multimap
multimap<string, int> mulmp[N];//定义一个multimap数组，其中有N个multimap

• map/multimap的常用内置函数

    //map/multimap中的常用内置函数
    map<string, int> mp;
mp["abc"] = 3;//将"abc"映射到3
mp["ab"]++;//将"ab"所映射的整数++
mp.insert(make_pair("cd", 2));//插入元素
mp.insert({ "ef", 5 });//同上
mp.size();//返回map中元素的个数
mp.empty();//返回map是否为空，若为空返回true否则返回false
mp.clear();//清空map
mp.erase("ef");//清除元素{"ef", 5}
mp["abc"];//返回"abc"映射的值
mp.begin();//返回map第一个元素的迭代器
mp.end();//返回map最后一个元素后一个位置的迭代器
mp.find("ab");//返回第一个键值为"ab"的迭代器，若不存在则返回mp.end()
mp.find({ "abc", 3 });//返回元素{"abc", 3}的迭代器，若不存在则返回mp.end()
mp.count("abc");//返回第一个键值为"abc"的元素数量1，由于map元素不能重复因此count返回值只有0或1
mp.count({ "abc", 2 });//返回第一个键值为"abc"的元素数量1，注意和find不一样，count只判断第一个键值
mp.lower_bound("abc");//返回第一个键值大于等于"abc"的元素的迭代器，{"abc", 3}
mp.upper_bound("abc");//返回第一个键值大于"abc"的元素的迭代器，{"cd", 2}

//使用迭代器遍历
for (map<string, int>::iterator it = mp.begin(); it != mp.end(); it++)
cout << (*it).first << ' ' << (*it).second << endl;
//for_each遍历(C++11)
for (auto x : mp)
cout << x.first << ' ' << x.second << endl;
//扩展推断范围的for_each遍历(C++17)
for (auto &[k, v] : mp)
cout << k << ' ' << v << endl;

⑧set/multiset：又称集合，定义在<set>头文件中。set的特性是所有元素都会根据元素的键值自动被排序，set的元素不像map那样可以同时拥有实值和键值，set的元素既是键值又是实值，set不允许两个元素有相同的键值，因此总结来说就是set中的元素是有序且不重复的。multiset的特性和用法和set完全相同，唯一的区别在于multiset允许有重复元素，set和multiset的底层实现都是红黑树。

• set/multiset的定义方式

set<int> st;//定义一个set，其中的元素类型为int
set<int> st[N];//定义一个set数组，其中有N个set
multiset<int> mulst;//定义一个multiset
multiset<int> mulst[N];//定义一个multiset数组，其中有N个multiset

• set/multiset的常用内置函数

    //set/multiset中的常用内置函数
set<int> st;
st.insert(5);//插入元素5
st.insert(6);//同上
st.insert(7);//同上
st.size();//返回set中元素的个数
st.empty();//返回set是否为空，若为空返回true否则返回false
st.erase(6);//清除元素6
st.begin();//返回set第一个元素的迭代器
st.end();//返回set最后一个元素后一个位置的迭代器
st.clear();//清空set
st.find(5);//返回元素5的迭代器，若不存在则返回st.end()
st.count(5);//返回元素5的个数1，由于set元素不会重复，因此count返回值只有0或1
st.lower_bound(5);//返回第一个键值大于等于5的元素的迭代器，返回元素5的迭代器
st.upper_bound(5);//返回第一个键值大于5的元素的迭代器，返回元素7的迭代器

//使用迭代器遍历
for (set<int>::iterator it = st.begin(); it != st.end(); it++)
cout << (*it) << ' ';
//for_each遍历(C++11)
for (auto x : st)
cout << x << ' ';

⑨unordered_map/unordered_set：分别定义在<unordered_map>与<unordered_set>头文件中，内部采用的是hash表结构，拥有快速检索的功能。与map/set相比最大的区别在于unordered_map/unordered_set中的元素是无序的，增删改查的时间复杂度为O(1)(map/set增删改查的时间复杂度为O(logn))，但是不支持lower_bound()/upper_bound()函数。

• unordered_map/unordered_set的定义方式

unordered_set<int> st;//定义一个unordered_set，其中的元素类型为int
unordered_set<int> st[N];//定义一个unordered_set数组，其中有N个unordered_set
unordered_map<int, int> mp;//定义一个unordered_map
unordered_map<int, int> mp[N];//定义一个unordered_map数组，其中有N个unordered_map

• unordered_map/unordered_set的常用内置函数

    //unordered_map/unordered_set中的常用内置函数
    unordered_set<int> st;
unordered_map<int, int> mp;
st.insert(5);//插入元素5
st.insert(6);//同上
st.insert(7);//同上
st.size();//返回unordered_set中元素的个数
st.empty();//返回unordered_set是否为空，若为空返回true否则返回false
st.erase(6);//清除元素6
st.begin();//返回unordered_set第一个元素的迭代器
st.end();//返回unordered_set最后一个元素后一个位置的迭代器
st.clear();//清空unordered_set
mp.insert(make_pair(1, 2));//插入元素{1, 2}
mp.insert({ 3, 4 });//同上
mp.size();//返回unordered_map中元素的个数
mp.empty();//返回unordered_map是否为空，若为空返回true否则返回false
mp.erase(3);//清除元素{3, 4}
mp.begin();//返回unordered_map第一个元素的迭代器
mp.end();//返回unordered_map最后一个元素后一个位置的迭代器
mp.clear();//清空unordered_map

//使用迭代器遍历
for (unordered_set<int>::iterator it = st.begin(); it != st.end(); it++)
cout << (*it) << ' ';
//for_each遍历(C++11)
for (auto x : st)
cout << x << ' ';

//使用迭代器遍历
for (unordered_map<int, int>::iterator it = mp.begin(); it != mp.end(); it++)
cout << (*it).first << ' ' << (*it).second << endl;
//for_each遍历(C++11)
for (auto x : mp)
cout << x.first << ' ' << x.second << endl;
//扩展推断范围的for_each遍历(C++17)
for (auto &[k, v] : mp)
cout << k << ' ' << v << endl;

STL 算法详解

C++标准库定义了一组泛型算法，之所以称为泛型指的是它们可以操作在多种容器上，不但可以作用于标准库类型，还可以用在内置数组类型甚至其它类型的序列上。泛型算法定义在<algorithm>头文件中，标准库还定义了一组泛化的算术算法(Generalized Numeric Algorithm)，定义在<numeric>头文件中。

#include <iostream>
#include <algorithm>
#include <numeric>
using namespace std;

int main()
{
//使用STL容器时将数组地址改为迭代器即可

int a[5] = { 1, 2, 3, 4, 5 };

//排序算法
sort(a, a + 5);//将区间[0, 5)内元素按字典序从小到大排序
sort(a, a + 5, greater<int>());//将区间[0, 5)内元素按字典序从大到小排序
reverse(a, a + 5);//将区间[0, 5)内元素翻转
nth_element(a, a + 3, a + 5);//将区间[0, 5)中第a + 3个数归位，即将第3大的元素放到正确的位置上，该元素前后的元素不一定有序

//查找与统计算法
find(a, a + 5, 3);//在区间[0, 5)内查找等于3的元素，返回迭代器，若不存在则返回end()
binary_search(a, a + 5, 2);//二分查找区间[0, 5)内是否存在元素2，若存在返回true否则返回false
count(a, a + 5, 3);//返回区间[0, 5)内元素3的个数

//可变序列算法
copy(a, a + 2, a + 3);//将区间[0, 2)的元素复制到以a+3开始的区间，即[3, 5)
replace(a, a + 5, 3, 4);//将区间[0, 5)内等于3的元素替换为4
fill(a, a + 5, 1);//将1写入区间[0, 5)中(初始化数组函数)
unique(a, a + 5);//将相邻元素间的重复元素全部移动至末端，返回去重之后数组最后一个元素之后的地址
remove(a, a + 5, 3);//将区间[0, 5)中的元素3移至末端，返回新数组最后一个元素之后的地址

//排列算法
next_permutation(a, a + 5);//产生下一个排列{ 1, 2, 3, 5, 4 }
prev_permutation(a, a + 5);//产生上一个排列{ 1, 2, 3, 4, 5 }

//前缀和算法
partial_sum(a, a + 5, a);//计算数组a在区间[0, 5)内的前缀和并将结果保存至数组a中

return 0;
}