跳到主要内容

算法题

数组​

88. 合并两个有序数组​

88. 合并两个有序数组

从后往前遍历 

var merge = function(nums1, m, nums2, n) {
        let i=m-1,j=n-1,k=m+n-1;
        while(i>=0||j>=0){
            if(i<0)nums1[k--]=nums2[j--];
            else if (j<0) nums1[k--]=nums1[i--];
            else if(nums1[i]<nums2[j]) nums1[k--]=nums2[j--];
            else nums1[k--]=nums1[i--];
        }
        return nums1;
};

54. 螺旋矩阵​

54. 螺旋矩阵

var spiralOrder = function (matrix) {
    if (matrix.length === 0) return []
    const res = []
    let top = 0, bottom = matrix.length - 1, left = 0, right = matrix[0].length - 1
    while (top < bottom && left < right) {
        for (let i = left; i < right; i++) res.push(matrix[top][i])   // 上层
        for (let i = top; i < bottom; i++) res.push(matrix[i][right]) // 右层
        for (let i = right; i > left; i--) res.push(matrix[bottom][i])// 下层
        for (let i = bottom; i > top; i--) res.push(matrix[i][left])  // 左层
        right--
        top++
        bottom--
        left++  // 四个边界同时收缩，进入内层
    }
    if (top === bottom) // 剩下一行，从左到右依次添加
        for (let i = left; i <= right; i++) res.push(matrix[top][i])
    else if (left === right) // 剩下一列，从上到下依次添加
        for (let i = top; i <= bottom; i++) res.push(matrix[i][left])
    return res
};

59. 螺旋矩阵 II​

59. 螺旋矩阵 II

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

输入：n = 3 输出：[[1,2,3],[8,9,4],[7,6,5]]

var generateMatrix = function(n) {
    let left = 0 //左
    let right = n - 1 //右
    let bottom = n - 1 //下
    let top = 0 //上
    const total = n * n //矩阵总数

    const dep = [] //初始化矩阵

    for(let i =0;i < n;i++) {
        dep[i] = []
    }

    let count = 0 //步数

    while(count < total) {
        for(let i = left;i <= right;i++) dep[left][i] = ++count // 从左往右
        top++
        for(let i = top;i <= bottom;i++) dep[i][right] = ++count // 从上往下
        right--
        for(let i = right;i >= left;i--) dep[bottom][i] = ++count // 从右往左
        bottom--
        for(let i = bottom;i >= top;i--) dep[i][left] = ++count // 从下往上
        left++
    }

    return dep
};

384. 打乱数组（洗牌算法）​

384. 打乱数组

class Solution {
    constructor(nums) {
        this.nums = nums;
        // 保存原始数组
        this.original = [...this.nums];
    }
    reset() {
        this.nums = [...this.original];
        return this.nums;
    }
    shuffle() { //洗牌算法
        const len = this.nums.length;
        for (let i = 0; i < len; i++) {
            // 获取区间[i,len-1]范围内的随机整数j
            const j = i + Math.floor(Math.random() * (this.nums.length - i));
            // 交换位置
            [this.nums[i], this.nums[j]] = [this.nums[j], this.nums[i]];
        }
        return this.nums;
    }
}

48. 旋转图像​

48. 旋转图像

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

var rotate = function (matrix) {
    const n = matrix.length;
    // 先水平翻转
    for (let i = 0; i < n / 2; i++) {
        for (let j = 0; j < n; j++) {
            [matrix[i][j], matrix[n - i - 1][j]] = [matrix[n - i - 1][j], matrix[i][j]]
        }
    }
    // 再对角线翻转
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < i; j++) {
            [matrix[i][j], matrix[j][i]] = [matrix[j][i], matrix[i][j]]
        }
    }
};

27. 移除元素​

27. 移除元素

//时间复杂度：O(n)
//空间复杂度：O(1)
var removeElement = (nums, val) => {
    let k = 0;
    for(let i = 0;i < nums.length;i++){
        if(nums[i] != val){
            nums[k++] = nums[i]
        }
    }
    return k;
};

498. 对角线遍历​

498. 对角线遍历

先上后下

var findDiagonalOrder = function (matrix) {
    if (matrix.length < 1) return [];
    let res = [],
        flag = true,  // true-右上 /  false-左下
        i = j = 0,
        n = matrix.length,
        m = matrix[0].length;

    while (i < n && j < m) {
        res.push(matrix[i][j]);
        m = matrix[i].length; // 每行的长度
        if (flag) {
            //  右上移动 i-=1; j+=1 
            i -= 1;
            j += 1;
        } else {
            // 左下移动 i+=1; j-=1
            i += 1;
            j -= 1;
        }
        // 处理边界 -- 转弯
        if (i < 0 || j < 0 || i == n || j == m) {
            if (flag) {
                // 右上
                if (j < m) i = 0; // 上边越界，像右移动
                else {
                    // 右边越界，向下移动
                    i += 2;
                    j--;
                }
            } else {
                // 左下
                if (i < n) j = 0; // 左边越界， 像下移动
                else {
                    // 下边越界， 想右移动
                    i--;
                    j += 2;
                }
            }
            flag = !flag; // 转换方向
        }
    }
    return res;
};

先下后上


var findDiagonalOrder = function (matrix) {
    if (matrix.length < 1) return [];
    let res = [],
        flag = true,  // true-右上 /  false-左下
        i = j = 0,
        n = matrix.length,
        m = matrix[0].length;

    while (i < n && j < m) {
        res.push(matrix[i][j]);
        m = matrix[i].length; // 每行的长度
        if (flag) {
            // 左下移动 i-=1; j+=1 
                i += 1;
            j -= 1;
        } else {
            // 右上移动 i+=1; j-=1
        i -= 1;
            j += 1;
        }
        // 处理边界 -- 转弯
        if (i < 0 || j < 0 || i == n || j == m) {
            if (flag) {
                // 右上
                if (i < m) j = 0; // 上边越界，像右移动
                else {
                    // 右边越界，向下移动
                    j += 2;
                    i--;
                }
            } else {
                // 左下
                if (j < n) i = 0; // 左边越界， 像下移动
                else {
                    // 下边越界， 想右移动
                    j--;
                    i += 2;
                }
            }
            flag = !flag; // 转换方向
        }
    }
    return res;
};
var mat = [[1, 2, 3], [4, 5, 6], [7, 8, 9]];
console.log(findDiagonalOrder(mat));

二维数组放大​

var arr = [
    [0,1],
    [1,0]
];

var newArr = [];
function bigArr(n,k,arr){
    for(let i = 0; i < n;i++){
        for(let j = 0; j < n; j++){
            let temp = arr[i][j];
            // console.log(temp);
            for(let ii = i*k; ii<i*k + k; ii++){
                //newArr[ii] = new Array(n*k);
                for(let jj = j*k; jj <j*k+k; jj++){
                    //newArr[ii] = new Array(n*k);
                    newArr[ii][jj]=temp;
                    // console.log(temp);
                    // console.log('ii:' + ii);
                    // console.log('jj:' + jj);
                    // console.log(newArr[ii][jj]);                   
                }
            }
        }
    }
    return newArr
}
var newA = bigArr(arr.length,3,arr)
console.log('原始数组：' );
console.log(arr);
console.log('放大倍数k:'+ 3);
console.log('放大后的数组:' );
console.log(newA);

双指针/滑动窗口​

3. 无重复字符的最长子串​

3. 无重复字符的最长子串

双指针移动 

var lengthOfLongestSubstring = function(s) {
 var cnt={};
    var res=0;
    var j=0;
for(let i=0;i<s.length;i++)
    {
        if(s[i] in cnt) cnt[s[i]]++;//存在重复 值加1
        else cnt[s[i]]=1;
        while (cnt[s[i]]>=2)
            {
                cnt[s[j]]--;//相当于删除窗口之外的元素
                j++; //右移
                //cnt[s[j++]]--;
            }
        res=Math.max(res,i-j+1);
    }
    return res;
};

15. 三数之和​

15. 三数之和

给你一个整数数组 nums ，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。请

你返回所有和为 0 且不重复的三元组。

注意：答案中不可以包含重复的三元组。

双指针

var threeSum = function(nums) {
        const len=nums.length;
        if(len<3) return [];
        nums.sort((a,b)=>a-b);
        const res=[];
        for(let i=0;i<len-2;i++){
            if(nums[i]>0) break;
            if(i>0&&nums[i]===nums[i-1]) continue;
            let left=i+1,right=len-1;
            while(left<right){
                const sum=nums[i]+nums[left]+nums[right];
                if(sum<0) {left++;continue }
                if(sum>0){right--;continue}
                res.push([nums[i],nums[left],nums[right]]);
                //去重
                while(left<right&&nums[left]===nums[left+1]) left++
                while(left<right&&nums[right]===nums[right-1])  right--
                left++
                right--
            }
            
        }
        return res;
};

通用解法

/**
 *  nsum通用解法，支持2sum，3sum，4sum...等等
 *  时间复杂度分析：
 *  1. n = 2时，时间复杂度O(NlogN)，排序所消耗的时间。、
 *  2. n > 2时，时间复杂度为O(N^n-1)，即N的n-1次方，至少是2次方，此时可省略排序所消耗的时间。举例：3sum为O(n^2)，4sum为O(n^3)
 * @param {number[]} nums
 * @return {number[][]}
 */
var threeSum = function (nums) {
    // nsum通用解法核心方法
    function nSumTarget(nums, n, start, target) {
        // 前提：nums要先排序好
        let res = [];
        if (n === 2) {
            res = towSumTarget(nums, start, target);
        } else {
            for (let i = start; i < nums.length; i++) {
                // 递归求(n - 1)sum
                let subRes = nSumTarget(
                    nums,
                    n - 1,
                    i + 1,
                    target - nums[i]
                );
                for (let j = 0; j < subRes.length; j++) {
                    res.push([nums[i], ...subRes[j]]);
                }
                // 跳过相同元素
                while (nums[i] === nums[i + 1]) i++;
            }
        }
        return res;
    }

    function towSumTarget(nums, start, target) {
        // 前提：nums要先排序好
        let res = [];
        let len = nums.length;
        let left = start;
        let right = len - 1;
        while (left < right) {
            let sum = nums[left] + nums[right];
            if (sum < target) {
                while (nums[left] === nums[left + 1]) left++;
                left++;
            } else if (sum > target) {
                while (nums[right] === nums[right - 1]) right--;
                right--;
            } else {
                // 相等
                res.push([nums[left], nums[right]]);
                // 跳过相同元素
                while (nums[left] === nums[left + 1]) left++;
                while (nums[right] === nums[right - 1]) right--;
                left++;
                right--;
            }
        }
        return res;
    }
    nums.sort((a, b) => a - b);
    // n = 3，此时求3sum之和
    return nSumTarget(nums, 3, 0, 0);
};

18. 四数之和​

18. 四数之和

返回满足下述全部条件且不重复的四元组 [nums[a], nums[b], nums[c], nums[d]] 

var fourSum = function(nums, target) {
    let len = nums.length;
    if(len < 4) return [];

    nums.sort((a, b) => a - b); // 排序
    
    let result = [];
    for(let i = 0; i < len - 3; i++) {
        if(i > 0 && nums[i] === nums[i - 1]) // 去重
            continue;

        for(let j = i + 1; j < len - 2; j++) {
            if(j > i + 1 && nums[j] === nums[j - 1]) // 去重
                continue;

            let left = j + 1; // 左指针初始化
            let right = len - 1; // 右指针初始化

            while(left < right) {
                if(nums[i] + nums[j] + nums[left] + nums[right] > target) {
                    right--; // 如果大于0，右指针左移，让和小一点
                } else if(nums[i] + nums[j] + nums[left] + nums[right] < target) {
                    left++; // 如果小于0，左指针右移，让和大一点
                } else {
                    result.push([nums[i], nums[j], nums[left], nums[right]]);
                    while(left < right && nums[right] === nums[right - 1]) {
                        right--; // 去重
                    }
                    while(left < right && nums[left] === nums[left + 1]) {
                        left++; // 去重
                    }
                    // 找到一个符合条件的四元组了，两指针同时收缩
                    right--;
                    left++;
                }
            }
        }
        
    }
    return result;
};

209.长度最小的子数组​

209. 长度最小的子数组

const minSubArrayLen = (s, nums) => {
  let minLen = Infinity;
  let i = 0;
  let j = 0;
  let sum = 0;
  while (j < nums.length) {   // 主旋律是扩张，找可行解
    sum += nums[j];
    while (sum >= s) {        // 间歇性收缩，优化可行解
      minLen = Math.min(minLen, j - i + 1);
      sum -= nums[i];
      i++;
    }
    j++;
  }
  return minLen === Infinity ? 0 : minLen; // 从未找到可行解，返回0
};

var minSubArrayLen = function(target, nums) {
    let slow = fast = sum = 0;
    let ans = Number.MAX_SAFE_INTEGER;
    for (; fast < nums.length; fast++) {
        sum += nums[fast];
        if (sum < target) {
            continue;
        }
        while (sum >= target) {
            ans = Math.min(ans, fast - slow + 1);
            sum -= nums[slow];
            slow++;
        }
    }
    return ans === Number.MAX_SAFE_INTEGER ? 0 : ans;
};

977.有序数组的平方​

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

输入：nums = [-4,-1,0,3,10] 输出：[0,1,9,16,100] 解释：平方后，数组变为 [16,1,0,9,100] 排序后，数组变为 [0,1,9,16,100]

两个指针，i指向头，j指向尾 两头开始遍历，比较平方数，然后从大到小，以此把数据放进新数组中 （可以采用保存上一次未移动的数的平方数，来减少以此求平方的计算）

var sortedSquares = function(A) {
    let [i, j] = [0, A.length - 1];
    let temp = [];
    while (i <= j) {
        const m = A[i] ** 2;
        const n = A[j] ** 2;
        if (m > n) {
            temp.unshift(m);
            ++i;
        } else {
            temp.unshift(n);
            --j;
        }
    }
    return temp;
};

42. 接雨水​

42. 接雨水

双指针法

var trap = function(height) {
    const len = height.length;
    let sum = 0;
    for(let i = 0; i < len; i++){
        // 第一个柱子和最后一个柱子不接雨水
        if(i == 0 || i == len - 1) continue;
        let rHeight = height[i]; // 记录右边柱子的最高高度
        let lHeight = height[i]; // 记录左边柱子的最高高度
        for(let r = i + 1; r < len; r++){
            if(height[r] > rHeight) rHeight = height[r];
        }
        for(let l = i - 1; l >= 0; l--){
            if(height[l] > lHeight) lHeight = height[l];
        }
        let h = Math.min(lHeight, rHeight) - height[i];
        if(h > 0) sum += h;
    }
    return sum;
};

动态规划法

var trap = function(height) {
    const len = height.length;
    if(len <= 2) return 0;
    const maxLeft = new Array(len).fill(0);
    const maxRight = new Array(len).fill(0);
    // 记录每个柱子左边柱子最大高度
    maxLeft[0] = height[0];
    for(let i = 1; i < len; i++){
        maxLeft[i] = Math.max(height[i], maxLeft[i - 1]);
    }
    // 记录每个柱子右边柱子最大高度
    maxRight[len - 1] = height[len - 1];
    for(let i = len - 2; i >= 0; i--){
        maxRight[i] = Math.max(height[i], maxRight[i + 1]);
    }
    // 求和
    let sum = 0;
    for(let i = 0; i < len; i++){
        let count = Math.min(maxLeft[i], maxRight[i]) - height[i];
        if(count > 0) sum += count;
    }
    return sum;
};

283. 移动零​

283. 移动零

var moveZeroes = function(nums) {
        if(nums==null){
            return
        }
        let j=0;
        for(let i=0;i<nums.length;i++){
            if(nums[i]!==0){
                let temp=nums[i];
                nums[i]=0;
                nums[j++]=temp;
            }
        }
};

字符串​

kmp算法​

什么是KMP算法​

说到KMP，先说一下KMP这个名字是怎么来的，为什么叫做KMP呢。

因为是由这三位学者发明的：Knuth，Morris和Pratt，所以取了三位学者名字的首字母。所以叫做KMP

KMP有什么用​

假设现在有一个文本字符串 aabaabaaf 和一个模板字符串 aabaaf，现在要求在文本串中找出模板串出现的第一个位置 (从0开始)。如果不存在，则返回 -1。

相信很多同学一开始可能都想到双重for循环的暴力解法，遍历文本串从下标 0 到下标 5 时，发现下标5指向的 b 与模板串中下标5指向的 f 不匹配，故又从文本串的下标 1 重新开始下一轮匹配，此时显然时间复杂度是O(mn)，m、n*分别是文本串与模板串的字符串长度。

例子中不难看出，最终答案应该是当我们遍历文本串第四轮，即从下标 3 开始匹配的字符串与模板串相同，但是这样就除了初始从 *0* 匹配 和最终从 *3* 匹配外，多了两次从1匹配和从2匹配的多余步骤，那么该怎么通过我们初始从 *0* 匹配中得到的数据（可以理解为“失败的经验”）中智能的跳过必定失败的遍历步骤呢？

此时我们发现，文本串中 0~2 位的aab是和3~5 位一样的，都能与模板串前几位匹配上，也就是说我们第一次匹配失败后，第二次完全可以从文本串下标为 3 的地方开始第二轮遍历，这就可以帮助我们省略掉了文本串中从下标1和下标2开始访问的，这就是KMP算法的主要思想当出现字符串不匹配时，可以知道一部分之前已经匹配的文本内容，可以利用这些信息避免从头再去做匹配了。

好了，理解完KMP算法的核心思想，我们接下来就来研究它如何如何记录已经匹配的文本内容 和 通过记录跳过多余匹配步骤，首先，让我们引入两个重要的知识点：前缀表和next数组

前缀表​

前缀、后缀、最长公共前后缀​

前缀是指不包含最后一个字符的所有以第一个字符开头的连续子串 后缀是指不包含第一个字符的所有以最后一个字符结尾的连续子串 例如我们上述模板串aabaaf中，前缀就包括：a,aa,aab,aaba.aabaa；后缀有：f,af,aaf,baaf,abaaf

那么，我们可以引出我们的最长公共前后缀(也叫做最长相等前后缀)：即一个字符串的 前缀集 和 后缀集 中最长的相等字串。上文中模板串aabaaf的前后缀集可以看出没有相等字串，所以它的最长相等前后缀为0

如： 字符串a的最长相等前后缀为0(注意字符串的前后缀定义，故单字符没有前后缀）；字符串aa的最长相等前后缀为1；字符串aaa的最长相等前后缀为2；等.....。

前缀表​

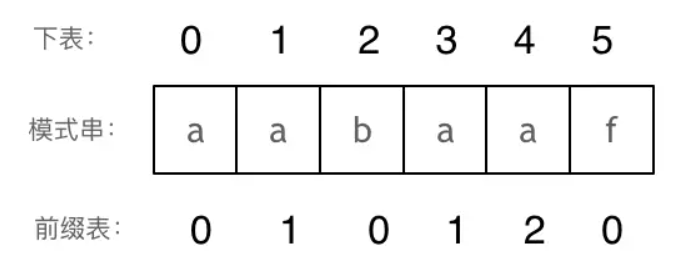
前缀表：记录下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。 前缀表的任务是当前位置匹配失败，找到之前已经匹配上的位置，再重新匹配，此也意味着在某个字符失配时，前缀表会告诉你下一步匹配中，模式串应该跳到哪个位置。 这就涉及到计算完整的前缀表:

image-20221004085142495解释一下：

  • 长度为前1个字符的子串a最长相同前后缀的长度为0；
  • 长度为前2个字符的子串aa最长相同前后缀的长度为1；
  • 长度为前3个字符的子串aab最长相同前后缀的长度为0；
  • 长度为前4个字符的子串aaba最长相同前后缀的长度为1；
  • 长度为前5个字符的子串aabaa最长相同前后缀的长度为2；
  • 长度为前6个字符的子串aabaaf最长相同前后缀的长度为0。

截至到目前，我们把前缀表算了出来。可以看出模板串与前缀表对应位置的数字表示的就是：下标i之前（包括i）的字符串中，有多大长度的相同前缀后缀。

前缀表怎么用 / 为什么一定要用前缀表​

前缀表为啥就能告诉我们 上次匹配的位置，并跳过去呢？ 回顾一下，刚刚匹配的过程在下标5的地方遇到不匹配，模式串是指向f，如图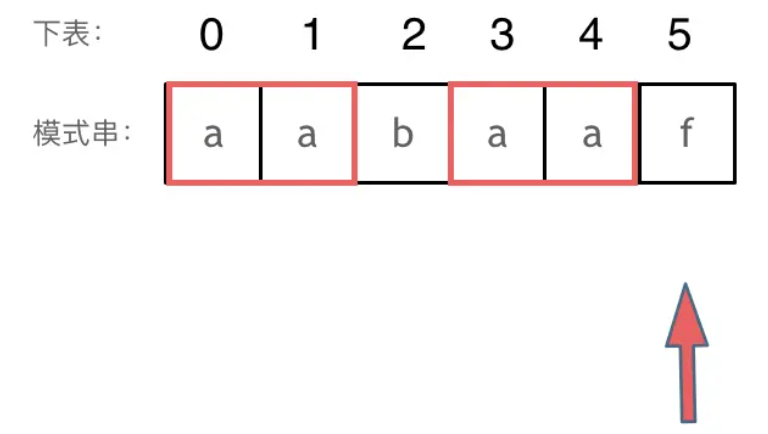： image-20221004085153704找到的不匹配的位置，那么此时我们要看它的前一个字符的前缀表的数值是多少。为什么要前一个字符的前缀表的数值呢，

下标5之前这部分的字符串（也就是字符串aabaa）的最长相等的前缀和后缀字符串是 子字符串aa ，我们可以通过对称思想，我可以拿模板串当前失败的后缀作为下一轮匹配的前缀（这样就省去了匹配公共前后缀片段的必失败轮次）。因为找到了最长相等的前缀和后缀，匹配失败的位置是后缀子串的后面，那么我们找到与其相同的前缀的后面从新匹配就可以了。

前一个字符的前缀表的数值是2， 所有把下标移动到下标2的位置继续比配（为什么移到2，因为相同前后缀的原因，后缀段aa肯定在文本串中已经匹配过了，那么我们可以替换为文本串已经匹配过前缀段aa了，也就是说文本串已经匹配成功前缀表数字代表的数量的字符了，即匹配完两个了从下标2第三个匹配起）。然后就找到了下标2，指向b，继续匹配：如图：image.png所以前缀表具有告诉我们当前位置匹配失败，跳到之前已经匹配过的地方的能力。

next数组​

什么是next数组​

next数组可以理解为就是把抽象的前缀表实例化，我们在做题中同样也是构造next数组来运用前缀表这种方法，而不同的使用next数组的方法因人而异，但原理是一样的只是在最终比较的时候有所出入，我们拿模板串 aabaaf举例：

  • 前缀表【0 1 0 1 2 0】作为next数组，比较到f跟文本串有出入，回退到上一位的前缀表对应的 2 作为下一次匹配的起始下标处
  • 前缀表【-1 0 1 0 1 2】作为next数组，就是将第一种的前缀表整体右移，初始值赋予 -1（或者存储字符串长度），比较到f跟文本串有出入，直接拿f的前缀表对应的数值作为下一次匹配的起始下标处、
  • 前缀表【-1 0 -1 0 1 -1】作为next数组，就是将第一种的前缀表整体-1，比较到f跟文本串有出入，回退到上一位的前缀表对应的值+1作为下一次匹配的起始下标处

那么使用next数组的时间复杂度分析：其中n为文本串长度，m为模式串长度，因为在匹配的过程中，根据前缀表不断调整匹配的位置，可以看出匹配的过程是O(n)，之前还要单独生成next数组，时间复杂度是O(m)。所以整个KMP算法的时间复杂度是O(n+m)的。

暴力的解法显而易见是O(n × m)，所以KMP在字符串匹配中极大的提高的搜索的效率。

构造next数组（难点）​

构造next数组就是对于题中给到的模板串，我们封装一个函数可以算出模板串的前缀表并返回的过程，算出前缀表的过程核心思想就是：接收模板串作为参数；i指针指向后缀末尾，j指针指向前缀末尾（注意：j还代表i位置之前子串的最长相等前后缀长度），i每次向后移动1位，求出以i指向字符为结尾的子串的最大相同前后缀，作为前缀表此位置next[i]的值

// 计算前缀表采用第一种方法（不右移也不减一）
const getNext = function(needle){
    let j = 0;   //j初始值从0，第一位开始
    let next = [];
    next[0] = j;  //数组next[0]为0，首位(单位)字符肯定没有前后缀
    for(let i=1; i<needle.length; i++){   //注意i从1开始
        // 前后缀不相同
        while (j>0 && needle[i] !== needle[j]){   //j要保证大于0，回退过程中比较前缀尾j与后缀尾i是否相等
            j = next[j-1];  //j回退到上一位，j到字符串首位还不相等说明当前i作为终止位的字串没有最长相等前后缀，next[i]赋值0
        }
        // 前后缀相同
        if (needle[i] === needle[j]){
            j++; //相同，j此时指向的是前缀字符串（上一级），要同时向后移动j和i准备下一轮匹配（移动i在for循环里）
        }
        next[i] = j;// 将j（前缀的长度）赋给next[i]
    }
    return next;
}

对于难点:为什么j同时表示最长相等前后缀？

j是前缀的末尾，也代表着前缀的长度，如果j不断地移进，说明i作为后缀的末尾正在遍历的部分与j作为前缀的末尾正在遍历的部分相同，相同的部分就是“相等前后缀”，那么j代表的数值就是“内容为从0位置开始到i的位置的字符串”的最大相等前后缀长度。

对于难点:为什么"前后缀不匹配时"，要用while循环持续回退？

首先要知道next数组对应的是前缀表，前缀表也称部分匹配表。该数组中的值代表着该子串中的最长相等前后缀，也是子串中已经匹配好的长度。如next【4】=2，其对应的子串是aabaa，前缀aa和后缀aa已经匹配好了，长度为2，j指针此时也停留在2。 每次求next[i]，可看作前缀与后缀的一次匹配，在该过程中就可以用上之前所求的next，若匹配失败，则像模式串与父串匹配一样，将指针j移到next【j-1】上。 求next过程实际上只与前一个状态有关： 若不匹配，一直往前退到0或匹配为止 若匹配，则将之前的结果传递： 因为之前的结果不为0时，前后缀有相等的部分，所以j所指的实际是与当前值相等的前缀，可视为将前缀从前面拖了过来，就不必将指针从前缀开始匹配了，所以之前的结果是可以传递的。

使用next数组来做匹配​
let haystack = "AAAAAAAAAAAAAAAAAB"
let needle = "AAAAB"

// 计算前缀表采用第一种方法（不右移也不减一）
const getNext = function (needle) {
    let j = 0;   //j初始值从0，第一位开始
    let next = [];
    next[0] = j;  //数组next[0]为0，首位(单位)字符肯定没有前后缀
    for (let i = 1; i < needle.length; i++) {   //注意i从1开始
        // 前后缀不相同
        while (j > 0 && needle[i] !== needle[j]) {   //j要保证大于0，回退过程中比较前缀尾j与后缀尾i是否相等
            j = next[j - 1];  //j回退到上一位，j到字符串首位还不相等说明当前i作为终止位的字串没有最长相等前后缀，next[i]赋值0
        }
        // 前后缀相同
        if (needle[i] === needle[j]) {
            j++; //相同，j此时指向的是前缀字符串（上一级），要同时向后移动j和i准备下一轮匹配（移动i在for循环里）
        }
        next[i] = j;// 将j（前缀的长度）赋给next[i]
    }
    return next;
}
function getAns(haystack, needle) {
    let next = getNext(needle); //获取前缀表next
    let j = 0; //j指针指向模式串起始位置
    for (let i = 0; i < haystack.length; i++) { //i指向文本串起始位置。
        while (j > 0 && haystack[i] !== needle[j]) //不相同，j就要从next数组里寻找下一个匹配的位置
            j = next[j - 1];
        if (haystack[i] === needle[j]) //如果相同，那么i 和 j 同时向后移动：
            j++; // i的增加在for循环里
        if (j === needle.length) //如果j指向了模式串的末尾，那么就说明模式串完全匹配文本串里的某个子串了。
            return (i - needle.length + 1);//返回当前在文本串匹配模式串的位置i减去模式串的长度，就是文本串字符串中出现模式串的第一个位置
    }
    return -1;//文本串中没有匹配的字串，依题返回-1
}
console.log(getAns(haystack, needle)); //13

关于KMP算法，主要的是理解它的前缀表思想: 拿模板串当前匹配失败的后缀作为下一轮匹配的前缀：这样就省去了匹配公共前后缀片段的必失败轮次 可以带来的对时间复杂度的优化，难点在于如何构造 next数组

7. 整数反转​

7. 整数反转

var reverse = function (x) {
    let y = parseInt(x.toString().split("").reverse().join(""));
    if (x < 0)
        y = - y;
    return y > Math.pow(2, 31) - 1 || y < Math.pow(-2, 31) ? 0 : y;
};

415. 字符串相加​

415. 字符串相加

var addStrings = function(num1, num2) {
    if(num1===num2&&num1==='0')return num1
    num1=num1.split('').reverse()
    num2=num2.split('').reverse()
    const len =Math.max(num1.length,num2.length)
    let flag=0
    const result=[]
    for(let i=0;i<len;i++){
        const n1=+num1[i]||0
        const n2=+num2[i]||0
        let sum=n1+n2+flag
        flag=0
        if(sum>9){
            sum-=10
            flag=1  //进位1
        }
        result.push(sum)
    }
    if(flag) result.push(flag)
    return result.reverse().join("")
};

8. 字符串转换整数 (atoi)​

8. 字符串转换整数 (atoi)

var myAtoi = function (s) {
    let res = 0;
    let maxnum = 2 ** 31 - 1, minnum = (-2) ** 31
        // 正负号，默认正号
        negativeSymbol = 1;
    // 把首尾的空格都去掉
       s = s.trim();
    for (let i = 0; i < s.length; i++) {
        // 负数
        if (i == 0 && s[i] == "-") {
            negativeSymbol = -1;
            continue;
            // 正数
        } else if (i == 0 && s[i] == "+") continue;
        // 因为空格会被转成0，所以要排除空格的情况，也就是说在数字范围内就加上
        if (s[i] >= 0 && s[i] <= 9 && s[i] != " ") {
            res = res * 10 + (s[i] - 0);
            // 为什么在这里就判断呢，因为这里如果就溢出的话，就直接跳出，不需要再后面无意义的计算了
            if (res * negativeSymbol <= minnum  ) return minnum;
            else if (res * negativeSymbol >= maxnum) return maxnum;
        } else break;
    }
    return res * negativeSymbol;
};

14. 最长公共前缀​

14. 最长公共前缀

编写一个函数来查找字符串数组中的最长公共前缀。

如果不存在公共前缀，返回空字符串 ""。

var longestCommonPrefix = function(strs) {
        if(!strs.length) return "";
        res=strs[0]; //选定第一个为基准
        for(str of strs){
            for(let i=0;i<res.length;i++){
                if(str[i]!==res[i]){ //如果不相等
                    res = res.slice(0, i);
                break;
            }
        }
        }
        return res;
};

43. 字符串相乘​

43. 字符串相乘

var multiply = function (num1, num2) {
    if (num1 === '0' || num2 === '0') {
        return '0'
    }
    var l1 = num1.length, l2 = num2.length, p = new Array(l1 + l2).fill(0)
    for (var i = l1; i--;) {
        for (var j = l2; j--;) {
            var tmp = num1[i] * num2[j] + p[i + j + 1]
            p[i + j + 1] = tmp % 10
            p[i + j] += 0 | tmp / 10
        }
    }
    while (p[0] === 0) {
        p.shift()
    }
    return p.join('')
};

链表​

链表操作​

在实现链表时候，通常在链表前面加一个假头，所谓假头，通常也叫作 Dummy Head 或者“哑头”。实际上，就是在链表前面，加上一个额外的结点。此时，存放了 N 个数据的带假头的链表，算上假头一共有 N+1 个结点。

那额外的结点不会存放有意义的数据。那么它的作用是什么呢？

其实，添加假头后，可以省略掉很多空指针的判断，链表的各种操作会变得更加简洁。关于链表的各种操作，主要是以下 6 种基本操作：

  • 链表初始化
  • 尾部追加结点
  • 头部插入结点
  • 查找结点
  • 插入指定位置之前
  • 删除结点

下面以 LeetCode 的707题《设计链表》为例，来实现一下单链表，题目要求将这 6 种基本的操作加以实现：注释中的 /code here/ 部分是填写相应的 6 种功能代码：

var MyLinkedList = function() {
   /* code here: 初始化链表 */
};

MyLinkedList.prototype.addAtTail = function(val) {
  /* code here: 将值为 val 的结点追加到链表尾部 */
};

MyLinkedList.prototype.addAtHead = function(val) {
  /* code here: 插入值val的新结点，使它成为链表的第一个结点 */
};

MyLinkedList.prototype.get = function(index) {
    /* code here: 获取链表中第index个结点的值。如果索引无效，则返回-1 */
  // index从0开始。
};
  
MyLinkedList.prototype.addAtIndex = function(index, val) {
    // code here:
  // 在链表中的第 index 个结点之前添加值为 val  的结点。
  // 1. 如果 index 等于链表的长度，则该结点将附加到链表的末尾。
  // 2. 如果 index 大于链表长度，则不会插入结点。
  // 3. 如果 index 小于0，则在头节点前插入
};

MyLinkedList.prototype.deleteAtIndex = function(index) {
    /* code here: 如果索引index有效，则删除链表中的第index个结点 */
};

（1）链表初始化​

初始化假头链表，首先需要 new 出一个链表结点，并且让链表的 dummy 和 tail 指针都指向它，代码如下：

var listNode = function(val) {
    this.val = val
    this.next = null
};

var MyLinkedList = function() {
    this.dummy = new listNode()
    this.tail = this.dummy
    this.length = 0
};

初始化完成后，链表已经有了一个结点，但是此时，整个链表中还没有任何数据。因此，对于一个空链表，就是指已经初始化好的带假头链表。

虽然 head 和 tail 初始化完成之后，都指向null。但是这两者有一个特点，叫“动静结合”：

  • 静：head 指针初始化好以后，永远都是静止的，再也不会动了。
  • 动：tail 指针在链表发生变动的时候，就需要移动调整。

（2）尾部追加结点​

尾部添加新结点操作只有两步，代码如下：

MyLinkedList.prototype.addAtTail = function(val) {
    // 尾部添加一个新结点
    this.tail.next = new listNode(val)
    // 移动tail指针
    this.tail = this.tail.next;
    // 链表长度+1
    this.length ++
};

带假头的链表初始化之后，可以保证 tail 指针永远非空，因此，也就可以直接去修改 tail.next 指针，省略掉了关于 tail 指针是否为空的判断。

（3）头部插入结点​

需要插入的新结点为 p，插入之后，新结点 p 会成为第一个有意义的数据结点。通过以下 3 步可以完成头部插入：

  • 新结点 p.next 指向 dummy.next；
  • dummy.next 指向 p；
  • 如果原来的 tail 指向 dummy，那么将 tail 指向 p。

对应的代码如下：

MyLinkedList.prototype.addAtHead = function(val) {
    // 生成一个结点，存放的值为val
    const p = new listNode(val)
    // 将p.next指向第一个结点
    p.next = this.dummy.next;
    // dummy.next指向新结点，使之变成第一个结点
    this.dummy.next = p;
    // 注意动静结合原则，添加结点时，注意修改tail指针。
    if (this.tail == this.dummy) {
      this.tail = p;
    }
    // 链表长度+1
    this.length ++
};

这段代码有趣的地方在于，当链表为空的时候，它依然是可以工作的。因为虽然链表是空的，但是由于有 dummy 结点的存在，代码并不会遇到空指针。

注意： 如果链表添加了结点，或者删除了结点，一定要记得修改 tail 指针。如果忘了修改，那么就不能正确地获取链表的尾指针，从而错误地访问链表中的数据。

（4）查找结点​

在查找索引值为 index（假设 index 从 0 开始）的结点时，你需要注意，大多数情况下，返回指定结点前面的一个结点 prev 更加有用。好处有以下两个方面：

  • 通过 prev.next 就可以访问到想要找到的结点，如果没有找到，那么 prev.next 为 null；
  • 通过 prev 可以方便完成后续操作，比如在 target 前面 insert 一个新结点，或者将 target 结点从链表中移出去。

因此，如果要实现 get 函数，应该先实现一个 getPrevNode 函数：

MyLinkedList.prototype.getPreNode = function(index) {
    if (index < 0 || index >= this.length) {
      return -1;
    }
    // 初始化front与back，分别一前一后
    let front = this.dummy.next
    let back = this.dummy
    // 在查找的时候，front与back总是一起走
    for (let i = 0; i < index && front != null; i++) {
      back = front;
      front = front.next;
    }
    // 把back做为prev并且返回
    return back
};

有了假头的帮助，这段查找代码就非常健壮了，可以处理以下 2 种情况：

  • 如果 target 在链表中不存在，此时 prev 返回链表的最后一个结点；
  • 如果为空链表（空链表指只有一个假头的链表），此时 prev 指向 dummy。也就是说，返回的 prev 指针总是有效的。

借助 getPrevNode 函数来实现 get 函数：

MyLinkedList.prototype.get = function(index) {
    // 获取链表中第 index 个结点的值。如果索引无效，则返回-1。
    // index从0开始
    if (index < 0 || index >= this.length) {
      return -1;
    }
    // 因为getPrevNode总是返回有效的结点，所以可以直接取值。
    return this.getPreNode(index).next.val
};

（5）插入指定位置之前​

插入指定位置的前面，有 4 个需求。

  • 如果 index 大于链表长度，则不会插入结点。
  • 如果 index 等于链表的长度，则该结点将附加到链表的末尾。
  • 如果 index 小于 0，则在头部插入结点。
  • 否则在指定位置前面插入结点。

其中，Case 1~3 较容易处理。可以直接写。重点在于 Case 4。现在已经有了 getPrevNode() 函数，就可以比较容易地写出 Case 4 的代码，思路如下：

  • 使用 getPrevNode() 函数拿到 index 之前的结点 pre；
  • 在 pre 的后面添加一个新结点。

以下是具体的 Case 1~4 的操作过程：

MyLinkedList.prototype.addAtIndex = function(index, val) {
  if (index > this.length) {
    // Case 1.如果 index 大于链表长度，则不会插入结点。
    return;
  } else if (index == this.length) {
    // Case 2.如果 index 等于链表的长度，则该结点将附加到链表的末尾。
    this.addAtTail(val);
  } else if (index <= 0) {
    // Case 3. 如果index小于0，则在头部插入结点。
    this.addAtHead(val);
  } else {
    // Case 4.
    // 得到index之前的结点pre
    const pre = this.getPreNode(index);
    // 在pre的后面添加新结点
    const p = new listNode(val);
    p.next = pre.next;
    pre.next = p;
    // 链表长度+1
    this.length++;
  }
};

（6）删除节点​

删除结点操作是给定要删除的下标 index（下标从 0 开始），删除的情况分 2 种：

  • 如果 index 无效，那么什么也不做；
  • 如果 index 有效，那么将这个结点删除。

上面这 2 种情况中，Case 1 比较容易处理，相对要麻烦一些的是 Case 2。要删除 index 结点，最好是能找到它前面的结点。有了前面的结点，再删除后面的结点就容易多了。不过已经有了 getPrevNode 函数，所以操作起来还是很简单的。

以下是具体的操作过程

MyLinkedList.prototype.deleteAtIndex = function(index) {
  // Case 1. 如果index无效，那么什么也不做。
  if (index < 0 || index >= this.length) {
    return;
  }
  // Case 2. 删除index结点
  // step 1. 找到index前面的结点
  const pre = this.getPreNode(index);
  // step 2. 如果要删除的是最后一个结点，那么需要更改tail指针
  if (this.tail == pre.next) {
    this.tail = pre;
  }
  // step. 3 进行删除操作。并修改链表长度。
  pre.next = pre.next.next;
  this.length--;
};

（7）总结​

使用哑结点来实现链表的总代码如下：

        /**
* Initialize your data structure here.
*/
var listNode = function(val) {
    this.val = val
    this.next = null
};

var MyLinkedList = function() {
    this.dummy = new listNode()
    this.tail = this.dummy
    this.length = 0
};


/**
* Get the value of the index-th node in the linked list. If the index is invalid, return -1. 
* @param {number} index
* @return {number}
*/
MyLinkedList.prototype.getPreNode = function(index) {
    if (index < 0 || index >= this.length) {
      return -1;
    }
    // 初始化front与back，分别一前一后
    let front = this.dummy.next
    let back = this.dummy
    // 在查找的时候，front与back总是一起走
    for (let i = 0; i < index && front != null; i++) {
      back = front;
      front = front.next;
    }
    // 把back做为prev并且返回
    return back
};

MyLinkedList.prototype.get = function(index) {
    if (index < 0 || index >= this.length) {
      return -1;
    }
    
    return this.getPreNode(index).next.val
};

/**
* Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. 
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtHead = function(val) {
    // 生成一个结点，存放的值为val
    const p = new listNode(val)
    // 将p.next指向第一个结点
    p.next = this.dummy.next;
    // dummy.next指向新结点，使之变成第一个结点
    this.dummy.next = p;
    // 注意动静结合原则，添加结点时，注意修改tail指针。
    if (this.tail == this.dummy) {
      this.tail = p;
    }
    // 链表长度+1
    this.length ++
};

/**
* Append a node of value val to the last element of the linked list. 
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtTail = function(val) {
    // 尾部添加一个新结点
    this.tail.next = new listNode(val)
    // 移动tail指针
    this.tail = this.tail.next;
    // 链表长度+1
    this.length ++
};

/**
* Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. 
* @param {number} index 
* @param {number} val
* @return {void}
*/
MyLinkedList.prototype.addAtIndex = function(index, val) {
  if (index > this.length) {
    // Case 1.如果 index 大于链表长度，则不会插入结点。
    return;
  } else if (index == this.length) {
    // Case 2.如果 index 等于链表的长度，则该结点将附加到链表的末尾。
    this.addAtTail(val);
  } else if (index <= 0) {
    // Case 3. 如果index小于0，则在头部插入结点。
    this.addAtHead(val);
  } else {
    // Case 4.
    // 得到index之前的结点pre
    const pre = this.getPreNode(index);
    // 在pre的后面添加新结点
    const p = new listNode(val);
    p.next = pre.next;
    pre.next = p;
    // 链表长度+1
    this.length++;
  }
};

/**
* Delete the index-th node in the linked list, if the index is valid. 
* @param {number} index
* @return {void}
*/
  
  
MyLinkedList.prototype.deleteAtIndex = function(index) {
  // Case 1. 如果index无效，那么什么也不做。
  if (index < 0 || index >= this.length) {
    return;
  }
  // Case 2. 删除index结点
  // step 1. 找到index前面的结点
  const pre = this.getPreNode(index);
  // step 2. 如果要删除的是最后一个结点，那么需要更改tail指针
  if (this.tail == pre.next) {
    this.tail = pre;
  }
  // step. 3 进行删除操作。并修改链表长度。
  pre.next = pre.next.next;
  this.length--;
};

/** 
* Your MyLinkedList object will be instantiated and called as such:
* var obj = new MyLinkedList()
* var param_1 = obj.get(index)
* obj.addAtHead(val)
* obj.addAtTail(val)
* obj.addAtIndex(index,val)
* obj.deleteAtIndex(index)
*/

如果不使用哑结点，而直接初始化head，代码如下：

/**
 * Initialize your data structure here.
 */
var MyLinkedList = function() {
  this.head=null
  this.rear=null
  this.len=0
};
function ListNode(val) {
  this.val = val;
  this.next = null;
}
/**
 * Get the value of the index-th node in the linked list. If the index is invalid, return -1. 
 * @param {number} index
 * @return {number}
 */
MyLinkedList.prototype.get = function(index) {
  if(index<0||index>this.len-1)
    return -1
  var node=this.head
  while(index-->0){
    if(node.next==null)
      return -1
    node=node.next
  }
  return node.val
};

/**
 * Add a node of value val before the first element of the linked list. After the insertion, the new node will be the first node of the linked list. 
 * @param {number} val
 * @return {void}
 */
MyLinkedList.prototype.addAtHead = function(val) {
  var node=new ListNode(val)
  if(this.head==null)
    this.rear=node
  else
    node.next=this.head
  this.head=node
  this.len++
};

/**
 * Append a node of value val to the last element of the linked list. 
 * @param {number} val
 * @return {void}
 */
MyLinkedList.prototype.addAtTail = function(val) {
  var node=new ListNode(val)
  if(this.head==null)
    this.head=node
  else
    this.rear.next=node
  this.rear=node
  this.len++
};

/**
 * Add a node of value val before the index-th node in the linked list. If index equals to the length of linked list, the node will be appended to the end of linked list. If index is greater than the length, the node will not be inserted. 
 * @param {number} index 
 * @param {number} val
 * @return {void}
 */
MyLinkedList.prototype.addAtIndex = function(index, val) {
  if(index<=0)
    return this.addAtHead(val)
  if(this.len<index)
    return
  if(index==this.len)
    return this.addAtTail(val)
  var node=this.head
  while(index-->1){
    node=node.next
  }
    
  var newnode=new ListNode(val)
  newnode.next=node.next
  node.next=newnode
  this.len++
};

/**
 * Delete the index-th node in the linked list, if the index is valid. 
 * @param {number} index
 * @return {void}
 */
MyLinkedList.prototype.deleteAtIndex = function(index) {
  if(index<0||index>this.len-1||this.len==0)
    return
  if(index==0){
    this.head=this.head.next
    this.len--
    return
  }

  var node=this.head
  var myindex=index
  while(index-->1){
    node=node.next
  }
  if(myindex==(this.len-1)){
    this.rear=node
  }
  node.next=node.next.next
  this.len--
};

/**
 * Your MyLinkedList object will be instantiated and called as such:
 * var obj = new MyLinkedList()
 * var param_1 = obj.get(index)
 * obj.addAtHead(val)
 * obj.addAtTail(val)
 * obj.addAtIndex(index,val)
 * obj.deleteAtIndex(index)
 */

这两段代码一对比就能看出来，使用哑结点会简洁很多。

206. 反转链表​

206. 反转链表

function ListNode(val, next) {
      this.val = (val===undefined ? 0 : val)
     this.next = (next===undefined ? null : next)
 }

var reverseList = function(head) {
    if(!head||!head.next) return head;
    let item =head;   
    let prev=null;   // prev   item    
    let next=item;
    while(item){
        next=item.next;    //  先把当前head的后一个存起来
        item.next=prev;   //   然后再把head的下一个指向前面  
        prev=item       //  整体后移 相当于进行了迭代 prev现在是之前的item    
        item=next         //    之前的item为item原来的后一个
    }
    return prev
};

92. 反转链表 II​

92. 反转链表 II

给你单链表的头指针 head 和两个整数 left 和 right ，其中 left <= right 。请你反转从位置 left 到位置 right 的链表节点，返回 反转后的链表 。

var reverseBetween = function (head, m, n) {
    // 用来记住整个链表的头节点位置
    let res = new ListNode(0)
    res.next = head
    // 找到需要反转的位置
    let pre = res
    for (let i = 1; i < m; ++i) {
        pre = pre.next
    }
    // 将head指向要反转的链表部分的头部   利用三个节点
    head = pre.next
    for (let i = m; i < n; ++i) {
        let nxt = head.next
        // nxt 节点要被放到反转部分的头部，所以将head的next指向它的下下个节点
        head.next = head.next.next
        // 将nxt放到头部，pre.next指向的是反转部分的头部节点
        nxt.next = pre.next
        // 重新将pre指向反转部分的头部 向前
        pre.next = nxt
    }
    return res.next
};

141. 环形链表​

141. 环形链表

hash表

var hasCycle = (head) => {
    let map = new Map();
    while (head) {
        if (map.has(head)) return true;//如果当前节点在map中存在就说明有环
        map.set(head, true);//否则就加入map
        head = head.next;//迭代节点
    }
    return false;//循环完成发现没有重复节点，说明没环
};

双指针

var hasCycle = function(head) {
    if(head === null) return false
    let slow = head, fast = head.next
    while(fast && fast.next) {
        if (slow.next === fast.next.next) return true
        slow = slow.next
        fast = fast.next.next
    }
    return false
};

142. 环形链表 II​

142. 环形链表 II

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。 如果链表无环，则返回 null。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。

var detectCycle = function (head) {
    // 快慢指针初始化指向 head
    let slow = head;
    let fast = head;
    // 快指针走到末尾时停止
    while (fast && fast.next) {
        // 慢指针走一步，快指针走两步
        slow = slow.next;
        fast = fast.next.next;
        // 快慢指针相遇，说明含有环
        if (slow == fast) {
            // 任一一节点指向头节点
            fast = head;
            // 同步向前进
            while (fast != slow) {
                fast = fast.next;
                slow = slow.next;
            }
            // 返回入口节点
            return fast;
        }
    }
    // 不包含环
    return null;
};

160. 相交链表​

160. 相交链表

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。

假设链表headA和headB长度分别为a,b,相交部分长度为c

让node1和node2作为headA和headB的结点一起向后移动，遍历完自己的链表就去遍历对方的链表

到达第一个交点时

node1走的长度是 a + (b - c) node2走的长度是 b + (a - c) a + (b - c) = b + (a - c)

因为路程相同，又是一起移动的，所以node1和node2会在第一个交点相遇

如果没有交点，node1和node2走的路程是a + b，此时同时到达对方链表的最后一个结点，再移动到next，两个结点都是null，相等，会返回null

var getIntersectionNode = function (headA, headB) {
    let a = headA,
        b = headB;
    while (a != b) {
        // a 走一步，如果走到 headA 链表末尾，转到 headB 链表
        a = a != null ? a.next : headB;
        // b 走一步，如果走到 headB 链表末尾，转到 headA 链表
        b = b != null ? b.next : headA;
    }
    return a;
};

876. 链表的中间结点​

876. 链表的中间结点

给定一个头结点为 head 的非空单链表，返回链表的中间结点。如果有两个中间结点，则返回第二个中间结点。

使用快慢指针来实现，初始化slow和fast两个指针，开始时两个指针都指向头结点。然后慢指针一次走一步，快指针一次走两步，这样快指针走完整个链表时，慢指针正好走到链表的中间。

在遍历的过程中，如果快指针的后一个节点为空，就结束遍历，返回慢指针的值。

var middleNode = function (head) {
    var low = head;
    var fast = head;
    while (fast && fast.next) {
        low = low.next;
        fast = fast.next.next;
    }
    return low;
};

234.回文链表​

234. 回文链表

给你一个单链表的头节点 head ，请你判断该链表是否为回文链表。如果是，返回 true ；否则，返回 false 。

传入head 进行正反处理 最后判断是否相等

var isPalindrome = function (head) {
    let a = '', b = '';
    while (head != null) {
        a = a + head.val;
        b = head.val + b;
        head = head.next;
    }
    return a === b;
};

双指针

首先将链表转为数组，左指针指向第一个节点，右指针指向最后一个节点 比较两个指针指向的节点中的数据，在两个指针相遇之前没有遇到不相等的节点则返回true，否则返回false

var isPalindrome = function(head) {
    let arr = [];
    while(head){
        arr.push(head.val);
        head = head.next;
    }
    let left = 0, right = arr.length-1;
    while(left <= right){
        if(arr[left] != arr[right]) return false;
        left++;
        right--;
    }
    return true;
};

21. 合并两个有序链表​

21. 合并两个有序链表

var mergeTwoLists = function (l1, l2) {
    if (l1 === null) {
        return l2;
    } else if (l2 === null) {
        return l1;
    } else if (l1.val < l2.val) {
        l1.next = mergeTwoLists(l1.next, l2);
        return l1;
    } else {
        l2.next = mergeTwoLists(l1, l2.next);
        return l2;
    }
};

23. 合并K个升序链表​

23. 合并K个升序链表

var mergeKLists = function (lists) {
  // 当是空数组的情况下
  if (!lists.length) {
    return null;
  }
  // 合并两个排序链表
  const merge = (head1, head2) => {
    let dummy = new ListNode(0);
    let cur = dummy;
    // 新链表，新的值小就先接谁
    while (head1 && head2) {
      if (head1.val < head2.val) {
        cur.next = head1;
        head1 = head1.next;
      } else {
        cur.next = head2;
        head2 = head2.next;
      }
      cur = cur.next;
    }
    // 如果后面还有剩余的就把剩余的接上
    cur.next = head1 == null ? head2 : head1;
    return dummy.next;
  };
  const mergeLists = (lists, start, end) => {
    // base case  只有一个链接的情况
    if (start + 1 == end) {
      return lists[start];
    }
    // 输入的k个排序链表，可以分成两部分，前k/2个链表和后k/2个链表
    // 如果将这前k/2个链表和后k/2个链表分别合并成两个排序的链表，再将两个排序的链表合并，那么所有链表都合并了
    let mid = start + ((end - start) >> 1);
    let head1 = mergeLists(lists, start, mid);
    let head2 = mergeLists(lists, mid, end);
    return merge(head1, head2);
  };
  // 前闭后开
  return mergeLists(lists, 0, lists.length);
};

剑指 Offer 22. 链表中倒数第k个节点​

剑指 Offer 22. 链表中倒数第k个节点

先把距离拉开为k 然后再一起往后移动

var getKthFromEnd=function(head,k){
    let slow=head
    while(k--){
        head=head.next
    }
    while(head){
        slow=slow.next
        head=head.next
    }
    return slow

}
var kthToLast = function(head, k) {
    let fast = head
    let slow = head
    // 快指针先走
    while (k !== 0) {
      fast = fast.next
      k--
    }
    // 快慢一起走
    while (fast !== null) {
      fast = fast.next
      slow = slow.next
    }
    return slow.val
};

25. K 个一组翻转链表​

25. K 个一组翻转链表


var reverseKGroup = function (head, k) {
    if (!head) return null;
    let start = head, end = head;

    for (let i = 0; i < k; i++) {
        // 如果在还没遍历到第 k 个，end 空了，即 head 链表个数不满足 k 个，直接返回原链表
        if (!end) {
            return head;
        } else {
            end = end.next;
        }
    }

    let newHead = reverse(start, end); // 左闭右开区间
    start.next = reverseKGroup(end, k); // 翻转以后，原本的 start 指向的结点，变到了 end 的前一个，直接 start.next 继续递归翻转后续的就行
    return newHead;
};

// 反转区间 [a, b) 的元素，注意是左闭右开
function reverse(head, end) {
    let p = head, q, newHead; // p 在前面，q 跟在 p 的后面
    while (p !== end) {
        q = p; // q 赋值会原链表 p 的位置
        p = p.next; // p 继续向后遍历
        q.next = newHead;
        newHead = q;
    }
    return newHead;
};

19. 删除链表的倒数第 N 个结点​

19. 删除链表的倒数第 N 个结点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

先后指针：快指针先走n-1步后慢指针再开始从头节点开始走。当快指针走到最后一个结点的时候，慢指针就走到了倒数第N个结点。

var removeNthFromEnd = function(head, n) {
  // 先指针先走n-1步
  let fast = head;
  for(let i=1; i<=n-1; i++) {
    fast = fast.next;
  }
  let slow = head;
  // 缓存要删除结点的前一个结点
  let pre = null;
  while(fast.next) {
    pre = slow;
    fast = fast.next;
    slow = slow.next;
  }
  // 如果要删除的结点是第一个结点的话，则直接返回slow.next
  if(pre === null) {
    return slow.next;
  }
  else {
    pre.next = slow.next;
  }
  return head;
}

2. 两数相加​

2. 两数相加

给你两个 非空 的链表，表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的，并且每个节点只能存储 一位 数字。

请你将两个数相加，并以相同形式返回一个表示和的链表

var addTwoNumbers = function (l1, l2) {
    let head = null, tail = null;
    let carry = 0;
    while (l1 || l2) {
        const n1 = l1 ? l1.val : 0;
        const n2 = l2 ? l2.val : 0;
        const sum = n1 + n2 + carry;
        if (!head) {
            head = tail = new ListNode(sum % 10);
        } else {
            tail.next = new ListNode(sum % 10);
            tail = tail.next;
        }
        carry = Math.floor(sum / 10);
        if (l1) {
            l1 = l1.next;
        }
        if (l2) {
            l2 = l2.next;
        }
    }
    if (carry > 0) {
        tail.next = new ListNode(carry);
    }
    return head;
};

445. 两数相加 II​

445. 两数相加 II

给你两个 非空 链表来代表两个非负整数。数字最高位位于链表开始位置。它们的每个节点只存储一位数字。将这两数相加会返回一个新的链表。

双栈法

将两个单链表中的数据导出到两个栈中

然后依次同时出栈，相加，保存十位，只留个位，头插到结果链表中

最后判断十位是否还有数字，若有，头插到结果链表中

var addTwoNumbers = function(l1, l2) {
    // 栈
    let stack1 = [], stack2 = [];
    while(l1 || l2) {
        if(l1) {
            stack1.push(l1.val);
            l1 = l1.next;
        }
        if(l2) {
            stack2.push(l2.val);
            l2 = l2.next;
        }
    }
    let res = new ListNode();
    let add = 0;
    while(stack1.length || stack2.length) {
        let num = 0;
        num += (stack1.length) ? stack1.pop() : 0;
        num += (stack2.length) ? stack2.pop() : 0;
        num += add;
        if(num > 9) {
            add = parseInt(num / 10);
            num = num % 10;
        } else {
            add = 0;
        }
        //头插
        let node  = new ListNode(num);
        node.next = res.next;
        res.next = node;
    }
    if(add !== 0) {
        let node  = new ListNode(add);
        node.next = res.next;
        res.next = node;
    }
    return res.next;

};

61. 旋转链表​

61. 旋转链表

给你一个链表的头节点 head ，旋转链表，将链表每个节点向右移动 k 个位置。

输入：head = [1,2,3,4,5], k = 2 输出：[4,5,1,2,3]

img

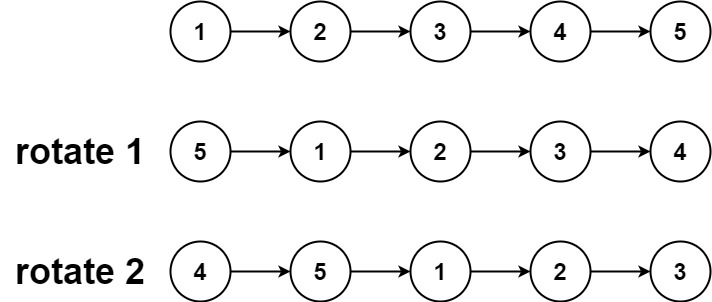
直接的思路就是将单链表转化为一个环形链表，然后移动完成之后再将链表断开为单链表，实现步骤主要是三步：

  • 首先遍历链表，找到链表的尾结点，将尾结点和头结点连起来，这样就形成了一个环形链表；
  • 题目说的右移k步，这里我们让尾结点左移，相当于往左移动length-k步；
  • 最后，移动完成之后，找到链表的尾结点，将环形链表断开为单向链表。
var rotateRight = function(head, k) {
    if(!head || !head.next){
        return head
    }
    // 找到尾结点，将单链表形成环形链表
    let tail = head
    let length = 1
    while(tail.next){
        length++
        tail = tail.next
    }
    tail.next = head
    // 尾结点进行移动
    k = k % length
    for(let i = 1; i <= length - k; i++){
        tail = tail.next
    }
    // 找到头结点，断开环形链表
    head = tail.next
    tail.next = null
    return head
};
var rotateRight = function (head, k) {
    if (!head || k === 0) {
        return head
    }
    let cur = head
    let length = 0
    while (cur) {
        length++
        cur = cur.next
    }
    k = k % length
    if (k === 0) {
        return head
    }
    let pre = {
        next: head
    }
    let t = k
    while (t < length) {
        pre = pre.next
        t++
    }
    //差距为k

    //然后再次遍历  对pre节点末尾的下一个设置为head
    const newHead = pre.next
    pre.next = null
    pre = newHead
    while (pre.next) {
        pre = pre.next
    }
    pre.next = head
    return newHead
};

24. 两两交换链表中的节点​

24. 两两交换链表中的节点

给你一个链表，两两交换其中相邻的节点，并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题（即，只能进行节点交换）。

递归

var swapPairs = function(head) {
    if(!head||!head.next) return head;
    let firstNode = head;
    let secondNode = head.next;
    firstNode.next = swapPairs(secondNode.next)
    secondNode.next = firstNode;
    return secondNode;
};

交换反转

function ListNode(val, next) {
    this.val = (val===undefined ? 0 : val)
    this.next = (next===undefined ? null : next)
 }
var swapPairs=function (head){
    let ret=new ListNode(0,head),temp=ret;
    while(temp.next&&temp.next.next){
        let cur=temp.next.next,pre=temp.next;
        pre.next=cur.next;  //1的下一个变成3
        cur.next=pre        //2的下一个变成1
        temp.next=cur;          //进行迭代  [temp,temp.next]=[pre,cur]
        temp=pre;                       

    }
    return ret.next;
}

1721. 交换链表中的节点​

1721. 交换链表中的节点

给你链表的头节点 head 和一个整数 k 。

交换 链表正数第 k 个节点和倒数第 k 个节点的值后，返回链表的头节点（链表 从 1 开始索引）。

先把差距定为k 然后保存前面的 然后开始移动 前节点移动到末尾则可以得到倒数第k个节点

var swapNodes = function (head, k) {
  // 设置计数器
  let count = 1
  // 设置遍历指针
  let p = head
  // 定义第K个节点
  let front = null
  // 定义倒数第K个节点
  let back = head
  while (p) {
    // count = k 是， p为第 K 个节点
    if (count === k) {
      // 找到第K个节点
      front = p
    }
    // 当 count > k 时， back 指针开始移动
    if (count > k) {
      back = back.next
    }
    p = p.next
    count++
  }
  // 交换节点 val
  let temp = front.val
  front.val = back.val
  back.val = temp

  // 完成 return
  return head
};

86. 分隔链表​

86. 分隔链表

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当 保留 两个分区中每个节点的初始相对位置。

分隔链表 ，定义俩个链表 smaller(小于特定值) greater(大于特定值) 遍历一次将初始链表中所有值加入所定义的俩个链表中(遍历 所以相对位置不会改变) 最后将俩个链表连起来. 有个小技巧就是在初始定义smaller和greater链表时定义了它们的引用dummy...，并且头结点值为-1, 在连接链表的时候就用它们的引用来连接。

var partition = function(head, x) {
  var smaller = dummySmaller = new ListNode(-1);  //-1 正数?
  var greater = dummyGreater = new ListNode(-1);
  while (head) {
    // console.log(head.val);
    // 链表的遍历
    if (head.val < x) {
      smaller.next = head; //进入较小值分区
      smaller = smaller.next; //更新smaller
    } else {
      greater.next = head;
      greater = greater.next;
    }
    head = head.next;
  }
  // 俩个分区合并
  smaller.next = dummyGreater.next; 
  greater.next = null;
  return dummySmaller.next;  //返回分隔后的头节点
}

双指针 x=3

1->4->3->2->5->2

1->2->2->4->3->5

var partition = function(head, x) {
    if (!head || !head.next)
        return head; // 边界处理
    let newhead = new ListNode(null);
    newhead.next = head; // 新增一个头节点
    let q = newhead,p,flag = true; // 记录第一个大于等于x的节点
    while (q.next) {
        if (flag) { // 如果没找到大于等于x的节点，寻找该节点p
            if (q.next.val >= x) {
                p = q;  //记录大于x节点的前一个
                flag = false;
            }
            q = q.next;
        } else { // 否则遍历寻找小于x的节点插入p之后，
            if (q.next.val < x) { 
                let s = q.next; // 暂存小节点s
                q.next = s.next; // 删除节点s q指向s的下一个
                s.next = p.next; //在p后插入小节点s  
                p.next = s;  //小节点的下一个指向s
                p = s;  // p更新指向新插入的节点 往后移动
            } else
                q = q.next;
        }
    }
    return newhead.next;
};

143. 重排链表​

143. 重排链表

给定一个单链表 L 的头节点 head ，单链表 L 表示为：

L0 → L1 → … → Ln - 1 → Ln 请将其重新排列后变为：

L0 → Ln → L1 → Ln - 1 → L2 → Ln - 2 → … 不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

var reorderList = function(head) {
    if(!head.next) return head;

    let slow = head, fast = head.next; // slow 为第一个结点开始，fast 为第二个结点开始，这样结点总个数奇数或偶数都很好兼容
    // fast 走两步，不能一次性走两步，要一步一步走
    while(fast && fast.next) {
        slow = slow.next;
        fast = fast.next;
        // 对于 fast 第二步，需要先判断，如果 fast 后面还可以再走一步，才往后走
        if(fast.next) {
            fast = fast.next;
        }
    }

    // 现在 slow 和 fast 之间就是要翻转的部分了 (slow, fast]
    let newHead = null, p = slow.next, q;
    slow.next = null; // 前半部分和后半部分断开联系
    while(p) {
        q = p;
        p = p.next;
        q.next = newHead;
        newHead = q;
    }

    // 现在 newHead 就是后半段翻转后的样子，然后接下来跟前半部分 依次 插入新链表
    let resultHead = new ListNode(0), now = resultHead, flag = true;
    slow = head, fast = newHead;
    while(slow || fast) {
        // 通过 flag 控制现在插入 前半部分 还是 后半部分
        if(flag) {
            now.next = slow;
            slow = slow.next;
        } else {
            now.next = fast;
            fast = fast.next;
        }
        now = now.next;
        flag = !flag;
    }
    return resultHead.next;
};

148. 排序链表​

148. 排序链表

题目要求在O(n log n) 时间复杂度和常数级空间复杂度下对链表进行排序，恰好归并排序可以满足要求。

其主要思路如下：

  • 先判断链表是否只有一个元素，若是则直接返回
  • 使用快慢指针，找到链表的中间节点
  • 对链表的前半部分和后半部分分别递归的进行归并排序
  • 最后将两个子链表进行合并
var sortList = function(head) {
    // 若为空链表或只有一个节点，就直接返回
    if(head === null || head.next === null){
        return head
    }
    // 使用快慢指针获取链表的中间值
    let fast = head
    let slow = head
    while(slow.next && fast.next && fast.next.next){
        slow = slow.next
        fast = fast.next.next
    }
    // 将链表分成两个
    const middle = slow.next
    slow.next = null
    
    // 对左右的两个链表分别递归的进行归并排序
    const left = head
    const right = middle
    return merge(sortList(left), sortList(right))
};

function merge (left, right) {
    // 初始化一个空的结果节点
    let res = new ListNode(null);
    // 当前节点
    let prev = res;   
    while (left && right) {
        // 如果左边的值小于右边的值，当前节点指向左节点，左节点指向下一个节点
        if (left.val < right.val) {
            [prev.next, left] = [left, left.next]
        }else {
        // 如果右边的值小于左边的值，当前节点指向右节点，右节点指向下一个节点
            [prev.next, right] = [right, right.next];
        }
        // 当前节点指向下一个节点
        prev = prev.next;
    }
    // 如果还有剩余的节点，就直接拼接在结果链表的最后
    prev.next = left ? left : right;
    return res.next;
}

借助数组实现

var sortList = function(head) {
    if(head === null || head.next === null){
        return head
    }
    let cur = head
    let index = 0
    const arr = []
    // 将链表转化为数组
    while(cur){
        arr[index] = cur.val
        cur = cur.next
        index ++
    }
    // 对数组进行排序
    arr.sort((a,b) => a-b)
    // 将数组转化为链表
    cur = head
    index = 0
    while(cur){
        cur.val = arr[index]
        index ++
        cur = cur.next
    }
    return head
};

203. 移除链表元素​

203. 移除链表元素

给你一个链表的头节点 head 和一个整数 val ，请你删除链表中所有满足 Node.val == val 的节点，并返回 新的头节点 。

对于这道题目，本身是很简单的，就是遍历链表，删除指定的值，但是需要注意，如果是需要删除的值在链表中时，直接删除即可，如果要删除的节点在链表的头部，这就要处理遍历情况，为了避免这种情况，我们可以初始化一个哑结点dummyHead，它是一个空节点，将他放在头结点的前面。这样就不会出现为空的情况。

var removeElements = function(head, val) {
    let dummyHead = new ListNode(0)
    dummyHead.next = head

    let pre = dummyHead, cur = head
    while(cur){
        cur.val == val ? pre.next = cur.next : pre = cur
        cur = cur.next
    }
    return dummyHead.next
};

82. 删除排序链表中的重复元素II​

82. 删除排序链表中的重复元素 II

给定一个已排序的链表的头 head ， 删除原始链表中所有重复数字的节点，只留下不同的数字 。返回 已排序的链表 。

慢指针指向已确认的无重复元素的最后一项，快指针初始状态下指向慢指针的next，内循环后应该指向重复元素的最后一项。

若内循环退出后，快指针仍然指向next，说明此处没有重复元素，两个指针同时后移。

var deleteDuplicates = function(head) {
    let dummy = {next: head};
    let fast = head, slow = dummy;
    while(fast){
        while(fast.next && fast.next.val == fast.val){
            fast = fast.next;
        }
        if(slow.next != fast){
            slow.next = fast.next;
        }else{
            slow = slow.next;
        }
        fast = fast.next;
    }
    return dummy.next;
};

83. 删除排序链表中的重复元素​

83. 删除排序链表中的重复元素

给定一个已排序的链表的头 head ， 删除所有重复的元素，使每个元素只出现一次 。返回 已排序的链表 。

我们只要对比两个相邻的节点，如果值相等，就将删除一个元素，如不相等就直接向后移动指针，重复行上述步骤，直到遍历完链表的所有节点为止。

var deleteDuplicates = function(head) {
    let cur = head

    while(cur && cur.next){
        if(cur.val === cur.next.val){
            cur.next = cur.next.next
        }else{
            cur = cur.next
        }
    }
    return head
};

138. 复制带随机指针的链表​

138. 复制带随机指针的链表

给你一个长度为 n 的链表，每个节点包含一个额外增加的随机指针 random ，该指针可以指向链表中的任何节点或空节点。

构造这个链表的 深拷贝。 深拷贝应该正好由 n 个 全新 节点组成，其中每个新节点的值都设为其对应的原节点的值。新节点的 next 指针和 random 指针也都应指向复制链表中的新节点，并使原链表和复制链表中的这些指针能够表示相同的链表状态。复制链表中的指针都不应指向原链表中的节点。

例如，如果原链表中有 X 和 Y 两个节点，其中 X.random --> Y 。那么在复制链表中对应的两个节点 x 和 y ，同样有 x.random --> y 。 返回复制链表的头节点。

用一个由 n 个节点组成的链表来表示输入/输出中的链表。每个节点用一个 [val, random_index] 表示：

  • val：一个表示 Node.val 的整数。
  • random_index：随机指针指向的节点索引（范围从 0 到 n-1）；如果不指向任何节点，则为 null 。

你的代码 只 接受原链表的头节点 head 作为传入参数。

1）第一步，根据遍历到的原节点创建对应的新节点，每个新创建的节点是在原节点后面，比如下图中原节点1不再指向原原节点2，而是指向新节点1 image-20221006230523415

2）第二步是最关键的一步，用来设置新链表的随机指针 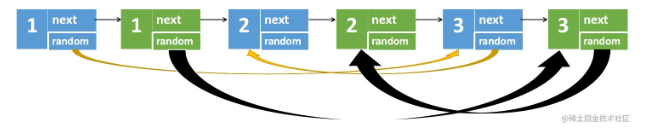image-20221006230534618

上图中，可以看到一个规律

  • 原节点1的随机指针指向原节点3，新节点1的随机指针指向的是原节点3的next
  • 原节点3的随机指针指向原节点2，新节点3的随机指针指向的是原节点2的next

也就是，原节点i的随机指针(如果有的话)，指向的是原节点j。那么新节点i的随机指针，指向的是原节点j的next。

3）第三步只要将两个链表分离开，再返回新链表就可以了 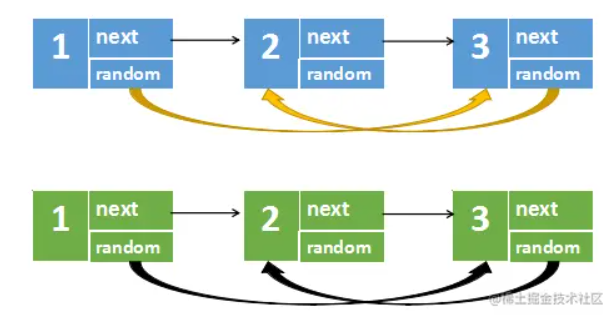image-20221006230546126

/**
 * // Definition for a Node.
 * function Node(val, next, random) {
 *    this.val = val;
 *    this.next = next;
 *    this.random = random;
 * };
 */

/**
 * @param {Node} head
 * @return {Node}
 */
var copyRandomList = function(head) {
    if(!head){
        return null
    }

    let p = head
    // 在每个原节点后面创建一个新节点
    while(p !== null){
        let newNode = new Node(p.val)
        newNode.next = p.next
        p.next = newNode
        p = newNode.next
    }
    p = head
    // 设置新节点的随机节点
    while(p !== null){
        if(p.random){
            p.next.random = p.random.next
        }
        p = p.next.next
    }
    let dummyHead = new Node(-1)
    p = head
    let cur = dummyHead
    // 将两个链表分离
    while(p !== null){
        cur.next = p.next
        cur = cur.next
        p.next = cur.next
        p = p.next
    }
    return dummyHead.next
};

147. 对链表进行插入排序​

147. 对链表进行插入排序

插入排序算法：

  1. 插入排序是迭代的，每次只移动一个元素，直到所有元素可以形成一个有序的输出列表。
  2. 每次迭代中，插入排序只从输入数据中移除一个待排序的元素，找到它在序列中适当的位置，并将其插入。
  3. 重复直到所有输入数据插入完为止。

对于单向链表而言，只有指向后一个节点的指针，因此需要从链表的头节点开始往后遍历链表中的节点，寻找插入位置。对链表进行插入排序的具体过程如下:

  1. 首先判断给定的链表是否为空，若为空，则不需要进行排序，直接返回。
  2. 创建哑节点 dummyHead，令 dummyHead.next = head。引入哑节点是为了便于在 head 节点之前插入节点。
  3. 维护 last 为链表的已排序部分的最后一个节点，初始时 last = head。
  4. 维护 cur 为待插入的元素，初始时 cur = head.next。
  5. 比较 last 和 cur 的节点值。
  • 若 last.val <= cur.val，说明 cur 应该位于 last 之后，将 last后移一位，curr 变成新的 last。
  • 否则，从链表的头节点开始往后遍历链表中的节点，寻找插入 cur 的位置。令 pre 为插入 cur 的位置的前一个节点，进行如下操作，完成对 cur 的插入：
last.next = cur.next
cur.next = pre.next
pre.next = cur
  1. 令 cur = last.next，此时 cur 为下一个待插入的元素。
  2. 重复第 5 步和第 6 步，直到 cur 变成空，排序结束。
  3. 返回 dummyHead.next，为排序后的链表的头节点。
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var insertionSortList = function(head) {
    if(!head){
        return head
    }
    const dummyHead = new ListNode(0)
    dummyHead.next = head

    let last = head, cur = head.next

    while(cur){
        if(last.val <= cur.val){
            last = last.next
        }else{
            let pre = dummyHead
            while(pre.next.val <= cur.val){
                pre = pre.next
            }
            last.next = cur.next
            cur.next = pre.next
            pre.next = cur
        }
        cur = last.next
    }
    return dummyHead.next
};

328. 奇偶链表​

328. 奇偶链表

给定单链表的头节点 head ，将所有索引为奇数的节点和索引为偶数的节点分别组合在一起，然后返回重新排序的列表。

第一个节点的索引被认为是 奇数 ， 第二个节点的索引为 偶数 ，以此类推。

这道题目的思路就是遍历链表，将链表的中的所有的元素分为a和b两个链表，分别用来保存奇数值和偶数值，遍历结束之后，偶数链表拼接在奇数链表后面。具体实现过程如下：

  • 首先将链表节点数为0，1，2的情况排除掉，直接返回head
  • 定义a和b两个链表，分别表示奇数和偶数节点，用node来暂时保存b链表的头结点，便于后面拼接
  • 使用while循环对a和b链表进行交叉遍历赋值。a和b一直指向奇数链和偶数链的最后一个节点
  • 将两个链表进行拼接，并返回
/**
 * Definition for singly-linked list.
 * function ListNode(val, next) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.next = (next===undefined ? null : next)
 * }
 */
/**
 * @param {ListNode} head
 * @return {ListNode}
 */
var oddEvenList = function(head) {
    if(head === null || head.next === null || head.next.next === null){
        return head
    }
    let a = head       // 存放奇数节点
    let b = head.next  // 存放偶数节点
    const node = head.next   // 记录b链表的头节点
    while(b !== null && b.next !== null){
        a.next = b.next
        a = a.next
        b.next = a.next
        b = b.next
    }
    a.next = node
    return head
};

817. 链表组件​

817. 链表组件

给定链表头结点 head，该链表上的每个结点都有一个唯一的整型值。同时给定列表 nums，该列表是上述链表中整型值的一个子集。

返回列表 nums 中组件的个数，这里对组件的定义为：链表中一段最长连续结点的值（该值必须在列表 nums 中）构成的集合。

var numComponents = function(head, G) {
    let cur = head
    let isComponent = false
    let res = 0

    while(cur){
        if(G.indexOf(cur.val) > -1){
            if(!isComponent){
                isComponent = true
                res++
            }
        }else{
            isComponent = false
        }
        cur = cur.next
    }
    return res
};

二叉树​

前中后序遍历(速记323)​

前序遍历​

var preorderTraversal = function(root) {
    const res =[];
    const stack = [];
    while (root || stack.length){
      while(root){
        res.push(root.val);
        stack.push(root);
        root = root.left;
      }
      root = stack.pop();
      root = root.right;
    }
    return res;
};
// 迭代的写法：
var preorderTraversal = function(root) {
  if(!root){
       return [];
    }
    var result = []
    var stack = [root]
    while(stack.length!==0){
       var top = stack.pop();
       if(top.right){
          stack.push(top.right);
       }
       if(top.left){
          stack.push(top.left);
       }
       result.push(top.val);
    }
    return result;
};

// 递归的写法：
var preorderTraversal = function(root) {
  if(!root){
    return [];
  }
  var result = []
  var preorderTraversalNode = (node) => {
      if(node) {
          result.push(node.val)
          preorderTraversalNode(node.left)
          preorderTraversalNode(node.right)
       }
   }
  preorderTraversalNode(root)
  return result
};

中序遍历​

const inorderTraversal = (root) => {
    if(!root) return [];
  const res = [];
  const stack = [];
  while(root || stack.length){
      while(root){
          stack.push(root)
          root = root.left;
      }
     root = stack.pop();
     res.push(root.val);
     root = root.right;
  }
  return res;
};

// 递归的实现
var inorderTraversal = function(root) {
    if(!root){
       return [];
    }
    var result = []
    var inorderTraversalNode = (node) => {
        if(node) {  
            inorderTraversalNode(node.left)
            result.push(node.val)
            inorderTraversalNode(node.right)
         }
     }
    inorderTraversalNode(root)
    return result
};

后序遍历​

var postorderTraversal = function(root) {
    const res =[];
    const stack = [];
    while (root || stack.length){
      while(root){
        stack.push(root);
        res.unshift(root.val);
        root = root.right;
      }
      root = stack.pop();
      root = root.left;
    }
    return res;
};

// 迭代的实现：
var postorderTraversal = function(root) {
    if(!root){
       return [];
    }
    var result = []
    var stack = [root]
    while(stack.length!==0){
       var top = stack.pop();
       result.unshift(top.val);
       if(top.left){
          stack.push(top.left);
       }
       if(top.right){
          stack.push(top.right);
       }
     
    }
    return result;
};

// 递归的实现
var postorderTraversal = function(root) {
    if(!root){
       return [];
    }
    var result = []
    var postorderTraversalNode = (node) => {
        if(node) {  
            postorderTraversalNode(node.left)
            result.push(node.val)
            postorderTraversalNode(node.right)
         }
     }
    postorderTraversalNode(root)
    return result
};

102. 二叉树的层序遍历​

102. 二叉树的层序遍历

var levelOrder = function(root) {
    let res=[],queue=[]
    queue.push(root)
    if(root===null){
        return res
    }
    while(queue.length!==0){
        let length=queue.length
        let curLevel=[]
        for(let i=0;i<length;i++){
            let node=queue.shift()
            curLevel.push(node.val)
            node.left&&queue.push(node.left)
            node.right&&queue.push(node.right)
        }
        res.push(curLevel)
    }
    return res;
};

107. 二叉树的层序遍历 II​

107. 二叉树的层序遍历 II

给你二叉树的根节点 root ，返回其节点值 自底向上的层序遍历 。 （即按从叶子节点所在层到根节点所在的层，逐层从左向右遍历）

DFS

var levelOrderBottom = function(root) {
    let res = []
    let queue = []
    if (root) {
        let level = 0
        queue.push({ node: root, level })
        while (queue.length) {
            const item = queue.shift()
            const node = item.node
            const level = item.level
            if (level === res.length) {
                res.unshift([])
            }
            res[0].push(node.val)
            node.left && queue.push({ node: node.left, level: level + 1 })
            node.right && queue.push({ node: node.right, level: level + 1 })
        }
    }
    return res
};

BFS

var levelOrderBottom = function(root) {
    const res = []
    if (root) {
        const queue = [root]
        while (queue.length) {
            const len = queue.length
            const temp = []
            for (let i = 0; i < len; i++) {
                const node = queue.shift()
                temp.push(node.val)
                node.left && queue.push(node.left)
                node.right && queue.push(node.right)
            }
            res.unshift(temp)
        }
    }
    return res
};

103. 二叉树的锯齿形层序遍历​

103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的 锯齿形层序遍历 。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

使用广度优先遍历的方式，始终从左往右遍历，然后锯齿形的结果通过结果的从前压入和从后压入实现。

var zigzagLevelOrder = function(root) {
    let queue = []
    let ans = []
    let level = 0

    // 空树，直接返回ans
    if(root == null) {
        return ans
    }

    queue.push(root)

    while(queue.length) {
        let length = queue.length
        let isToLeft = level % 2 == 1 // 顺序是否从右到左
        let levelList = []

        for(let i = 0 ; i < length; ++ i) {
            let node = queue.shift() // 和普通的广度优先遍历一样使用队列，先进先出
            console.log('node: ', node)

            isToLeft
            ? levelList.unshift(node.val) // 该层从右往左，从数组前面压入node.val
            : levelList.push(node.val) // 该层从左往右，从数组前面压入node.val

            // 子节点仍然和普通的广度优先遍历一样，从左往右压入队列中
            if(node.left != null) {
                queue.push(node.left)
            }
            if(node.right != null) {
                queue.push(node.right)
            }
        }

        ans[level++] = levelList // 保存该层结果，level自增1
        

    }

    return ans

};

958. 二叉树的完全性检验​

958. 二叉树的完全性检验

完全二叉树通过层序遍历最后的子节点都是null 如果出现了null但又出现了真实节点，直接返回false

var isCompleteTree = function(root) {
    let queue=[root];
        let end=false
        while(queue.length){
            let size=queue.length;
            for(let i=0;i<size;i++){
                let cur=queue.shift()
                if(cur==null) end=true
                else{
                    if(end) return false
                    queue.push(cur.left)
                    queue.push(cur.right)
                }
            }
        }
        return true
};

124. 二叉树中的最大路径和​

124. 二叉树中的最大路径和

const maxPathSum = (root) => {
    let maxSum = Number.MIN_SAFE_INTEGER;//初始化最大路径和

    const dfs = (root) => {
        if (root == null) {//遍历节点是null 返回0
           return 0;
        }
        const left = dfs(root.left);   //递归左子树最大路径和
        const right = dfs(root.right); //递归右子树最大路径和
        maxSum = Math.max(maxSum, left + root.val + right);      //更新最大值
        //返回当前子树的路径和 分为走左边、右边、不动 3种情况
        const pathSum = root.val + Math.max(0, left, right);
        return pathSum < 0 ? 0 : pathSum;
    };
    dfs(root);
    return maxSum; 
};

112. 路径总和​

112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

DFS深度优先遍历​

1.定义一个res为false 2.进行dfs深度遍历 一直向下找 找到叶子节点并且之前经过的节点路径和==targetSum时便改变res为true 3.返回res 如果有符合的路径和那么res就会被改变返回值为true 如果没有路径和那么返回的就是一开始的res=false

var hasPathSum = function(root, targetSum) {
        if(!root) return 0
        let res = false
        const dfs = (root,sum)=>{
        if(!root) return
        if(sum==targetSum && (!root.left && !root.right) ){
            res = true
        }
        if(root.left)  dfs(root.left,sum+root.left.val)
        if(root.right)  dfs(root.right,sum+root.right.val)
        }
        dfs(root, root.val)
        return res
};

时间复杂度为O(n) 因为深度遍历了节点 空间复杂度为O(n) 这里使用了递归存在函数调用堆栈 n就是这个栈的高度 在最坏的情况下n为n 最好的情况下n为logn

var hasPathSum = function(root, targetSum) {
    const traversal = (node, cnt) => {
        if(cnt===0&&!node.left&&!node.right) return true
        if(!node.left&&!node.right) return false
        if(node.left&&traversal(node.left,cnt-node.left.val)) return true
        if(node.right&&traversal(node.right,cnt-node.right.val)) return true
        return false

    }
    if(!root) return false
    return traversal(root,targetSum-root.val)
};

BFS广度优先遍历​

1.进行bfs时 使用队列保存到达每一个节点时的路径和 如果该路径和恰好等于targetSum并且无子节点那么就输出true 2.如果循环结束后都没有return true 那么说明没有路径和等于targetSum 直接在最后返回false

var hasPathSum = function(root, targetSum) {
    if (!root) return 0
    const stack = [[root, root.val]]
    while (stack.length) {
        const [p,l] = stack.shift()
        if(l == targetSum && !p.left && !p.right ) return true
        if (p.left) stack.push([p.left,l+p.left.val])
        if (p.right) stack.push([p.right, l+p.right.val])
    }
    return false
};

递归​

观察我们可以发现 targetSum应该等于根节点的val加上其某条路径上面的所有子节点的val和 故依次递推如果存在某条路径和等于targetSum 那么这条路径上面的叶子节点的值应该等于targetSum减去除叶子节点外的节点值之和

var hasPathSum = function(root, targetSum) {
    if(!root) return false
    if(targetSum==root.val&&!root.left&&!root.right) return true
    return hasPathSum(root.left,targetSum-root.val) || hasPathSum(root.right,targetSum-root.val)
};

129. 求根节点到叶节点数字之和​

129. 求根节点到叶节点数字之和

var sumNumbers = function(root) {
    const dfs=(root,path)=>{
        if(root==null) return 0;
        path=path*10+root.val
        if(!root.left&&!root.right) return path
        return dfs(root.left,path)+dfs(root.right,path)
    }
    return dfs(root, 0);
};

105. 从前序与中序遍历序列构造二叉树​

105. 从前序与中序遍历序列构造二叉树

var buildTree = (preorder, inorder) => {

  //当preorder和inorder均为空的时候说明已经到了空节点
  if (!preorder.length || !inorder.length) return null;

  //创建根节点 -> preorder[0]
  let node = new TreeNode(preorder[0]);

  //找到preoder[0]对应inorder中的位置
  let index = inorder.indexOf(preorder.shift());

  //左右子树递归
  node.left = buildTree(preorder, inorder.slice(0, index));
  node.right = buildTree(preorder, inorder.slice(index + 1));

  //返回根节点
  return node;
};

230. 二叉搜索树中第K小的元素​

230. 二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

使用中序遍历二叉搜索树，得到升序排序数组，然后直接返回数组中第k小的元素即可

var kthSmallest = function(root, k) {
    const res = [];
    // 看到是二叉搜索树应该想到使用中序遍历得到树节点排序好的升序数组
    function traversal(node){
        if (node){
            traversal(node.left);
            res.push(node.val);
            traversal(node.right);
        }
    }
    traversal(root);
    // 输出升序数组第k个最小的元素 下标为 k - 1
    return res[k - 1];
};

543. 二叉树的直径​

543. 二叉树的直径

给定一棵二叉树，你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点

经过一个node，其左右子树的最大深度之和 + 1（二叉树的根节点深度为0） 定义一个递归函数 depth(node) 计算 node 为起点的 路径经过节点数 res 函数返回该节点为 根的子树的深度

时间复杂度：O(n) n为二叉树的节点 遍历n 空间复杂度：O(Height) 常数变量 递归的深度为二叉树的高度

var diameterOfBinaryTree = function(root) {
    let res = 0
    depth(root)
    return res
    function depth (node) {
        if (!node) return 0 // 节点不存在返回0
        let left = depth(node.left) // left为左子树的深度
        let right = depth(node.right)//right 为右子树的深度
        res = Math.max(left + right, res) //计算l+r 更新res
        return Math.max(left, right)+1 //返回该节点为根的子树的深度
    }
};

101. 对称二叉树​

101. 对称二叉树

递归

var isSymmetric = function (root) {
    if(!root) return true;
    const isMirror=(l,r)=>{
        if(!l&&!r) return true;
        if(l&&r){
            if(l.val===r.val&&isMirror(l.left,r.right)&&isMirror(l.right,r.left)){
                return true
            }
        }
        return false
    }

    return isMirror(root.left,root.right)
}

BFS

维护一个队列，起初，根节点（如果存在）的左右子树入列 每次出列一对节点，考察它们俩是否对称 如果不对称，那整个树就不对称，结束BFS，如果对称，则下一对节点入列 哪些情况不对称： 一个为 null 一个不为 null，直接返回 false 都存在，但 root 值不同，直接返回 false

const isSymmetric = (root) => {
  if (root == null) return true; 

  const queue = [];
  queue.push(root.left, root.right);  // 起初入列两个子树

  while (queue.length) {  // 队列清空就结束，没有节点可入列了
    const levelSize = queue.length; // 当前层的节点个数
    for (let i = 0; i < levelSize; i += 2) { // 当前层的节点成对出列
      const left = queue.shift();   
      const right = queue.shift();  // 出列一对节点
      if ((left && right == null) || (left == null && right)) { // 一个存在 一个不存在
        return false;
      }
      if (left && right) { // 两个都存在
        if (left.val != right.val) { // 节点值不同，不对称
          return false;
        }
        queue.push(left.left, right.right); // 推入下一层的一对节点
        queue.push(left.right, right.left); // 推入下一层的一对节点
      }
    }
  }
  return true; // bfs结束，始终没有返回false，则返回真
};
var isSymmetric = function(root) {
  let stack = [];
  if (!root) return true;
  stack.push(root.left, root.right);
  while (stack.length > 0) {
    const right = stack.pop();
    const left = stack.pop();
    if (left === null && right === null) {
      // 节点为空什么都不做
    } else if (left && right && left.val === right.val) {
      //左左节点和对称右右节点入栈
      stack.push(left.left);
      stack.push(right.right);
      //左右节点和对称右左节点入栈
      stack.push(left.right);
      stack.push(right.left);
    } else {
      return false;
    }
  }
  return true;
};

栈模拟递归

var isSymmetric = (root) => {
  if (!root) return true
  let leftStack = [], rightStack = [] // 维护两个栈
  let curLeft = root.left             // 当前的左子树
  let curRight = root.right           // 当前的右子树
  while (curLeft || curRight || leftStack.length || rightStack.length) {
    while (curLeft) {         // 左子树存在
      leftStack.push(curLeft) // 推入leftStack栈
      curLeft = curLeft.left  // 不断将左子树入栈
    }
    while (curRight) {          // 右子树存在
      rightStack.push(curRight) // 推入rightStack栈
      curRight = curRight.right // 不断将右子树压入栈
    }
    if (leftStack.length !== rightStack.length) return false
                                // 栈的高度不相等，说明结构不对称
    curLeft = leftStack.pop()   // 栈顶节点出栈，赋给curLeft
    curRight = rightStack.pop() // 栈顶节点出栈，赋给curRight
    if (curLeft.val !== curRight.val) return false
                                // 两个栈出栈的节点值不相等 不对称
    curLeft = curLeft.right     // 考察左子树的right
    curRight = curRight.left    // 考察右子树的left
  }
  return true
}

100. 相同的树​

100. 相同的树

DFS

function isSameTree(p, q) {
    if (p == null && q == null) {
        return true;
    }
    if (p == null || q == null) {
        return false
    }
    if (p.val !== q.val) {
        return false
    }

    return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
};

BFS

把树节点分别加入队列, 看出队的节点是否一样即可

var isSameTree = function(p, q) {
  let pQ = [p]
  let qQ = [q]
  while(pQ.length && qQ.length){
    let pc = pQ.shift()
    let qc = qQ.shift()
    if(pc && qc && pc.val != qc.val || (!pc && qc || pc && !qc)) return false
    if(pc){
      pQ.push(pc.left)
      pQ.push(pc.right)
    }
    if(qc){
      qQ.push(qc.left)
      qQ.push(qc.right)
    }
  }
  return true
};

序列化

var isSameTree = function(p, q) {
  return JSON.stringify(p) === JSON.stringify(q)
};

637. 二叉树的层平均值​

637. 二叉树的层平均值

DFS先递归后计算

将节点和层数作为递归参数，递归终止条件为当前节点不存在。

var averageOfLevels = function(root) {
    const helper = (root, level) => {
        // 如果为空那么结束递归
        if (!root) {
            return
        }
        // 如果当前层还没赋值，那么直接赋值 [root.val]
        // 否则 push root.val
        if (!nodes[level]) {
            nodes[level] = [root.val]
        } else {
            nodes[level].push(root.val)
        }
        // 递归左子树
        helper(root.left, level + 1)
        // 递归右子树
        helper(root.right, level + 1)
    }
    // 节点值保存到这个数组（将来是二维）
    let nodes = []
    // 递归
    helper(root, 0)
    // 求已保存好的每层节点的平均值
    return nodes.map((node) => {
        return node.reduce((prev, curr) => prev + curr) / node.length
    })
};

BFS

使用BFS（广度优先遍历），在遍历的过程中，将每层的节点值保存在队列中，然后将所有值出栈并相加。除以当前层的队列的长度就是这一层的平均值。将其放入结果中。重复上述步骤，直到遍历完整棵二叉树，返回最后的结果

var averageOfLevels = function(root) {
    if(!root){
        return []
    }
    const res = []
    const queue = []

    queue.push(root)
    
    while(queue.length){
        const len = queue.length
        let sum = 0
        for(let i = 0; i < len; i++){
            const cur = queue.shift()
            sum += cur.val
            if(cur.left){
                queue.push(cur.left)
            }
            if(cur.right){
                queue.push(cur.right)
            }
        }
        res.push(sum / len)
    }
    return res
};

199. 二叉树的右视图​

199. 二叉树的右视图

  1. 层次遍历二叉树；
  2. 将每一层的最后一个节点值保存到结果数组
var rightSideView = function(root) {
    //用队列，获取队列每一层最后一个节点
    if(!root) return [];
    let res = []
    let que = []
    que.push(root)
    while(que.length>0){
        let len = que.length;
        for(let i=0;i<len;i++){
            let q = que.shift();
            if(q.left){que.push(q.left)}
            if(q.right){que.push(q.right)}
            if(i==len-1){
                res.push(q.val)
            }
        }
    }
    return res;
};

递归实现

// DFS的实现：
var rightSideView = function(root) {
    if(!root) return []
    let res = []
    dfs(root, 0, res)
    return res
};

function dfs(root, level, res){
    if(root){
        if(res.length === level){
            res.push(root.val)
        }

        dfs(root.right, level+1, res)
        dfs(root.left, level+1, res)
    }
}

// BFS的实现：
var rightSideView = function(root) {
    if(!root) return []
    let res = []
    let queue = [root]
    while(queue.length > 0){
        let len = queue.length

        while(len){
            let node = queue.shift()
            if(len === 1){
                res.push(node.val)
            }
            if(node.left){
                queue.push(node.left)
            }
            if(node.right){
                queue.push(node.right)
            }
            len--
        }
    }
    return res
};

左视图

  1. 层次遍历二叉树；
  2. 将每一层的第一个节点值保存到结果数组；
var rightSideView = function(root) {
    //用队列，获取队列每一层最后一个节点
    if(!root) return [];
    let res = []
    let que = []
    que.push(root)
    while(que.length>0){
        let len = que.length;
        for(let i=0;i<len;i++){
            let q = que.shift();
            if(q.left){que.push(q.left)}
            if(q.right){que.push(q.right)}
            if(i==0){ //只需将此处改为：判断是否为当前层的第一个节点
                res.push(q.val)
            }
        }
    }
    return res;
};

404. 左叶子之和​

404. 左叶子之和

DFS

判断该当前节点是否拥有左子树 判断该左子树是否是叶子节点 是的话返回叶子节点的值 递归以上步骤

var sumOfLeftLeaves = function(root) {

    if(!root) return 0
    let val = 0;
    if(root.left&&!root.left.left&&!root.left.right){
        val = root.left.val
    }
    return val+ sumOfLeftLeaves(root.left)+sumOfLeftLeaves(root.right)
};

BFS 维护一个队列去遍历节点。 首先判断root是否存在，再把它入列。 让节点出列，出列就会把它们的左右子节点入列，不同的是，左子节点如果是左叶子节点，则它的节点值要累加给sum。 当队列为空，就遍历完所有节点，sum也累加好了。

const sumOfLeftLeaves = (root) => {
  if (root == null) return 0;
  let sum = 0;
  const queue = [];
  queue.push(root);

  while (queue.length) {
    const cur = queue.shift();
    if (cur.left) {
      if (cur.left.left == null && cur.left.right == null) {
        sum += cur.left.val;
      } else {
        queue.push(cur.left);
      }
    }
    if (cur.right) {
      queue.push(cur.right);
    }
  }
  return sum;
};

508. 出现次数最多的子树元素和​

508. 出现次数最多的子树元素和

DFS

准备几个全局变量： mxOcc: 记录出现元素最多的次数。即“maximum occurrence"。 mp：哈希表，用于维护每一个节点元素和出现的次数。 ans：用于记录答案数组。

对于每一个节点，我们首先递归查询其左子树的和，然后再递归查询其右子树的和，加上这个当前节点本身的值，那么就为该节点的元素和。 即 cur = dfs(root.left) + dfs(root.right) + root.val。

再计算完当前节点的元素和cur后，将mp中这个元素出现的次数加1。 即 mp[cur] += 1

将该元素和出现的次数与mxOcc做比较。 如果mp[cur] > mxOcc。那么则说明当前元素和的个数是最多的。于是将mxOcc跟新为当前元素和的数量，即mxOcc = mp[cur]，然后重新记录答案数组。ans = [cur] 如果mp[cur] == mxOcc。那么则说明当前元素和的个数刚好达到了最多的出现次数，直接将其元素和加入到答案数组中。ans.append(cur)

返回当前元素和。所有递归完成后直接返回答案数组即可。

var findFrequentTreeSum = function(root) {
    let mxOcc = 0;
    const mp = new Map();
    let ans = [];

    const dfs = (root) => {
        if(!root) return 0;
        const cur = root.val + dfs(root.left) + dfs(root.right);
        mp.set(cur, (mp.get(cur) || 0) + 1);
        if(mp.get(cur) > mxOcc) {
            mxOcc = mp.get(cur);
            ans = [cur];
        } else if(mp.get(cur) == mxOcc) {
            ans.push(cur);
        }
        return cur;
    }
    dfs(root);
    return ans;
};

记录每个子树的子树合集，通过最大子树和数筛选出

var findFrequentTreeSum = function(root) {
    let result = {}

    let maxCount = 0

    function dfs(p){
        if(!p){
            return 0
        }
        let leftValue = dfs(p.left)
        let rightValue = dfs(p.right)

        let total = p.val + leftValue+rightValue

        if(total in result){
            result[total]++
        }else{
            result[total] = 1
        }
        if(result[total]>maxCount){
            maxCount = result[total]
        }
        return total
    }

    dfs(root)

    let arr = Object.keys(result).reduce((arr,key)=>{
        let val = result[key]
        if(val === maxCount){
            arr.push(key)
        }

        return arr;
    },[])
    return arr
};

662. 二叉树最大宽度​

662. 二叉树最大宽度

给你一棵二叉树的根节点 root ，返回树的 最大宽度 。

树的 最大宽度 是所有层中最大的 宽度 。

0n 1n是js中用于显示大数字的定义，普通的数字超过一定数值会丢失精度，这种方式是专门做大数字的运算用的，要创建BigInt，只需要在数字末尾追加n即可

DFS

var widthOfBinaryTree = function(root) {
  let maxWidth = 1n
  let map = new Map()

  function dfsFn(node, level, pos) {
    if (!map.has(level)) {
      map.set(level, pos)
    } else {
      let curWidth = pos - map.get(level) + 1n
      if (curWidth > maxWidth) {
        maxWidth = curWidth
      }
    }
    node.left && dfsFn(node.left, level + 1, 2n * pos)
    node.right && dfsFn(node.right, level + 1, 2n * pos + 1n)
    return maxWidth
  }

  return root ? dfsFn(root, 1, 1n) : 0n
};

BFS

var widthOfBinaryTree = function(root) {
  let maxWidth = 0n
  // 先进先出
  let queue = []
  if (root) {
    queue.push([root, 1n])
  }
  while (queue.length) {
    let len = queue.length
    let positionArr = []

    for (let i = 0; i < len; i++) {
      // 处理当层
      let node = queue.shift()
      positionArr.push(node[1])
      // 遍历出下层
      if (node[0].left) {
        queue.push([node[0].left, 2n * node[1]])
      }
      if (node[0].right) {
        queue.push([node[0].right, 2n * node[1] + 1n])
      }
    }
    let start = positionArr[0]
    let end = positionArr.pop()
    let result = end - start + 1n
    if (result > maxWidth) {
      maxWidth = result
    }
  }
  return maxWidth
};

104. 二叉树的最大深度​

104. 二叉树的最大深度

var maxDepth = function (root) {
    //使用递归的方法 递归三部曲
    //1. 确定递归函数的参数和返回值
    const getdepth = function (node) {
        //2. 确定终止条件
        if (node === null) {
            return 0;
            
        }
        //3. 确定单层逻辑
        let leftdepth = getdepth(node.left);
        let rightdepth = getdepth(node.right);
        let depth = 1 + Math.max(leftdepth, rightdepth);
        return depth;

    }
    return getdepth(root);

};

111. 二叉树的最小深度​

111. 二叉树的最小深度

DFS

const minDepth = (root) => {
    if (root == null) {            // 递归到null节点，返回高度0
        return 0;
    }
    if (root.left && root.right) { // 左右子树都存在，当前节点的高度1+左右子树递归结果的较小值
        return 1 + Math.min(minDepth(root.left), minDepth(root.right));
    } else if (root.left) {        // 左子树存在，右子树不存在
        return 1 + minDepth(root.left);
    } else if (root.right) {       // 右子树存在，左子树不存在
        return 1 + minDepth(root.right);
    } else {                       // 左右子树都不存在，光是当前节点的高度1
        return 1;
    }
};

const minDepth = (root) => {
    if (root == null) {
        return 0;
    }
    const left = minDepth(root.left);
    const right = minDepth(root.right);

    if (left > 0 && right > 0) {
        return 1 + Math.min(left, right);
    } else if (left > 0) {
        return 1 + left;
    } else if (right > 0) {
        return 1 + right;
    } else {
        return 1;
    }
};
const minDepth = (root) => {
    if (root == null) return 0;

    let depth = 1;  // 当前子树的深度，有1保底 (根节点高度)

    if (root.left && root.right) { // 左右子树都存在
        depth += Math.min(minDepth(root.left), minDepth(root.right));
    } else if (root.left) {
        depth += minDepth(root.left);
    } else if (root.right) {
        depth += minDepth(root.right);
    } else {                    // 左右子树都不存在
        depth += 0;
    }
    return depth; // 返回整棵树的计算结果
};
const minDepth = (root) => {
    if (root == null) {
        return 0;
    }
    let depth = Infinity; // 当前子树的深度

    if (root.left) { // 左子树存在，用1+左子树的最小深度去刷新depth
        depth = Math.min(depth, 1 + minDepth(root.left));
    }
    if (root.right) { // 由子树存在，用1+右子树的最小深度去刷新depth
        depth = Math.min(depth, 1 + minDepth(root.right));
    }
    if (root.left == null && root.right == null) { // 都不存在
        depth = 1;   
    }
    return depth;
};

BFS

一层层遍历，一旦发现当前层的某个节点没有子节点，说明当前处在最小深度。

const minDepth = (root) => {
    if (root == null) return 0;

    const queue = [root]; // 根节点入列
    let depth = 1;        // 当前层的深度

    while (queue.length) { // 直到清空队列
        const levelSize = queue.length; // 当前层的节点个数
        for (let i = 0; i < levelSize; i++) { // 遍历 逐个出列
            const cur = queue.shift();  // 出列
            if (cur.left == null && cur.right == null) { // 如果没有孩子，直接返回所在层数
                return depth;
            }
            if (cur.left) queue.push(cur.left); // 有孩子，让孩子入列
            if (cur.right) queue.push(cur.right);
        }
        depth++; // 肯定有下一层，如果没有早就return了
    }
};

513. 找树左下角的值​

513. 找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

DFS

二叉树递归框架代码是先递归左子树，后递归右子树，所以到最大深度时第一次遇到的节点就是左下角的节点。

var findBottomLeftValue = function(root) {

  let curMaxDepth = -1, curVal = 0

  var dfs = function(root, curDepth){
    if(!root) return null;
    if(curDepth > curMaxDepth){
      curMaxDepth = curDepth
      curVal = root.val
    }

    dfs(root.left, curDepth+1)
    dfs(root.right, curDepth+1)
  }

  dfs(root, 0)
  return curVal
};

var findBottomLeftValue = function (root) {
  // 记录二叉树的最大深度
  let maxDepth = 0;
  // 记录 dfs 递归遍历到的深度
  let depth = 0;
  let res = null;
  const dfs = (root) => {
    if (root == null) return null;
    // 前序遍历位置
    depth++;
    if (depth > maxDepth) {
      // 到最大深度时第一次遇到的节点就是左下角的节点
      maxDepth = depth;
      res = root;
    }
    dfs(root.left);
    dfs(root.right);
    depth--;
  };
  dfs(root);
  return res.val;
};

BFS

var findBottomLeftValue = function(root) {
  if(!root) return null;
  const queue = [root]
  let mostLeft = null;
  while(queue.length > 0){
    let curLevelSize = queue.length
//因为是层序遍历，所以每次层的queue的第一个必然是最左边的节点
    mostLeft = queue[0]
    for(let i = 0; i < curLevelSize; i++){
      const curNode = queue.shift();

      curNode.left && queue.push(curNode.left)
      curNode.right&& queue.push(curNode.right)
    }
  }

  return mostLeft.val
};

222. 完全二叉树的节点个数​

222. 完全二叉树的节点个数

DFS

var countNodes=function(root){
    if(!root) return 0
    let count=1
    const dfs=(node)=>{
        if(node.left){
            count++
            dfs(node.left)
        }
        if(node.right){
            count++;
            dfs(node.right)
        }
    }
    dfs(root)
    return count
}

简化DFS

function countNodes(root) {
    const dfs = (root, step) => {
        if (!root) return 0;
        const left = dfs(root.left, step + 1);
        const right = dfs(root.right, step + 1);
        return left + right + 1;
    }
    return dfs(root, 0);
};

BFS

const countNodes=function(root){
   if(!root) return 0
     let queue=[root]
     let count=1
     while(queue.length){
        let node=queue.pop()
        if(node.left){
            queue.push(node.left)
            count++
        }
        if(node.right){
            queue.push(node.right)
            count++
        }

     }
     return count
}

654. 最大二叉树​

654. 最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。 递归地在最大值 左边 的 子数组前缀上 构建左子树。 递归地在最大值 右边 的 子数组后缀上 构建右子树。 返回 nums 构建的 最大二叉树 。

DFS

递归 找出最大值 分出左-最大值-右三个部分

var constructMaximumBinaryTree = function(nums) {
    if (!nums.length) {
        return null
    }
    
    let max = nums.reduce((init, curr) => {
        init = init < curr ? curr : init
        return init
    }, 0)
    
    let maxIdx = nums.indexOf(max)
    let left = nums.slice(0, maxIdx)
    let right = nums.slice(maxIdx + 1)
    
    let root = new TreeNode(max)
    root.left = constructMaximumBinaryTree(left)
    root.right = constructMaximumBinaryTree(right)
    
    return root   
}

110. 平衡二叉树​

自顶向下（暴力法）​

解题思路： 自顶向下的比较每个节点的左右子树的最大高度差，如果二叉树中每个节点的左右子树最大高度差小于等于 1 ，即每个子树都平衡时，此时二叉树才是平衡二叉树

var isBalanced = function (root) {
  if(!root) return true
  return Math.abs(depth(root.left) - depth(root.right)) <= 1
        && isBalanced(root.left)
        && isBalanced(root.right)
}
var depth = function (node) {
    if(!node) return -1
    return 1 + Math.max(depth(node.left), depth(node.right))
}

复杂度分析：

时间复杂度：O(nlogn)，计算 depth 存在大量冗余操作 空间复杂度：O(n)

自底向上（优化）​

解题思路： 利用后续遍历二叉树（左右根），从底至顶返回子树最大高度，判定每个子树是不是平衡树 ，如果平衡，则使用它们的高度判断父节点是否平衡，并计算父节点的高度，如果不平衡，返回 -1 。

遍历比较二叉树每个节点 的左右子树深度：

比较左右子树的深度，若差值大于 1 则返回一个标记 -1 ，表示当前子树不平衡 左右子树有一个不是平衡的，或左右子树差值大于 1 ，则二叉树不平衡 若左右子树平衡，返回当前树的深度（左右子树的深度最大值 +1 ） 代码实现：

var isBalanced = function (root) {
    return balanced(root) !== -1
};
var balanced = function (node) {
    if (!node) return 0
    const left = balanced(node.left)
    const right = balanced(node.right)
    if (left === -1 || right === -1 || Math.abs(left - right) > 1) {
        return -1
    }
    return Math.max(left, right) + 1
}

复杂度分析：

时间复杂度：O(n) 空间复杂度：O(n)

226. 翻转二叉树​

226. 翻转二叉树

function invertTree(root){
    if(!root) return null
    const queue=[root]
    while(queue.length){
        const node=queue.shift()

        const temp=node.right;
        node.right=node.left;
        node.left=temp;
        
        node.left&&queue.push(node.left)
        node.right&&queue.push(node.right)

    }
    return root
}

617. 合并二叉树​

617. 合并二叉树

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

DFS

直接在t1上修改

进行值相加, 然后就是左跟左, 右跟右合, 递归下去, 注意下递归终止条件就行了

var mergeTrees = function(t1, t2) {
    if(!t1 && t2){
        return t2
    }
    if(t1 && !t2 || !t1 && !t2){
        return t1
    }

    t1.val += t2.val
    t1.left = mergeTrees(t1.left, t2.left)
    t1.right = mergeTrees(t1.right, t2.right)
    return t1
};

BFS

整一个队列先把两个节点都放入队列, 然后取出节点累加, 再看它们的左右节点,

如果都存在, 就继续放入队列中

如果1不存在但2存在, 就把2的值赋给1, 因为最后是返回t1的, 我们都把值合并到t1上

var mergeTrees = function(t1, t2) {
  if( !t1 || !t2 ) return t1 || t2
  let queue = [ [t1, t2] ]
  while( queue.length ) {
    let [ h1, h2 ] = queue.shift()
    let { left: l1, right: r1 } = h1
    let { left: l2, right: r2 } = h2
    // 两个都存在则值累计
    if( h1 && h2 ) h1.val += h2.val
    if( l1 && l2 ) queue.push( [l1, l2] )
    if( r1 && r2 ) queue.push( [r1, r2] )
    // 1不存在 且 2存在,  则把 2的值赋给 1
    if( !l1 && l2 ) h1.left = h2.left
    if( !r1 && r2 ) h1.right = h2.right
  }
  return t1
};

114. 二叉树展开为链表​

114. 二叉树展开为链表

给你二叉树的根结点 root ，请你将它展开为一个单链表：

展开后的单链表应该同样使用 TreeNode ，其中 right 子指针指向链表中下一个结点，而左子指针始终为 null 。 展开后的单链表应该与二叉树 先序遍历 顺序相同。

将树的right树替换为left树 将left树的最右节点的 right 指向当前树的right树 （因为left树经过处理后后变成了只有right节点的链表 需要链表的尾部指向right树） 递归此操作

var flatten = function(root) {
    // 递归终止条件
    if (root === null) return null;
    
    // 分别递归左右节点
    const left = root.left;
    const right = root.right;
    flatten(left)
    flatten(right);
    
    // 将树的right节点替换为left节点
    root.right = root.left;
    root.left = null;

    // 循环 找到最右的节点
    while (root.right) root = root.right;
    // 最右的节点 指向 right 节点
    root.right = right;
};

右子树转成的单链表，只要获取它的头结点，等左子树生成的链表生成好，接到它的尾节点 左子树生成的单链表，处理稍微复杂一点 要获取它的头结点，它要接到根节点的right 要获取它的尾节点，通过一直找右节点，找到尾节点，供连接 左子树生成的链表两端都接好后，root.left 要置为 null，不然 root 还拖着个左子树

const flatten = (root) => {
  const helper = (root) => {       // 将当前子树转成一个单链表
    if (root == null) return null; // 遍历到null节点 返回null节点
    if (root.right) {              // 先生成右子树的单链表
      helper(root.right);
    }
    if (root.left) {               // 如果有左子树，生成单链表然后搬运过去
      const leftFirst = helper(root.left); // 生成单链表，并获取头结点
      let leftLast = leftFirst;    // leftEnd是单链表的尾节点
      while (leftLast.right) {     // 一直找右节点，获取到单链表的尾节点
        leftLast = leftLast.right;
      }
      leftLast.right = root.right; // 尾节点后面接左子树展平后的单链表
      root.right = leftFirst;      // 根节点的right改成leftFirst
      root.left = null;            // root.left置为null
    }
    return root; // 返回出当前子树转成的单链表
  };
  helper(root);  // 原地修改，不用返回
};

105. 从前序与中序遍历序列构造二叉树​

105. 从前序与中序遍历序列构造二叉树

前序遍历：根-左-右 中序遍历：左-根-右 先用前序遍历找根节点，在用根节点去中序遍历确定左右子树 递归 注意退出递归条件

var buildTree = function(preorder, inorder) {
  // 退出递归条件
  if (!inorder.length) {
    return null
  }
  let temp = preorder[0]  // 根节点
  let mid = inorder.indexOf(temp) // 根节点在中序遍历中的下标
  let root = new TreeNode(temp)
  // 根在中序的mid，那左子树个数就有mid个
  // 前序里截取从第1个到第mid+1个是左子树，中序里第0个到第mid个是左子树
  root.left = buildTree(preorder.slice(1, mid + 1), inorder.slice(0, mid))
  // 前序里截取从第mid+1个到最后是右子树，中序里第mid个到最后是右子树
  root.right = buildTree(preorder.slice(mid + 1), inorder.slice(mid + 1))
  return root
};

优化

字符串截取存在性能消耗，没必要每次都切割。用两个指针表示即可。递归函数传指针。

  • indexOf 的使用导致每次递归都花 O(n) 的时间定位根节点的位置，不理想。
  • 提前把 inorder 的元素和索引存到哈希表中，用空间换取时间。
const buildTree = (preorder, inorder) => {
  const map = new Map();
  for (let i = 0; i < inorder.length; i++) {
    map.set(inorder[i], i);
  }
  const helper = (p_start, p_end, i_start, i_end) => {
    if (p_start > p_end) return null;
    let rootVal = preorder[p_start];    // 根节点的值
    let root = new TreeNode(rootVal);   // 根节点
    let mid = map.get(rootVal);         // 根节点在inorder的位置
    let leftNum = mid - i_start;        // 左子树的节点数
    root.left = helper(p_start + 1, p_start + leftNum, i_start, mid - 1);
    root.right = helper(p_start + leftNum + 1, p_end, mid + 1, i_end);
    return root;
  };
  return helper(0, preorder.length - 1, 0, inorder.length - 1);
};

106. 从中序与后序遍历序列构造二叉树​

106. 从中序与后序遍历序列构造二叉树

中序遍历：左-根-右

后序遍历：左-右-根

先用后序遍历找根节点，在用根节点去中序遍历确定左右子树 递归 注意退出递归条件

var buildTree=function (inorder,postorder){
    if(!inorder.length) return null;
    const rootVal=postorder.pop()
    let rootIndex=inorder.indexOf(rootVal)
    const root=new TreeNode(rootVal)
    root.left = buildTree(inorder.slice(0, rootIndex), postorder.slice(0, rootIndex))
    root.right = buildTree(inorder.slice(rootIndex + 1), postorder.slice(rootIndex))
    return root;
}

优化

const buildTree = (inorder, postorder) => {
  const map = {};
  for (let i = 0; i < inorder.length; i++) { // 将节点值在inorder数组中的位置提前存入map
    map[inorder[i]] = i;
  }
  // 根据iStart到iEnd的inorder数组，和从pStart到pEnd的postorder数组构建当前子树
  const helper = (iStart, iEnd, pStart, pEnd) => { 
    if (pStart > pEnd || iStart > iEnd) { // 指针交错了，返回null节点
      return null;
    }
    const rootVal = postorder[pEnd]; // 获取当前要构建的根节点的值
    const mid = map[rootVal];        // 获取到它在inorder数组中的位置
    const leftNodeNum = mid - iStart; // 获取左子树的节点个数

    const root = new TreeNode(rootVal); // 创建节点
    root.left = helper(iStart, mid - 1, pStart, pStart + leftNodeNum - 1); // 用递归构建左子树
    root.right = helper(mid + 1, iEnd, pStart + leftNodeNum, pEnd - 1); // 用递归构建右子树

    return root; // 返回当前构建好的子树
  };

  return helper(0, inorder.length - 1, 0, postorder.length - 1); // 递归的入口
};

889. 根据前序和后序遍历构造二叉树​

889. 根据前序和后序遍历构造二叉树

中序遍历：左-根-右

后序遍历：左-右-根

var constructFromPrePost = function(pre, post) {
    if(pre.length == 0) return null;
    let tmp = pre[0];
    let index = post.indexOf(pre[1]);
    let root = new TreeNode(tmp);
    root.left = constructFromPrePost(pre.slice(1,index+2),post.slice(0,index+1));
    root.right = constructFromPrePost(pre.slice(index+2),post.slice(index+1,post.length-1));
    return root;
};

116. 填充每个节点的下一个右侧节点指针​

116. 填充每个节点的下一个右侧节点指针

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

DFS

const connect = (root) => {
  if (root == null) {
    return root;
  }
  const dfs = (root) => {
    if (root.left == null && root.right == null) {
      return;
    }
    root.left.next = root.right;
    if (root.next) {
      root.right.next = root.next.left;
    }
    dfs(root.left);
    dfs(root.right);
  };
  dfs(root);
  return root;
};

BFS

使用队列层层遍历，同一层的节点的 next 指针指向它后面的兄弟节点，每一层最后的节点 的 next 指针指到 null

var connect = function(root) {
  if (!root) return root;
  let queue = [root];
  
  while (queue.length > 0) {
    let size = queue.length;
    while (size > 0) {
      size--;
      let offer = queue.shift();
      
      if (offer) {
        if (size === 0) {
          offer.next = null;
        } else {
          offer.next = queue[0];
        }
      }
      if (offer && offer.left) queue.push( offer.left );
      if (offer && offer.right) queue.push( offer.right );
    }
  }
  
  return root;
};

117. 填充每个节点的下一个右侧节点指针 II​

117. 填充每个节点的下一个右侧节点指针 II

填充它的每个 next 指针，让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点，则将 next 指针设置为 NULL。

初始状态下，所有 next 指针都被设置为 NULL。

进阶：

  • 你只能使用常量级额外空间。
  • 使用递归解题也符合要求，本题中递归程序占用的栈空间不算做额外的空间复杂度。

对于这道题目，我们可以对树进行层序遍历，树的层序遍历是基于广度优先遍历的，按照层的顺序进行遍历，我们需要舒适话一个队列queue，这个队列中保存着当前层的节点。

当队列不为空的时候就记录当前队列的的长度len，当遍历这一层的时候，修改这一层节点的 next 指针，这样就可以把每一层都组织成链表。

/**
 * // Definition for a Node.
 * function Node(val, left, right, next) {
 *    this.val = val === undefined ? null : val;
 *    this.left = left === undefined ? null : left;
 *    this.right = right === undefined ? null : right;
 *    this.next = next === undefined ? null : next;
 * };
 */

/**
 * @param {Node} root
 * @return {Node}
 */
var connect = function(root) {
    if (!root) {
        return null;
    }
    const queue = [root];
    while (queue.length) {
        const len = queue.length;
        let last = null;
        for (let i = 1; i <= len; ++i) {
            let node = queue.shift();
            if (node.left) {
                queue.push(node.left);
            }
            if (node.right) {
                queue.push(node.right);
            }
            if (i !== 1) {
                last.next = node;
            }
            last = node;
        }
    }
    return root;
};

不使用额外空间的优化

使用BFS需要O(n)的空间复杂度，如何不需要额外的空间复杂度呢 在上一层为下一层建立 next 指针 当遍历到某层节点时，该层节点的 next 指针已经建立，这样就不需要队列了，只要知道下一层的最左边的节点，就可以从该节点开始，像遍历链表一样遍历该层的所有节点 时间复杂度：O(N)。我们需要遍历这棵树上所有的节点，所以时间复杂度为 O(N) 空间复杂度：O(1)

var connect = function (root) {
  // 上一个节点
  let last,
    // 下一层从左至右第一个节点，也就是下一层中最左边节点
    nextStart;
  const handle = (p) => {
    // 上一个节点的next指针指向当前节点
    if (last !== null) last.next = p;
    // 如果下一层中最左边节点为空 则将下一个节点指向当前节点，先记录起来方便下一层循环使用
    if (nextStart === null) nextStart = p;
    // 向前走一步  保留当前节点以便下一轮使用
    last = p;
  };
  if (root === null) return null;

  let start = root;
  while (start != null) {
    last = null;
    nextStart = null;
    for (let p = start; p !== null; p = p.next) {
      // 先处理左节点再处理右节点 处理完之后下一层的next指针就已经建立好了
      if (p.left) handle(p.left);
      if (p.right) handle(p.right);
    }
    // 进入下一层
    start = nextStart;
  }
  return root;
};

297. 二叉树的序列化与反序列化​

297. 二叉树的序列化与反序列化

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

BFS

思路：广度优先遍历节点，不断子节点不断入队，按照根左右的顺序序列化和反序列化 复杂度：时间复杂度O(n)，每个节点访问一次，n是树的节点个数。空间复杂度O(n)，队列的空间

const serialize = (root) => {
    const queue = [root];
    let res = [];
    while (queue.length) {
        const node = queue.shift(); //出队
        if (node) {                 //node存在 推入根左右
            res.push(node.val);
            queue.push(node.left);
            queue.push(node.right);
        } else {                    //如果不存在 推入‘x’
            res.push('X');
        }
    }
    return res.join(',');  //数组转成字符串
}

const deserialize = (data) => {
    if (data == 'X') return null;

    const list = data.split(',');  //字符串转数组

    const root = new TreeNode(list[0]); //从队首开始构建
    const queue = [root];          //根节点加入队列
    let cursor = 1;                //遍历到了第几个节点

    while (cursor < list.length) { //当队列没遍历完时
        const node = queue.shift();  //出队

        const leftVal = list[cursor];      //左节点的值
        const rightVal = list[cursor + 1]; //右节点的值

        if (leftVal != 'X') {              //不是空节点
            const leftNode = new TreeNode(leftVal); //构建左节点
            node.left = leftNode;                   //左节点挂在父节点的left下
            queue.push(leftNode);                   //自己入列 构建以自己为根的子树
        }
        if (rightVal != 'X') {
            const rightNode = new TreeNode(rightVal);
            node.right = rightNode;
            queue.push(rightNode);
        }
        cursor += 2; //构建的节点数+2
    }
    return root;  //返回根
};

DFS

思路：深度优先遍历，按根,左,右 返回字符串，方便反序列化的时候从根节点开始构建，递归左右子树，直到遇见了null节点。 复杂度：时间复杂度O(n)，每个节点访问一次，n是树的节点个数。空间复杂度O(n)，最坏情况下递归深度是n

const serialize = (root) => {
    if (root == null) {                  //遇到null 返回‘X’进行标示
        return 'X';
    }
    const left = serialize(root.left);   //序列化左子树
    const right = serialize(root.right); //序列化右子树
    return root.val + ',' + left + ',' + right; //按根,左,右 返回字符串
};

const deserialize = (data) => {
    const list = data.split(',');   //字符串转数组

    const buildTree = (list) => {   //构建树
        const rootVal = list.shift(); //第一个元素
        if (rootVal == "X") {         //如果是X，返回null
            return null;
        }
        const root = new TreeNode(rootVal); //如果不是X就创建节点
        root.left = buildTree(list);        //构建左子树
        root.right = buildTree(list);       //构建右子树
        return root;                        //返回构建的节点
    };

    return buildTree(list);
};

98. 验证二叉搜索树​

98. 验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

节点的左子树只包含 小于 当前节点的数。 节点的右子树只包含 大于 当前节点的数。 所有左子树和右子树自身必须也是二叉搜索树。

中序遍历​

中序遍历，如果小于右子树或者根节点，就是false，想一个节点就行

var isValidBST = function(root) {
    if (root === null) return true;
    let node = root,
        stack = [];
    let pre = -Infinity;
    while (stack.length > 0 || node !== null) {
        if (node) {
            stack.push(node);
            node = node.left;
        } else {
            node = stack.pop();
            if (pre >= node.val) return false;
            pre = node.val;
            node = node.right;
        }
    }
    return true;
};

递归​

递归要保证每一个节点的左子树的所有值不能大于当前值，右子树的所有值不能大于当前值。 因此要设置一个上边界和下边界。

var isValidBST = function(root) {
    return help(root, null, null)
};

function help(node, low, high) {
    if (node === null) return true;
    let val = node.val;
    
    // 不能小于下边界
    if (low !== null && val <= low) return false;
    // 不能大于上边界
    if (high !== null && val >= high) return false;
    
    // 左子树的上边界是当前节点值
    if (!help(node.left, low, val)) return false;
    // 右子树的下边界是当前节点值
    if (!help(node.right, val, high)) return false;
    return true
}

递归转成迭代​

var isValidBST = function(root) {
    let stack = [], // 存储所有的节点
        lowS = [], // 存储对应节点的下边界
        highS = []; // 存储对应节点的上边界
    
    function help(node, low, high) {
        stack.push(node);
        lowS.push(low);
        highS.push(high);
    }
    
    let low = null, high = null, val, node;
    help(root, low, high);
    
    while (stack.length > 0) {
        node = stack.pop();
        low = lowS.pop();
        high = highS.pop();
        
        if (node === null) continue;
        val = node.val;
        if (low !== null && val <= low) return false;
        if (high !== null && val >= high) return false;
        help(node.left, low, val);
        help(node.right, val, high);
    }
    return true;
};

230. 二叉搜索树中第K小的元素​

230. 二叉搜索树中第K小的元素

递归：BST的中序遍历相当于是升序排列，用一个数组承接遍历的值，最终返回第k-1个元素（数组下标从0开始）

var kthSmallest = function(root, k) {
    let nums=[];
    function dfs(root){
      if(!root) return;
      dfs(root.left);
      nums.push(root.val);
      dfs(root.right);
    }
    dfs(root);
    return nums[k-1];
};

使用栈进行优化

var kthSmallest = function(root, k) {
  const stack = [];

  while(true) {
    while(root) {
      stack.push(root);
      root = root.left;
    }
    root = stack.pop();
    k--;
    if(k === 0) {
      return root.val;
    }
    root = root.right;
  }
};

剑指 Offer 54. 二叉搜索树的第k大节点​

剑指 Offer 54. 二叉搜索树的第k大节点

采用中序遍历，将二叉搜索树的节点值以升序放在数组中； 然后采用数组的逆序方法，返回第k-1个数值

var kthLargest = function(root, k) {
//   中序遍历
    var roots = [];
    //  中序遍历的接口
    var inOrderTraverse = function(node) {
        if(node !== null){
           inOrderTraverse(node.left);
           roots.push(node.val);
           inOrderTraverse(node.right);
        }
    }
    inOrderTraverse(root);
    roots.reverse();
    return roots[--k];
};

530. 二叉搜索树的最小绝对差​

530. 二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。

差值是一个正数，其数值等于两值之差的绝对值。

中序遍历将二叉搜索树转换为升序数组，然后定义一个最小值，遍历数组即可。时间复杂度O(n)，空间复杂度O(n)

var getMinimumDifference = function(root) {
    let arr = [];
    function inorder(node){
        if (node){
            inorder(node.left);
            arr.push(node.val);
            inorder(node.right);
        }
        return arr;
    }
    inorder(root);
    let minDiffValue = Number.MAX_SAFE_INTEGER;
    for (let i = 0; i < arr.length - 1; i++){
        minDiffValue = Math.min(minDiffValue, arr[i + 1] - arr[i]);
    }
    return minDiffValue;
};

DFS

var getMinimumDifference = function (root) {
  let prev = null;
  let res = Number.MAX_SAFE_INTEGER;
  let dfs = (root) => {
    if (root == null) return res;
    dfs(root.left);
    // 中序遍历位置
    if (prev != null) {
      res = Math.min(res, root.val - prev.val);
    }
    prev = root;
    dfs(root.right);
  };
  dfs(root);
  return res;
};

501. 二叉搜索树中的众数​

501. 二叉搜索树中的众数

运用对象不能有相同的键的属性 遍历树的每个节点，判断对象中是否有该 节点val的键，有则值加一，没有则对象添加一个键为节点的val值为1

var findMode = function(root) {
    let obj={}
    let getMax=function(node){
        if(!node) return;
        if(obj.hasOwnProperty(node.val)){
            obj[node.val]++
        }else{
            obj[node.val]=1
        }
        getMax(node.left)
        getMax(node.right)
    }
    getMax(root)
    let max=0;
    let nums=[]
    for(let item in obj){
        if(obj[item]>max){
            max=obj[item]
        }
    }
    for(let item in obj){
        if(obj[item]===max){
            nums.push(item)
        }
    }
    return nums
};

DFS

var findMode = function(root) {
    let pre
    let preNum
    let max = 0
    let result = []
    function DFS(root){
        if(root==null) return
        root.left && DFS(root.left)
        if(root.val == pre) {
            preNum++
        } else {
            pre = root.val
            preNum = 1
        }
        if(preNum>max) {
            result = [root.val]
            max = preNum
        } else if(preNum==max){
            result.push(root.val)
        }
        root.right && DFS(root.right)
    }
    DFS(root)
    return result
};

108. 将有序数组转换为二叉搜索树​

108. 将有序数组转换为二叉搜索树

给你一个整数数组 nums ，其中元素已经按 升序 排列，请你将其转换为一棵 高度平衡 二叉搜索树。

高度平衡 二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

var sortedArrayToBST = function (nums) {
    if (!nums.length) {
        return null
    }

    // 二叉搜索树的中序遍历，就是升序列表
    // 以升序数组的中间元素作为根节点 root
    const mid = Math.floor(nums.length / 2)
    const root = new TreeNode(nums[mid])

    root.left = sortedArrayToBST(nums.slice(0, mid))
    root.right = sortedArrayToBST(nums.slice(mid + 1))

    return root
};

109. 有序链表转换二叉搜索树​

109. 有序链表转换二叉搜索树

给定一个单链表的头节点 head ，其中的元素 按升序排序 ，将其转换为高度平衡的二叉搜索树。

一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差不超过 1。

二分法

const sortedListToBST = (head) => {
    const arr = [];
    while (head) { // 将链表节点的值逐个推入数组arr
        arr.push(head.val);
        head = head.next;
    }
    // 根据索引start到end的子数组构建子树
    const buildBST = (start, end) => {
        if (start > end) return null;        // 指针交错，形成不了子序列，返回null节点
        const mid = (start + end) >>> 1;     // 求中间索引 中间元素是根节点的值
        const root = new TreeNode(arr[mid]); // 创建根节点
        root.left = buildBST(start, mid - 1); // 递归构建左子树
        root.right = buildBST(mid + 1, end);  // 递归构建右子树
        return root;                          // 返回当前子树
    };

    return buildBST(0, arr.length - 1);  // 根据整个arr数组构建
};

538. 把二叉搜索树转换为累加树​

538. 把二叉搜索树转换为累加树

给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

const convertBST=(root)=>{
    let sum=0
    let stack=[]
    let cur=root
    while(cur){   //右节点压入
        stack.push(cur)
        cur=cur.right
    }
    while(stack.length){
        cur=stack.pop()
        sum+=cur.val
        cur.val=sum
        cur=cur.left
        while(cur){
            stack.push(cur)
            cur=cur.right
        }
    }
    return root
}
// 逆向中序遍历，左中右->右中左
// 节点的值等于它自己加上它的前一个节点的值【逆向】
var convertBST = function(root) {
    if(!root) return null;
    let stack = [];
    let node = root;
    let prenode = null;
    while(node || stack.length) {
        while(node) {
            stack.push(node)
            node = node.right;
        }
        node = stack.pop();
        if(prenode) {
            node.val += prenode.val;
        }
        prenode = node;
        node = node.left;
    }
    return root;
};

700. 二叉搜索树中的搜索​

700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

迭代

var searchBST = function(root, val) {
    if (!root || val===undefined) return null;
    while(root) {
        if (root.val === val) return root;
        if (root.val > val) {
            root = root.left;
        } else {
            root = root.right
        }
    }
    return null;
};

BFS前序遍历

var searchBST = function(root, val) {
    if (!root || val===undefined) return null;
    if (root.val === val) return root;
    return root.val > val ? searchBST(root.left, val) : searchBST(root.right, val);
};

701. 二叉搜索树中的插入操作​

701. 二叉搜索树中的插入操作

给定二叉搜索树（BST）的根节点 root 和要插入树中的值 value ，将值插入二叉搜索树。 返回插入后二叉搜索树的根节点。 输入数据 保证 ，新值和原始二叉搜索树中的任意节点值都不同。

递归

找到合适的插入位置 如果目标值大于当前值，则在右子树上插入 如果目标值小于当前值，则在左子树上插入 直到找到空位置插入新节点

var insertIntoBST = function(root, val) {
    if(root == null) return new TreeNode(val)
    if (root.val < val) {
        root.right = insertIntoBST(root.right, val)
    }
    if (root.val > val) {
        root.left = insertIntoBST(root.left, val)
    }
    return root
};

迭代

var insertIntoBST = function(root, val) {
    if(root==null) return new TreeNode(val);
    var parent = root,p=root;
    while(p!=null){
        parent = p;
        p=p.val<val ? p.right:p.left;
    }
    if(parent.val<val){
        parent.right = new TreeNode(val);
    }else{
        parent.left = new TreeNode(val);
    }
    return root;
};

1382.将二叉搜索树变平衡​

1382. 将二叉搜索树变平衡

给你一棵二叉搜索树，请你返回一棵 平衡后 的二叉搜索树，新生成的树应该与原来的树有着相同的节点值。如果有多种构造方法，请你返回任意一种。

如果一棵二叉搜索树中，每个节点的两棵子树高度差不超过 1 ，我们就称这棵二叉搜索树是 平衡的 。

  1. 拿到中序遍历结果
  2. 根据中序遍历序列，构建BST，而怎样构建BST就是（根节点在数组中心，数组左侧是左子树元素，右侧是右子树元素，递归进行即可）
var balanceBST = function (root) {
  const traverse = (root) => {
    let res = [];
    if (root == null) return res;
    res.push(...traverse(root.left));
    res.push(root.val);
    res.push(...traverse(root.right));
    return res;
  };
  const build = (nums, low, high) => {
    // BST 构造函数，见 108. 将有序数组转换为二叉搜索树
    if (low > high) return null;
    let mid = low + ((high - low) >> 1);
    return new TreeNode(
      nums[mid],
      build(nums, low, mid - 1),
      build(nums, mid + 1, high)
    );
  };
  // 中序遍历获取有序数组
  let nums = traverse(root);
  // 从有序数组构建 BST(前闭后闭区间)
  return build(nums, 0, nums.length - 1);
};

669. 修剪二叉搜索树​

669. 修剪二叉搜索树

给你二叉搜索树的根节点 root ，同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。 可以证明，存在 唯一的答案 。

var trimBST = function(root, low, high) {
    const dfs = (root) => {
        if (!root) {
            return null;
        }
        if (root.val <= high && root.val >= low) {
            root.left = dfs(root.left);
            root.right = dfs(root.right);
            return root;
        } else if (root.val < low) {
            return dfs(root.right);
        } else {
            return dfs(root.left);
        }

    }
    return dfs(root)
};

450. 删除二叉搜索树中的节点​

450. 删除二叉搜索树中的节点

给定一个二叉搜索树的根节点 root 和一个值 key，删除二叉搜索树中的 key 对应的节点，并保证二叉搜索树的性质不变。返回二叉搜索树（有可能被更新）的根节点的引用。

var deleteNode = function(root, key) {
    if(!root) return null;

    // 说明需要去右子树中删除
    if(root.val < key) {
        root.right = deleteNode(root.right, key)
    } 
    // 说明需要去左子树种删除
    else if(root.val > key) {
        root.left = deleteNode(root.left, key)
    } 
    // 刚好等于要删除的值
    else {
        // 如果是叶子节点
        if(!root.left && !root.right) {
            root = null;
        }

        // 如果有右子树，则用后继节点代替当前的节点，并删除后继节点，并将删除后继节点后的结果，赋值给当前节点的右子树
        else if(root.right) {
            root.val = successor(root);
            root.right = deleteNode(root.right, root.val)
        }
        // 如果只有左子树，则用当前节点的前驱结点代替当前的节点，并删除前驱结点，并将删除前驱节点后的结果，赋值给当前节点的左子树
        else {
            root.val = predecessor(root);
            root.left = deleteNode(root.left, root.val)
        }
    }

    return root;
};

// 某个节点的后继节点
function successor(node) {
    node = node.right;
    while(node.left) {
        node = node.left
    }
    return node.val;
}

// 某个节点的前驱结点
function predecessor(node) {
    node = node.left;
    while(node.right) {
        node = node.right;
    }
    return node.val
}

235. 二叉搜索树的最近公共祖先​

235. 二叉搜索树的最近公共祖先

利用二叉搜索树的性质可以得出：对于一个节点如果为 p 和 q 的最近公共祖先，则 p 和 q 分布在该节点的两侧子树中。

var lowestCommonAncestor = function(root, p, q) {
  let ancestor = root;
  while (true) {
    if (p.val < root.val && q.val < root.val) {
      root = root.left;
    } else if (p.val > root.val && q.val > root.val) {
      root = root.right;
    } else {
      ancestor = root;
      break;
    }
  }
  return ancestor;
};

236. 二叉树的最近公共祖先​

236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）

DFS

左孩子是null，直接返回右边的孩子值，如果是null，也会返回，然后继续回溯，再向上找父节点 如果左右都有值，那当前节点就是公共祖先节点

var lowestCommonAncestor = function(root, p, q) {
    const travelTree=function(root,p,q){
            if(root===null||root===p||root===q){
                return root
            }
            let left=travelTree(root.left,p,q)
            let right =travelTree(root.right,p,q)
            if (left !== null && right !== null) {//如果在某一个节点的左右子树都能找到p和q说明这个节点就是公共祖先
                return root
            }
            if(left===null){
                return right
            }
            return left
        }
        return travelTree(root,p,q)
};

栈和队列​

20. 有效的括号​

20. 有效的括号

var isValid = function (s) {
    let m = s.length
    if (m % 2 !== 0) return false
    let map = new Map([
        ['{', '}'],
        ['(', ')'],
        ['[', ']']
    ])
    let stk = []
    for (ch of s) {
        if (map.has(ch)) {
            stk.push(ch)
            //console.log(stk);
        } else {
            if (map.get(stk[stk.length - 1]) !== ch || stk.length == 0) return false
            else stk.pop()
        }
    }
    if (stk.length == 0) return true
    else return false
};

224. 基本计算器​

224. 基本计算器

匹配到加减号 加号把符号栈最后一位赋值给sign 减号取反 每次匹配到(将当前sign压入符号栈，匹配到)出栈 匹配到数字时 一直匹配直到不是数字时，res+=当前数字*sign

var calculate = function(s) {
        let str=s.replaceAll(' ','')
        let sign=1;
        let ops=[1]
        let i=0,res=0;
        while(i<str.length){
            if(str[i]==='+'){
                sign=ops[ops.length-1]
            }else if(str[i]==='-'){
                sign=-ops[ops.length-1];
            }else if(str[i]==='('){
                ops.push(sign)
            }else if(str[i]===')'){
                ops.pop()
            }else{
                let num=''
                while(i<str.length&&!(isNaN(Number(str[i])))){
                    num+=str[i]
                    i++;
                }
                i--;
                res+=sign*Number(num)
            }
            i++
        }
            return res
            
    }

232. 用栈实现队列​

232. 用栈实现队列

请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作（push、pop、peek、empty）

/* 
使用两个栈，s1中存储的是后入队的元素，s2中存储的是先入队的元素
入队时，元素默认存储在s1。
出队时，默认从s2进行出栈操作，如果s2为空，则将s1中元素转移到s2。
如果s2有值，则队首在s2的栈顶。否则，队首在top。
由于s1的元素只有在pop时才会转移到s2，因此只有两个栈都为空时，队列才为空。


*/
var MyQueue = function() {
    this.s1=[]
    this.s2=[]
    this.top=null
};

/** 
 * @param {number} x
 * @return {void}
 */
MyQueue.prototype.push = function(x) {
        if(!this.s1.length){
            this.top=x
        }
        this.s1.push(x)
};

/**
 * @return {number}
 */
MyQueue.prototype.pop = function() {
        if(this.s2.length){
            return this.s2.pop()
        }
        while(this.s1.length){
            this.s2.push(this.s1.pop())
        }
        return this.s2.pop()
};  

/**
 * @return {number}
 */
MyQueue.prototype.peek = function() {
    // 如果s2中有元素，则栈顶即为队首
    if (this.s2.length) {
        return this.s2[this.s2.length - 1];
    }

    // s2中无元素，则此时队首在top
    return this.top;


};

/**
 * @return {boolean}
 */
MyQueue.prototype.empty = function() {
    // 由于s1的元素只有在pop时才会转移到s2，因此判空时要两个栈一起判断
    return !this.s1.length && !this.s2.length;
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * var obj = new MyQueue()
 * obj.push(x)
 * var param_2 = obj.pop()
 * var param_3 = obj.peek()
 * var param_4 = obj.empty()
 */

225. 用队列实现栈​

225. 用队列实现栈

请你仅使用两个队列实现一个后入先出（LIFO）的栈，并支持普通栈的全部四种操作（push、top、pop 和 empty）。

实现 MyStack 类：

void push(int x) 将元素 x 压入栈顶。 int pop() 移除并返回栈顶元素。 int top() 返回栈顶元素。 boolean empty() 如果栈是空的，返回 true ；否则，返回 false

使用两个队列

用两个队列que1和que2实现队列的功能，que2其实完全就是一个备份的作用，把que1最后面的元素以外的元素都备份到que2，然后弹出最后面的元素，再把其他元素从que2导回que1

225.用队列实现栈

queue.push(1);        
queue.push(2);        
queue.pop();   // 注意弹出的操作       
queue.push(3);        
queue.push(4);       
queue.pop();  // 注意弹出的操作    
queue.pop();    
queue.pop();    
queue.empty();    
var MyStack = function() {
    this.queue1 = [];
    this.queue2 = [];
};

MyStack.prototype.push = function(x) {
    this.queue1.push(x);
};

MyStack.prototype.pop = function() {
    // 减少两个队列交换的次数， 只有当queue1为空时，交换两个队列
    if(!this.queue1.length) {
        [this.queue1, this.queue2] = [this.queue2, this.queue1];
    }
    while(this.queue1.length > 1) {
        this.queue2.push(this.queue1.shift());
    }
    return this.queue1.shift();
};
MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue1.push(x);
    return x;
};
MyStack.prototype.empty = function() {
    return !this.queue1.length && !this.queue2.length;
};

使用一个队列实现


var MyStack = function() {
    this.queue = [];
};

MyStack.prototype.push = function(x) {
    this.queue.push(x);
};

MyStack.prototype.pop = function() {
    let size = this.queue.length;
    while(size-- > 1) {
        this.queue.push(this.queue.shift());
    }
    return this.queue.shift();
};

MyStack.prototype.top = function() {
    const x = this.pop();
    this.queue.push(x);
    return x;
};
MyStack.prototype.empty = function() {
    return !this.queue.length;
};

150. 逆波兰表达式求值​

150. 逆波兰表达式求值

逆波兰表达式：是一种后缀表达式，所谓后缀就是指算符写在后面。

平常使用的算式则是一种中缀表达式，如 ( 1 + 2 ) * ( 3 + 4 ) 。

该算式的逆波兰表达式写法为 ( ( 1 2 + ) ( 3 4 + ) * ) 。

逆波兰表达式主要有以下两个优点：

  • 去掉括号后表达式无歧义，上式即便写成 1 2 + 3 4 + * 也可以依据次序计算出正确结果。
  • 适合用栈操作运算：遇到数字则入栈；遇到算符则取出栈顶两个数字进行计算，并将结果压入栈中
var evalRPN = function(tokens) {
    const s = new Map([
        ["+", (a, b) => a * 1  + b * 1],
        ["-", (a, b) => b - a],
        ["*", (a, b) => b * a],
        ["/", (a, b) => (b / a) | 0]
    ]);
    const stack = [];
    for (const i of tokens) {
        if(!s.has(i)) {
            stack.push(i);
            continue;
        }
        stack.push(s.get(i)(stack.pop(),stack.pop()))
    }
    return stack.pop();
};

1047. 删除字符串中的所有相邻重复项​

1047. 删除字符串中的所有相邻重复项

给出由小写字母组成的字符串 S，重复项删除操作会选择两个相邻且相同的字母，并删除它们。

在 S 上反复执行重复项删除操作，直到无法继续删除。

在完成所有重复项删除操作后返回最终的字符串。答案保证唯一。

栈: 1.初始化栈并循环字符串S 2.如果字符串S[i]和栈顶元素相同,则出栈,否则入栈 3.返回栈的字符串格式

var removeDuplicates = function (S) {
    let stack = [];
    for (let i = 0, sLen = S.length; i < sLen; i++) {
        if (stack.length && stack[stack.length - 1] === S[i]) {
            stack.pop();
        } else {
            stack.push(S[i]);
        }
    }
    return stack.join('');
};

347.前 K 个高频元素​

347. 前 K 个高频元素

大顶堆（堆头是最大元素），小顶堆（堆头是最小元素），c++可以直接用priority_queue（优先级队列），底层实现都是一样的，从小到大排就是小顶堆，从大到小排就是大顶堆。

要用小顶堆，因为要统计最大前k个元素，只有小顶堆每次将最小的元素弹出，最后小顶堆里积累的才是前k个最大元素。

如果是排序，求升序用大顶堆，求降序用小顶堆。 一般我们说 topK 问题，就可以用大顶堆或小顶堆来实现， 最大的 K 个：小顶堆 最小的 K 个：大顶堆

let topKFrequent = function (nums, k) {
    let map = new Map(), heap = [,]
    nums.map((num) => {
        if (map.has(num)) map.set(num, map.get(num) + 1)
        else map.set(num, 1)
    })

    // 如果元素数量小于等于 k
    if (map.size <= k) {
        return [...map.keys()]
    }

    // 如果元素数量大于 k，遍历map，构建小顶堆
    let i = 0
    map.forEach((value, key) => {
        if (i < k) {
            // 取前k个建堆, 插入堆
            heap.push(key)
            
            // 原地建立前 k 堆
            if (i === k - 1) buildHeap(heap, map, k)
        } else if (map.get(heap[1]) < value) {
            // 替换并堆化
            heap[1] = key
            // 自上而下式堆化第一个元素
            heapify(heap, map, k, 1)
        }
        i++
    })
    // 删除heap中第一个元素
    heap.shift()
    return heap
};

// 原地建堆，从后往前，自上而下式建小顶堆
let buildHeap = (heap, map, k) => {
    if (k === 1) return
    // 从最后一个非叶子节点开始，自上而下式堆化
    for (let i = Math.floor(k / 2); i >= 1; i--) {
        heapify(heap, map, k, i)
    }
}

// 堆化
let heapify = (heap, map, k, i) => {
    // 自上而下式堆化
    while (true) {
        let minIndex = i
        if (2 * i <= k && map.get(heap[2 * i]) < map.get(heap[i])) {
            minIndex = 2 * i
        }
        if (2 * i + 1 <= k && map.get(heap[2 * i + 1]) < map.get(heap[minIndex])) {
            minIndex = 2 * i + 1
        }
        if (minIndex !== i) {
            swap(heap, i, minIndex)
            i = minIndex
        } else {
            break
        }
    }
}

// 交换
let swap = (arr, i, j) => {
    let temp = arr[i]
    arr[i] = arr[j]
    arr[j] = temp
}

739. 每日温度​

739. 每日温度

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

输入: temperatures = [73,74,75,71,69,72,76,73] 输出: [1,1,4,2,1,1,0,0]

维护一个单调栈 记录下标

image-20221008202942438

    function dailyTemperatures(temperatures){
      let n = temperatures.length;
      let res = new Array(n).fill(0);
    
      // 单调栈
      let stack = [0]
    
      // 遍历每日温度，维护一个单调栈
      for (let i = 1; i < n; i++) {
        // 当日温度大于栈顶温度，说明栈顶温度的升温日找到了，栈顶出栈并计算天数；继续判断栈顶元素
        while (stack.length && temperatures[i] > temperatures[stack[stack.length - 1]]) {
          const top = stack.pop()
          res[top] = i - top
        }
        // 栈为空 或 每日温度小于等于栈顶温度 => 直接入栈
        stack.push(i)
      }
    
      return res;
    };

496.下一个更大元素 I​

496. 下一个更大元素 I

nums1 中数字 x 的 下一个更大元素 是指 x 在 nums2 中对应位置 右侧 的 第一个 比 x 大的元素。

给你两个 没有重复元素 的数组 nums1 和 nums2 ，下标从 0 开始计数，其中nums1 是 nums2 的子集。

对于每个 0 <= i < nums1.length ，找出满足 nums1[i] == nums2[j] 的下标 j ，并且在 nums2 确定 nums2[j] 的 下一个更大元素 。如果不存在下一个更大元素，那么本次查询的答案是 -1 。

返回一个长度为 nums1.length 的数组 ans 作为答案，满足 ans[i] 是如上所述的 下一个更大元素 。

输入: nums1 = [4,1,2], nums2 = [1,3,4,2]. 输出: [-1,3,-1] 解释: 对于 num1 中的数字 4 ，你无法在第二个数组中找到下一个更大的数字，因此输出 -1 。 对于 num1 中的数字 1 ，第二个数组中数字1右边的下一个较大数字是 3 。 对于 num1 中的数字 2 ，第二个数组中没有下一个更大的数字，因此输出 -1 。

在739. 每日温度中是求每个元素下一个比当前元素大的元素的位置。

本题则是说nums1 是 nums2的子集，找nums1中的元素在nums2中下一个比当前元素大的元素。

var nextGreaterElement = function (nums1, nums2) {
  let stack = [];
  let map = new Map();
  for (let i = 0; i < nums2.length; i++) {
    while (stack.length && nums2[i] > nums2[stack[stack.length - 1]]) {
      let index = stack.pop();
      map.set(nums2[index], nums2[i]);
    }
    stack.push(i);
  }

  let res = [];
  for (let j = 0; j < nums1.length; j++) {
    res[j] = map.get(nums1[j]) || -1;
  }

  return res;
};

503.下一个更大元素II​

503. 下一个更大元素 II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:

  • 输入: [1,2,1]
  • 输出: [2,-1,2]
  • 解释: 第一个 1 的下一个更大的数是 2；数字 2 找不到下一个更大的数；第二个 1 的下一个最大的数需要循环搜索，结果也是 2。

在遍历的过程中模拟走了两边nums

var nextGreaterElements = function (nums) {
  const len = nums.length;
  let stack = [];
  let res = Array(len).fill(-1);
  for (let i = 0; i < len * 2; i++) {
    while (
      stack.length &&
      nums[i % len] > nums[stack[stack.length - 1]]
    ) {
      const index = stack.pop();
      res[index] = nums[i % len];
    }
    stack.push(i % len);
  }
  return res;
};

哈希表​

1. 两数之和​

var twoSum = function (nums, target) {
    const map = new Map()
    for (let i = 0; i < nums.length; i++) {
        const num = nums[i]
        const mid = target - num
        // 查询值为 target - num 的元素
        if (map.has(mid)) {
            // 找到了，直接返回这两个数的下标
            return [map.get(mid), i]
        }
        // 将值记录下来
        map.set(num, i)
    }
};

242.有效的字母异位词​

242. 有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

示例 1: 输入: s = "anagram", t = "nagaram" 输出: true

示例 2: 输入: s = "rat", t = "car" 输出: false

说明: 你可以假设字符串只包含小写字母。

输入: s = "anagram", t = "nagaram" 输出: true

var isAnagram = function(s, t) {
    if(s.length !== t.length) return false;
    const resSet = new Array(26).fill(0);
    const base = "a".charCodeAt();
    for(const i of s) {
        resSet[i.charCodeAt() - base]++;
    }
    for(const i of t) {
        if(!resSet[i.charCodeAt() - base]) return false;
        resSet[i.charCodeAt() - base]--;
    }
    return true;
};

map

js用map解决，s,,t为异位词，t中的元素必定存在s中，只是位置不同而已，利用map进行遍历判断： 1.建立一个s字符串的Map,每一个元素设置键值1,重复出现的元素键值+1 2.遍历判断t中的元素在s中是否有且键值大于0（大于零表示存在的） 3.每找到一个元素，其键值-1（用于标记其已经被找过了，下次对比不找它了）

var isAnagram = function(s, t) {

    if(s.length!=t.length){  //长度不想的的直接返回false
        return false;
    }

     var map = new Map();   //新建map集合
     for (var n of s) {      //将s放入Map集合中，并标记他们出现的次数通过set
         if (map.has(n)) {
             map.set(n, map.get(n) + 1); //重复出现元素键值+1，用于计数标记
         } else {
             map.set(n, 1);         //键值设为1
         }
     }

     for (var n of t) {            
         if (map.has(n) && map.get(n) > 0) { //遍历判断t中元素在s中是否存在
               map.set(n, map.get(n) - 1);   //没找到一个，键值-1；
         }else{                     
             return false;
         }
     }                                     
    return true; //循环结束后为s与t异位,必定t中的元素在s的map中都能找到
     
};

349. 两个数组的交集​

349. 两个数组的交集

var intersection = function(nums1, nums2) {
        //使用set求交集
        var a = new Set(nums1);
        var b = new Set();
        for(let n of nums2){
            if(a.has(n)){
                b.add(n)
            }
        }
        return [...b]
};

202. 快乐数​

202. 快乐数

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。 如果这个过程 结果为 1，那么这个数就是快乐数。 如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

输入：n = 19 输出：true 解释： 12 + 92 = 82 82 + 22 = 68 62 + 82 = 100 12 + 02 + 02 = 1

双指针法

let getNext=function(n) {
    return n.toString().split('').map(i => i ** 2).reduce((a, b) => a + b)
}
var isHappy = function(n) {
  let slow=n;
    let fast=getNext(n)
    while(fast!==1&&fast!==slow){
        slow = getNext(slow);
        fast = getNext(getNext(fast));
    }
    return fast === 1;
};

使用set

var getSum = function (n) {
    let sum = 0;
    while (n) {
        sum += (n % 10) ** 2;
        n =  Math.floor(n/10);
    }
    return sum;
}
var isHappy = function(n) {
    let set = new Set();   // Set() 里的数是惟一的
    // 如果在循环中某个值重复出现，说明此时陷入死循环，也就说明这个值不是快乐数
    while (n !== 1 && !set.has(n)) {
        set.add(n);
        n = getSum(n);
    }
    return n === 1;
};

//使用Set()，求和用reduce
var isHappy = function(n) {
    let set = new Set();
    let totalCount;
    while(totalCount !== 1) {
        let arr = (''+(totalCount || n)).split('');
        totalCount = arr.reduce((total, num) => {
            return total + num * num
        }, 0)
        if (set.has(totalCount)) {
            return false;
        }
        set.add(totalCount);
    }
    return true;
};

454.四数相加II​

454. 四数相加 II

给你四个整数数组 nums1、nums2、nums3 和 nums4 ，数组长度都是 n ，请你计算有多少个元组 (i, j, k, l) 能满足：

0 <= i, j, k, l < n nums1[i] + nums2[j] + nums3[k] + nums4[l] == 0

var fourSumCount = function(nums1, nums2, nums3, nums4) {
    const twoSumMap = new Map();
    let count = 0;

    for(const n1 of nums1) {
        for(const n2 of nums2) {
            const sum = n1 + n2;
            twoSumMap.set(sum, (twoSumMap.get(sum) || 0) + 1)
        }
    }

    for(const n3 of nums3) {
        for(const n4 of nums4) {
            const sum = n3 + n4;
            count += (twoSumMap.get(0 - sum) || 0)
        }
    }

    return count;
};

383. 赎金信​

383. 赎金信

给你两个字符串：ransomNote 和 magazine ，判断 ransomNote 能不能由 magazine 里面的字符构成。

如果可以，返回 true ；否则返回 false 。

magazine 中的每个字符只能在 ransomNote 中使用一次。

使用一个对象临时存储值，时间复杂度 O(2n)，空间复杂度O(n)

var canConstruct = function(ransomNote, magazine) {
    const store = {}
    for(let i = 0; i < magazine.length; i ++) {
        if(!store[[magazine[i]]]) {
            store[magazine[i]] = 1
        }else {
            store[magazine[i]] ++
        }
    }
    for(let i = 0; i < ransomNote.length; i ++) {
        if(store[ransomNote[i]]){
            store[ransomNote[i]] --
        }else{
            return false
        }
    }
    return true
};

图论​

133. 克隆图​

133. 克隆图

DFS

深度优先搜索，使用hash来记录已被遍历过的节点，防止进入死循环

function Node(val, neighbors) {
   this.val = val === undefined ? 0 : val;
   this.neighbors = neighbors === undefined ? [] : neighbors;
};
var cloneGraph = function(node) {
    if(!node) return;
    const visited = new Map();
    const dfs = (n) => {
        const nCopy = new Node(n.val);
        visited.set(n, nCopy);
        (n.neighbors || []).forEach(ne => {
            if(!visited.has(ne)) {
                dfs(ne);
            }
            nCopy.neighbors.push(visited.get(ne));
        })
    }
    dfs(node);
    return visited.get(node);
};

BFS

广度优先搜索，使用hash来记录已被遍历过的节点，防止进入死循环。

function Node(val, neighbors) {
   this.val = val === undefined ? 0 : val;
   this.neighbors = neighbors === undefined ? [] : neighbors;
};
var cloneGraph = function(node) {
    if(!node) return;
    const visited = new Map();
    visited.set(node, new Node(node.val));
    const q = [node];
    while(q.length) {
        const n = q.shift()
        console.log(n.val);
        (n.neighbors || []).forEach(ne => {
            if(!visited.has(ne)) {
                q.push(ne);
                visited.set(ne, new Node(ne.val));
            }
            visited.get(n).neighbors.push(visited.get(ne));
        })
    }
    return visited.get(node);
};

207. 课程表​

207. 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。 请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

题意解释 一共有 n 门课要上，编号为 0 ~ n-1。 先决条件[1, 0]，意思是必须先上课 0，才能上课 1。 给你 n 、和一个先决条件表，请你判断能否完成所有课程。 再举个生活的例子 先穿内裤再穿裤子，先穿打底再穿外套，先穿衣服再戴帽子，是约定俗成的。 内裤外穿、光着身子戴帽子等，都会有点奇怪。 我们遵循穿衣的一条条先后规则，用一串顺序行为，把衣服一件件穿上。 我们遵循课程之间的先后规则，找到一种上课顺序，把所有课一节节上完。

用有向图描述依赖关系 示例：n = 6，先决条件表：[[3, 0], [3, 1], [4, 1], [4, 2], [5, 3], [5, 4]] 课 0, 1, 2 没有先修课，可以直接选。其余的课，都有两门先修课。 我们用有向图来展现这种依赖关系（做事情的先后关系）：

这种叫 有向无环图，把一个 有向无环图 转成 线性的排序 就叫 拓扑排序。 有向图有 入度 和 出度 的概念： 如果存在一条有向边 A --> B，则这条边给 A 增加了 1 个出度，给 B 增加了 1 个入度。 所以，顶点 0、1、2 的入度为 0。顶点 3、4、5 的入度为 2。 每次只能选你能上的课 每次只能选入度为 0 的课，因为它不依赖别的课，是当下你能上的课。 假设选了 0，课 3 的先修课少了一门，入度由 2 变 1。 接着选 1，导致课 3 的入度变 0，课 4 的入度由 2 变 1。 接着选 2，导致课 4 的入度变 0。 现在，课 3 和课 4 的入度为 0。继续选入度为 0 的课……直到选不到入度为 0 的课。

让入度为 0 的课入列，它们是能直接选的课。 然后逐个出列，出列代表着课被选，需要减小相关课的入度。 如果相关课的入度新变为 0，安排它入列、再出列……直到没有入度为 0 的课可入列。

每门课的入度需要被记录，我们关心入度值的变化。 课程之间的依赖关系也要被记录，我们关心选当前课会减小哪些课的入度。 因此我们需要选择合适的数据结构，去存这些数据： 入度数组：课号 0 到 n - 1 作为索引，通过遍历先决条件表求出对应的初始入度。 邻接表：用哈希表记录依赖关系（也可以用二维矩阵，但有点大） key：课号 value：依赖这门课的后续课（数组） 怎么判断能否修完所有课？ BFS 结束时，如果仍有课的入度不为 0，无法被选，完成不了所有课。否则，能找到一种顺序把所有课上完。 或者：用一个变量 count 记录入列的顶点个数，最后判断 count 是否等于总课程数。

const canFinish = (numCourses, prerequisites) => {
  const inDegree = new Array(numCourses).fill(0); // 入度数组
  const map = {};                                 // 邻接表
  for (let i = 0; i < prerequisites.length; i++) {
    inDegree[prerequisites[i][0]]++;              // 求课的初始入度值
    if (map[prerequisites[i][1]]) {               // 当前课已经存在于邻接表
      map[prerequisites[i][1]].push(prerequisites[i][0]); // 添加依赖它的后续课
    } else {                                      // 当前课不存在于邻接表
      map[prerequisites[i][1]] = [prerequisites[i][0]];
    }
  }
  const queue = [];
  for (let i = 0; i < inDegree.length; i++) { // 所有入度为0的课入列
    if (inDegree[i] == 0) queue.push(i);
  }
  let count = 0;
  while (queue.length) {
    const selected = queue.shift();           // 当前选的课，出列
    count++;                                  // 选课数+1
    const toEnQueue = map[selected];          // 获取这门课对应的后续课
    if (toEnQueue && toEnQueue.length) {      // 确实有后续课
      for (let i = 0; i < toEnQueue.length; i++) {
        inDegree[toEnQueue[i]]--;             // 依赖它的后续课的入度-1
        if (inDegree[toEnQueue[i]] == 0) {    // 如果因此减为0，入列
          queue.push(toEnQueue[i]);
        }
      }
    }
  }
  return count == numCourses; // 选了的课等于总课数，true，否则false
};

总结：拓扑排序问题 根据依赖关系，构建邻接表、入度数组。 选取入度为 0 的数据，根据邻接表，减小依赖它的数据的入度。 找出入度变为 0 的数据，重复第 2 步。 直至所有数据的入度为 0，得到排序，如果还有数据的入度不为 0，说明图中存在环。

210. 课程表 II​

210. 课程表 II

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。 返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组

var findOrder = function(numCourses, prerequisites) {
    const inDegrees = Array(numCourses).fill(0);
    const res = [];
    const G = Array(numCourses).fill(0).map(_ => []);

    for (let e of prerequisites) {
        G[e[1]].push(e[0]);
        inDegrees[e[0]]++;
    }

    while (res.length < numCourses) {
        let hasCycle = true;

        for (let i = 0; i < numCourses; i++) {
            if (inDegrees[i] === 0) {
                hasCycle = false;
                inDegrees[i] = -1;
                res.push(i);

                for (let w of G[i]) {
                    inDegrees[w]--;
                }
            }
        }

        if (hasCycle) return [];
    }

    return res;
}

排序​

快速排序​

const partition=(arr)=>{
    let x=arr[0]
    let length=arr.length
    let i=0
    let j=length-1
    while(i<j){
        // 先从后往前找小的, 没找到继续找
        while(i<j&&arr[j]>x){
            j--;
        }    
        // 找到了，将a[j]值填入坑里, a[j]又变成了坑
        if(i<j){
            arr[i]=arr[j]
        }
        // 然后从前往后找大的，没找到继续找
        while(i<j&&arr[i]<x){
            i++
        }    
        // 找到了，将值填入之前的坑里
        if(i<j){
            arr[j]=arr[i];
        }
    }
    a[i]=x;
    return arr;

}
const a = [2, 1, 3, 6, 4, 5, 9, 8, 7];
let result = partition(a);
console.log(result);

215. 数组中的第K个最大元素​

215. 数组中的第K个最大元素

其实没有必要全部排序，可以利用快速排序的 partition 操作，找到第 K 个最大元素。

每进行一次快速排序的 partition 操作，就能找到这次我们选中的基准值排序之后的正确位置。

如果它的位置刚好是排序之后第 K 个最大元素的位置，即 len - k，我们直接得到了答案； 因为进行 partition 操作之后，位于基准值之前的元素都要小于基准值，位于基准值之后的元素都要大于等于基准值。

如果它的位置小于排序之后第 K 个最大元素的位置，我们就去它之后寻找第 K 个最大元素； 如果它的位置大于排序之后第 K 个最大元素的位置，我们就去它之前寻找第 K 个最大元素；

分治选择排序，然后修正位置

var findKthLargest = function (nums, k) {
  const len = nums.length;
  const targetIndex = len - k;
  let left = 0,right = len - 1;

  while (left < right) {
    const index = partition(nums, left, right);
    if (index === targetIndex) {
      return nums[index];
    } else if (index < targetIndex) {
      left = index + 1;
    } else {
      right = index - 1;
    }
  }

  return nums[left];
};

function partition(nums, start, end) {
  const povit = nums[start];
  while (start < end) {
    while (start < end && nums[end] >= povit) {
      end--;
    }
    nums[start] = nums[end];
    while (start < end && nums[start] < povit) {
      start++;
    }
    nums[end] = nums[start];
  }
  nums[start] = povit;
  return start;
}

165. 比较版本号​

165. 比较版本号

var compareVersion = function (version1, version2) {
    let v1 = version1.split(".");
    let v2 = version2.split(".");
    let len = Math.max(v1.length, v2.length)
    for (let i = 0; i <len ; i++) {
        let tempV1 = Number(v1[i] ?? 0)
        let tempV2 = Number(v2[i] ?? 0)
        if (tempV1 > tempV2) return 1;
        if (tempV1 < tempV2) return -1;
        // 如果相等则跳过继续进行循环
    }
    
    return 0;
};

215. 数组中的第K个最大元素​

215. 数组中的第K个最大元素

快排法

var findKthLargest = function (nums, k) {
  const len = nums.length;
  const targetIndex = len - k;
  let left = 0,
    right = len - 1;

  while (left < right) {
    const index = partition(nums, left, right);
    if (index === targetIndex) {
      return nums[index];
    } else if (index < targetIndex) {
      left = index + 1;
    } else {
      right = index - 1;
    }
  }

  return nums[left];
};

function partition(nums, start, end) {
  const povit = nums[start];
  while (start < end) {
    while (start < end && nums[end] >= povit) {
      end--;
    }
    nums[start] = nums[end];
    while (start < end && nums[start] < povit) {
      start++;
    }
    nums[end] = nums[start];
  }
  nums[start] = povit;
  return start;
}

  1. 合并区间​

56. 合并区间

var merge = function(intervals) {
        intervals.sort((a,b)=>a[0]-b[0])
        let prev=intervals[0]
        let result=[]
        for(let i=0;i<intervals.length;i++){
            let cur=intervals[i]
            if(cur[0]>prev[1]){
                result.push(prev)
                prev=cur
            }else{
                prev[1]=Math.max(cur[1],prev[1])
            }
        }
        result.push(prev)
        return result
};

31. 下一个排列​

31. 下一个排列

整数数组的 下一个排列 是指其整数的下一个字典序更大的排列

  • 例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。
  • 类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。

思路：从后往前遍历 如果遇到后一个大于前一个就跳出 并记录下标j

然后再对j~length 进行遍历 如果发现比之前大的就进行一个交换 大的数换到前面

j右边的数进行翻转，使得变大的幅度小一些

var nextPermutation = function(nums) {
    let j = -1;
    for(let i = nums.length - 2 ; i >= 0; i --) {
        if(nums[i] < nums[i + 1]) {
            j = i;
            break;
        }
    }
    if(j == -1) 
      //如果 j = -1，说明是递减排列
        nums.reverse();
    else {
        for(let i = nums.length - 1; i > j; i --) {
            if(nums[i] > nums[j]) {
                [nums[i], nums[j]] = [nums[j], nums[i]];
                break;
            }
        }
        let i = j + 1, k = nums.length - 1;
        while(i < k) {
            [nums[i], nums[k]] = [nums[k], nums[i]];
            i ++, k --;
        }
    }
};

148. 排序链表​

148. 排序链表

// 归并排序
var sortList = function (head) {
  if (!head || head.next === null) return head;
  // 使用快慢指针找到中间节点
  let slow = head,
    fast = head.next;
  while (fast !== null && fast.next !== null) {
    slow = slow.next;
    fast = fast.next.next;
  }
  // 将链表分成两半并返回后半部分链表的头节点
  let newList = slow.next;
  slow.next = null;

  // 对前后两个链表进行排序
  let left = sortList(head);
  let right = sortList(newList);
  // 将排序好的两个有序链表合并为一个链表
  let res = new ListNode(-1);
  let nHead = res;
  // 合并链表只需要调整指针的指向
  // 两个链表哪个节点的值小就先指向它
  while (left !== null && right !== null) {
    if (left.val < right.val) {
      nHead.next = left;
      left = left.next;
    } else {
      nHead.next = right;
      right = right.next;
    }
    nHead = nHead.next;
  }
  nHead.next = left === null ? right : left;
  return res.next;
};

4. 寻找两个正序数组的中位数​

4. 寻找两个正序数组的中位数

先将两数组排序，然后根据两数组长度判断，中位数取一个还是两个平均值，返回结果。

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

var findMedianSortedArrays = function(nums1, nums2) {
    let len1 = nums1.length;
    let len2 = nums2.length;
    let middle;
    let flag;
    if ((len1 + len2) % 2 === 0) {
        middle = parseInt((len1+len2)/2);
        flag = 0;
    } else {
        middle = parseInt((len1+len2)/2) + 1;
        flag = 1;
    }
    let i=0, j=0;
    let arr = [];
    while(i < len1 && j < len2) {
        if (nums1[i] < nums2[j]) {
            arr.push(nums1[i]);
            i++;
        } else {
            arr.push(nums2[j]);
            j++;
        }
    }
    if (i === len1) {
        arr = arr.concat(nums2.slice(j));
    }

    if (j === len2) {
        arr = arr.concat(nums1.slice(i));
    }

    if (flag === 0) {
        return parseFloat((arr[middle-1] + arr[middle]) / 2);
    } else {
        return arr[middle-1];
    }
};

41. 缺失的第一个正数​

41. 缺失的第一个正数

给你一个未排序的整数数组 nums ，请你找出其中没有出现的最小的正整数。

请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。

1.首先将nums[i]放到对应的位置，如nums[0] = 1，nums[1] = 2，....，nums[6] = 7 2.然后遍历交换位置之后的数组，判断是否是对应位置，若不是，则直接返回当前索引值 + 1；若全都是，则直接返回nums.length + 1即可

var firstMissingPositive = function(nums) {
    for(let i = 0; i < nums.length; i++) {
        // 循环nums，当前元素在(0,nums.length]之间，并且nums[nums[i]-1] != nums[i]，则交换位置
        while(nums[i] > 0 && nums[i] <= nums.length && nums[nums[i]-1] != nums[i]) {
            const temp = nums[nums[i]-1];
            nums[nums[i]-1] = nums[i];
            nums[i] = temp;
        }
    }
    for(let i = 0; i < nums.length; i++) {// 循环交换位置之后的数组，判断第一个缺失的正数
        if(nums[i] != i+1) {
            return i+1;
        }
    }
    // [1,2,3]
    return nums.length + 1;
};

分治​

704. 二分查找​

704. 二分查找

var search = function (nums, target) {
    let l = 0, r = nums.length - 1;
    while (l <= r) {
        let mid = (l + r) >> 1;
        if (nums[mid] === target) return mid;
        let isSmall = nums[mid] < target;
        l = isSmall ? mid + 1 : l;
        r = isSmall ? r : mid - 1;
    }

    return -1;
};

852. 山脉数组的峰顶索引​

852. 山脉数组的峰顶索引

var peakIndexInMountainArray = function(arr) {
  let left = 1,
    right = arr.length - 1;
  // 左闭右闭区间
  while (left <= right) {
    // 中间值  下面这样写是防止大数情况下溢出
    let mid = left + ((right - left) >> 1);
    // 如果这个数字比它前后两个数字都大
    if (arr[mid] > arr[mid + 1] && arr[mid] > arr[mid - 1]) {
      return mid;
    }
    // 如果这个数字比它前一个数字大，但比后一个数字小，那么这个数字位于数组递增的部分，
    // 数组的最大值一定在它的后面
    if (arr[mid] > arr[mid - 1]) {
      left = mid + 1;
    } else {
      // 如果这个数字比它前一个数字小，但比后一个数字大，那么这个数字位于数组递减的部分，
      // 数组的最大值一定在它的前面
      right = mid - 1;
    }
  }
  return -1;
};

69. x 的平方根​

69. x 的平方根

给你一个非负整数 x ，计算并返回 x 的 算术平方根 。

由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。

var mySqrt = function(x) {
    let left=1,right=x;
    while(left<=right){
        let mid=left+((right-left)>>1)
        if(mid<=x/mid){
            if(mid+1>x/(mid+1)){
                return mid
            }
            left=mid+1
        }else{
            right=mid-1
        }
    }
    return 0;
};

递归​

递归求1-100的和​

//正常递归
function sum(n){
    if(n == 1){
        return 1;
       }
    return sum(n - 1) + n;
}
console.log(sum(100));


//尾递归
function add (n,sum){
    if(n<=0) return sum
    return add(n-1,n+sum)
}
add(100,0)

200. 岛屿数量​

200. 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

DFS​

思路：循环网格，深度优先遍历每个坐标的四周，注意坐标不要越界，遇到陆地加1，并沉没四周的陆地，这样就不会重复计算 复杂度：时间复杂度O(mn), m和n是行数和列数。空间复杂度是O(mn),最坏的情况下所有网格都需要递归，递归栈深度达到m * n

const numIslands=(grid)=>{
    let count=0;
    for(let i=0;i<grid.length;i++){
        for(let j=0;j<grid[0].length;j++){
            if(grid[i][j]=='1'){
                count++;
                turnZero(i,j,grid)
            }
        }
    }
    return count
}
function turnZero(i,j,grid){
    if(i<0||i>=grid.length||j<0||j>=grid[0].length||grid[i][j]==='0')  return 
    grid[i][j]='0';
    turnZero(i,j+1,grid)
    turnZero(i,j-1,grid)
    turnZero(i+1,j,grid)
    turnZero(i-1,j,grid)
}

BFS​

思路：循环网格，广度优先遍历坐标的四周，遇到陆地加1，沉没四周的陆地，不重复计算陆地数 复杂度：时间复杂度O(mn),m和n是行数和列数。空间复杂度是O(min(m，n)),队列的长度最坏的情况下需要能容得下m和n中的较小者

const numIslands=(grid)=>{
    let count=0
    let queue=[]
    for(let i=0;i<grid.length;i++){
        for(let j=0;j<grid[0].length;j++){
            if(grid[i][j]==='1'){
                count++
                grid[i][j] = '0' // 做标记，避免重复遍历
                queue.push([i, j]) //加入队列
                turnZero(queue, grid)
            }
        }
    }
    return count
}

function turnZero(queue,grid){
    const dirs=[[0,1],[1,0],[0,-1],[-1,0]] //上 右 下 左
    while(queue.length){
        const cur=queue.shift()
        for (const dir of dirs) {  //四个方向广度优先扩散
            const x=cur[0]+dir[0]
            const y=cur[1]+dir[1]
            if (x < 0 || x >= grid.length || y < 0 || y >= grid[0].length || grid[x][y] !== '1') {
                continue
            }//检查坐标合法性
            grid[x][y]='0' //沉迷陆地
            queue.push([x,y])
        }
    }
}

695. 岛屿的最大面积​

695. 岛屿的最大面积

DFS​

var maxAreaOfIsland = function(grid) {
        let row =grid.length,col=grid[0].length
        function dfs(x,y){
        if(x<0||x>=row||y<0||y>=col||grid[x][y]===0) return 0
            grid[x][y]=0
            let ans=1,dx=[-1,1,0,0],dy=[0,0,1,-1]
            for(let i=0;i<dx.length;i++){
                ans+=dfs(x+dx[i],y+dy[i])
            }
            return ans
        }
        let res=0
        for(let i=0;i<row;i++){
            for(let j=0;j<col;j++){
                res=Math.max(res,dfs(i,j))
            }
        }
        return res
};

var maxAreaOfIsland = function(grid) {
    let max = 0;
    let count = 0;
    function dfs(row, col) {
        if(row < 0 || row >= grid.length || col < 0 || col >= grid[0].length || grid[row][col] === 0) {
            return 0;
        }
        grid[row][col] = 0;
        count = 1
        count += dfs(row+1, col)
        count += dfs(row-1, col)
        count += dfs(row, col+1)
        count += dfs(row, col-1)
        return count;
    }
    for(let i = 0; i < grid.length; i++) {
        for(let j = 0; j < grid[0].length; j++){
            if(grid[i][j] === 1) {
                max = Math.max(max, dfs(i, j))
            }
        }
    }
    return max;
};

BFS​

var maxAreaOfIsland = function(grid) {
  const m = grid.length;
  const n = grid[0].length;
  let maxArea = 0;
  for (let i = 0; i < m; i++) {
    for (let j = 0; j < n; j++) {
      if (grid[i][j] === 1) {
        const queue = [[i, j]];
        grid[i][j] = 0;
        let area = 0;
        while (queue.length) {
          const [curI, curJ] = queue.shift();
          area++;
          [[-1, 0], [0, 1], [1, 0], [0, -1]].forEach(item => {
            const x = curI + item[0];
            const y = curJ + item[1];
            if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] === 1) {
              queue.push([x, y]);
              grid[x][y] = 0;
            }
          });
        }
        maxArea = Math.max(maxArea, area);
      }
    }
  }
  return maxArea;
};

22. 括号生成​

22. 括号生成

数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

var generateParenthesis = function(n) {
        const res=[];
        var dfs=(LRemain,RRemain,str)=>{
            if(str.length==2*n){
                res.push(str);
                return;
            }
            //裁剪
            if(LRemain>0){
                dfs(LRemain-1,RRemain,str+"(");

            }
            if(LRemain<RRemain){
                dfs(LRemain,RRemain-1,str+")");
            }
        }
        dfs(n,n,"");
        return res;
};

回溯​

回溯法，一般可以解决如下几种问题：

  • 组合问题：N个数里面按一定规则找出k个数的集合
  • 切割问题：一个字符串按一定规则有几种切割方式
  • 子集问题：一个N个数的集合里有多少符合条件的子集
  • 排列问题：N个数按一定规则全排列，有几种排列方式
  • 棋盘问题：N皇后，解数独等等

组合是不强调元素顺序的，排列是强调元素顺序

回溯的过程

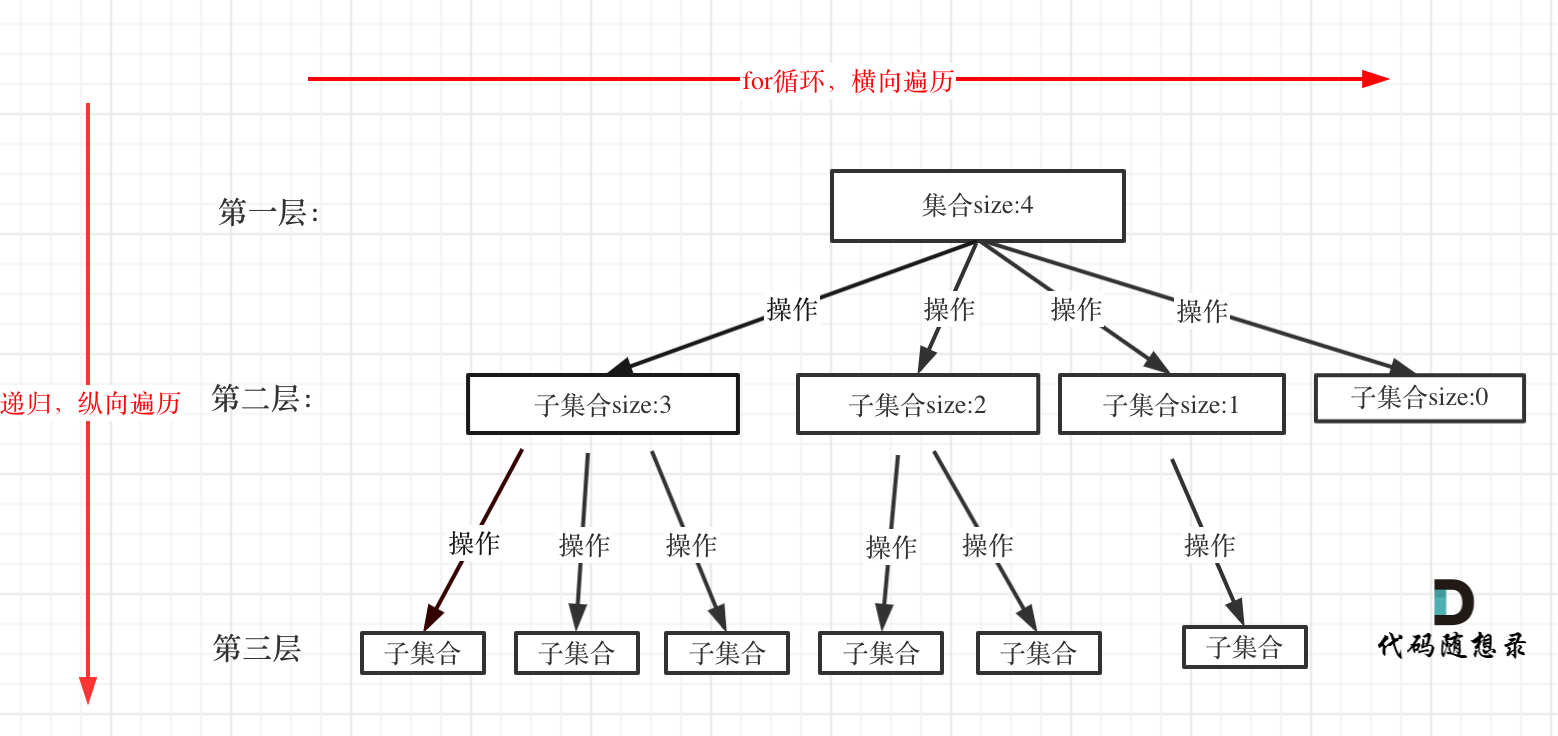
回溯算法理论基础

回溯函数遍历过程伪代码如下：

for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
    处理节点;
    backtracking(路径，选择列表); // 递归
    回溯，撤销处理结果
}

for循环就是遍历集合区间，可以理解一个节点有多少个孩子，这个for循环就执行多少次。

backtracking这里自己调用自己，实现递归。

大家可以从图中看出for循环可以理解是横向遍历，backtracking（递归）就是纵向遍历，这样就把这棵树全遍历完了，一般来说，搜索叶子节点就是找的其中一个结果了。

function backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

77. 组合​

给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按 任何顺序 返回答案。

输入：n = 4, k = 2 输出： [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]

递归

var combine = function(n, k) {
    let ret = []
    const helper = (start, prev) => {
        for(let i = start; i <= n; i++) { // 第一层
            const cur = prev.concat(i)
            if (cur.length === k) { // 出口条件
                ret.push(cur)
            } else {
                helper(i + 1, cur) // 第二层
            }
        }
    }
    helper(1, [])
    return ret
};

优化(剪枝)

优化过程如下：

  1. 已经选择的元素个数：path.size();
  2. 还需要的元素个数为: k - path.size();
  3. 在集合n中至多要从该起始位置 : n - (k - path.size()) + 1，开始遍历

为什么有个+1呢，因为包括起始位置，我们要是一个左闭的集合。

举个例子，n = 4，k = 3， 目前已经选取的元素为0（path.size为0），n - (k - 0) + 1 即 4 - ( 3 - 0) + 1 = 2。

从2开始搜索都是合理的，可以是组合[2, 3, 4]。

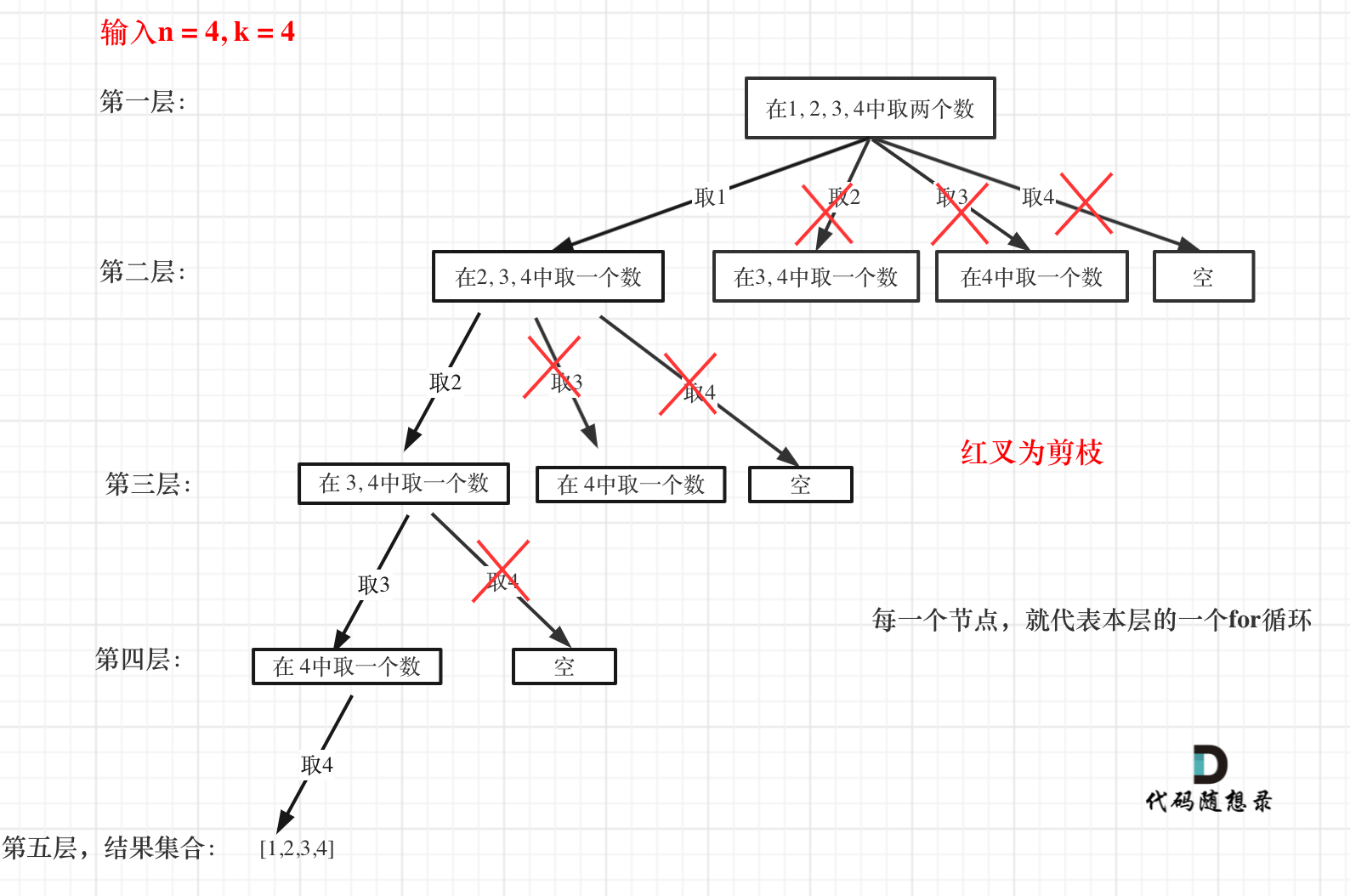
77.组合4

let result = []
let path = []
var combine = function(n, k) {
  result = []
  combineHelper(n, k, 1)
  return result
};
const combineHelper = (n, k, startIndex) => {
  if (path.length === k) {
    result.push([...path])
    return
  }
  for (let i = startIndex; i <= n - (k - path.length) + 1; ++i) {
    path.push(i)
    combineHelper(n, k, i + 1)
    path.pop()
  }
}

216. 组合总和 III​

216. 组合总和 III

找出所有相加之和为 n 的 k 个数的组合，且满足下列条件：

只使用数字1到9 每个数字 最多使用一次 返回 所有可能的有效组合的列表 。该列表不能包含相同的组合两次，组合可以以任何顺序返回。

var combinationSum3 = function (k, n) {
    let result = [];
    let path = [];
    var backtracking = function (targetSum, k, sum, startIndex) {
        if (path.length === k) {
            if (sum === targetSum) result.push(Array.from(path));
            return;
        }
        for (let i = startIndex; i <= 9 - (k - path.length) + 1; i++) {
            sum += i;
            path.push(i);
            backtracking(targetSum, k, sum, i + 1);
            sum -= i;
            path.pop();
        }
    }

    backtracking(n, k, 0, 1);
    return result;
};

17. 电话号码的字母组合​

17. 电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。答案可以按 任意顺序 返回。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例: 输入："23" 输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

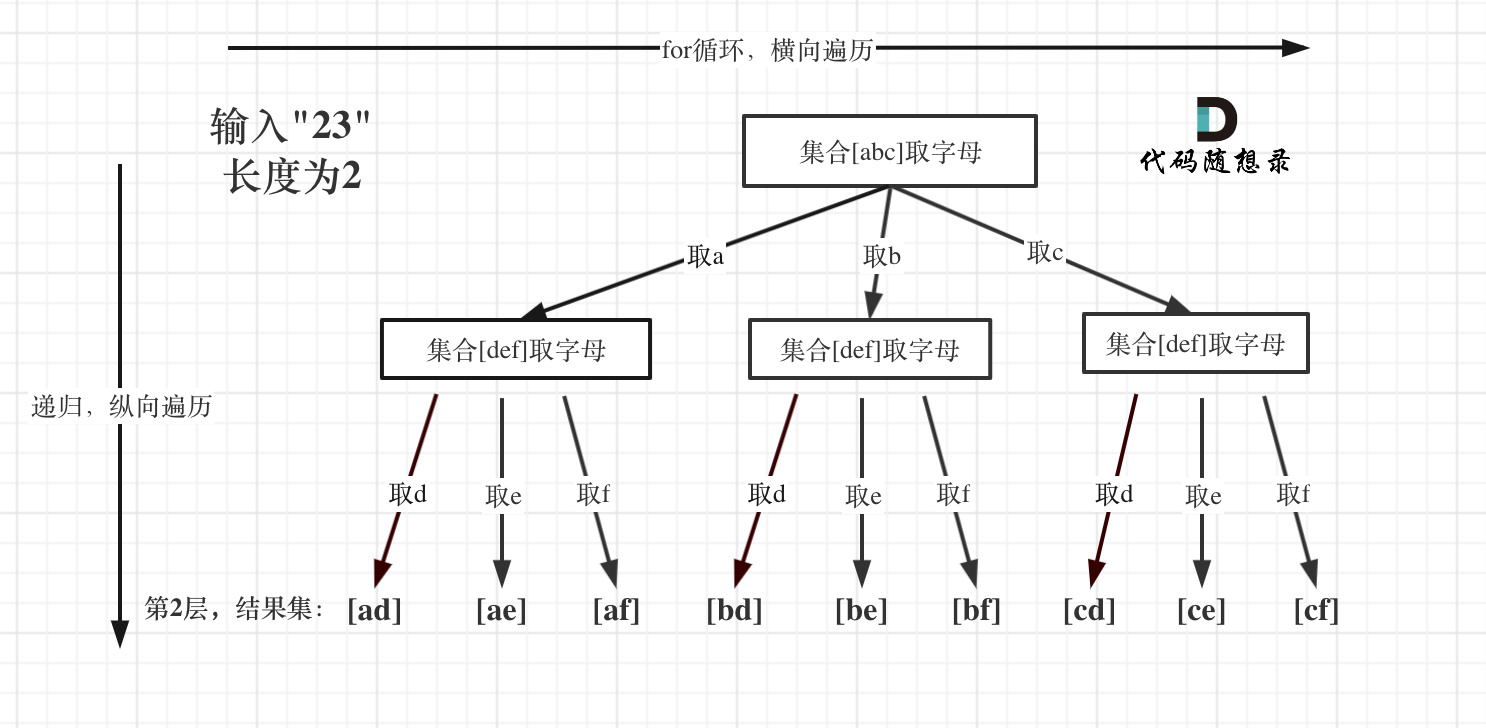
17. 电话号码的字母组合

var letterCombinations = function(digits) {
    const k = digits.length;
    const map = ["","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"];
    if(!k) return [];
    if(k === 1) return map[digits].split("");

    const res = [], path = [];
    backtracking(digits, k, 0);
    return res;

    function backtracking(n, k, a) {
        if(path.length === k) {
            res.push(path.join(""));
            return;
        }
        for(const v of map[n[a]]) {
            path.push(v);
            backtracking(n, k, a + 1);
            path.pop();
        }

    }
};

39. 组合总和​

39. 组合总和

给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ，找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ，并以列表形式返回。你可以按 任意顺序 返回这些组合。

candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同，则两种组合是不同的。

对于给定的输入，保证和为 target 的不同组合数少于 150 个。

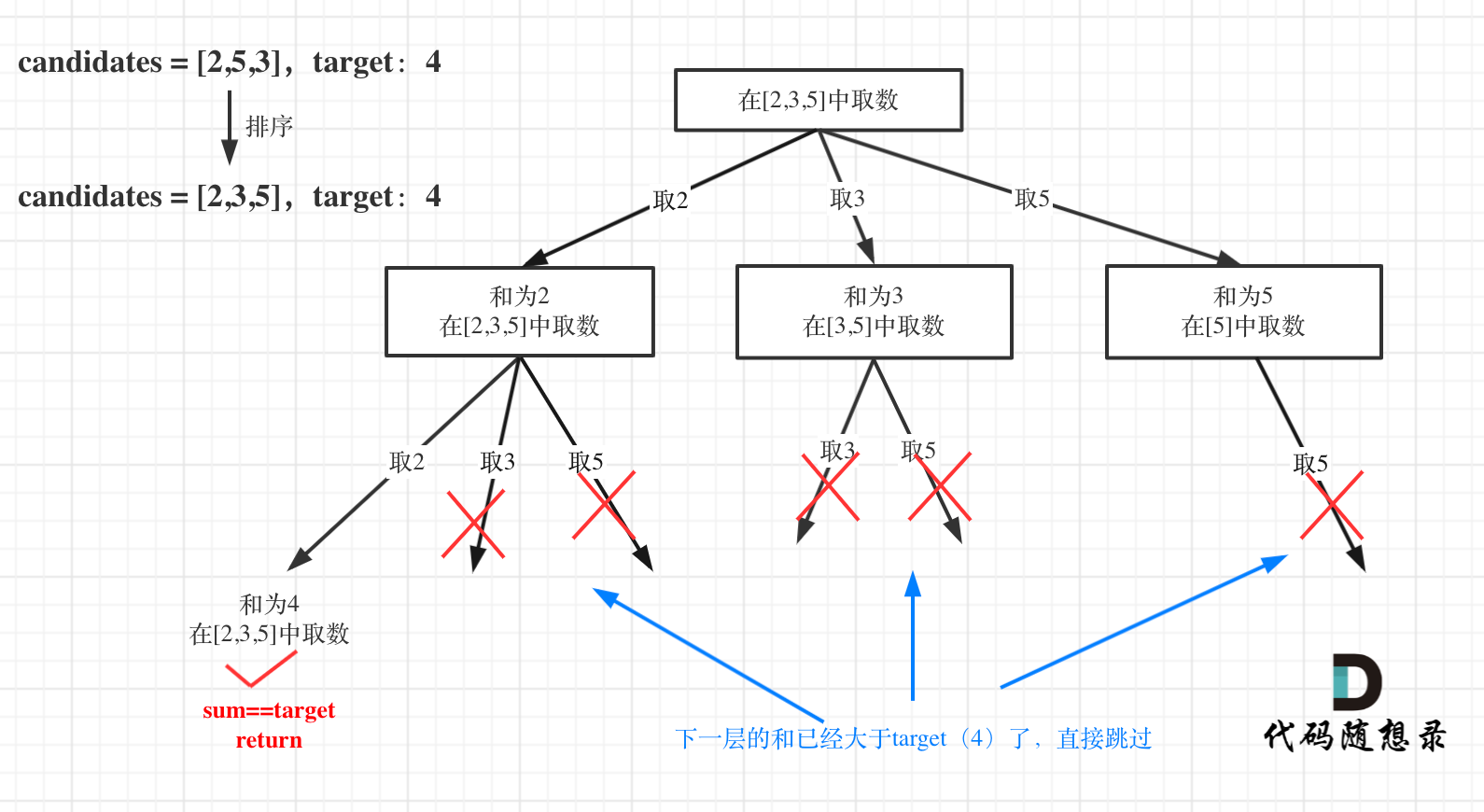
39.组合总和1

var combinationSum = function(candidates, target) {
    const res = [], path = [];
    candidates.sort((a,b)=>a-b); // 排序
    backtracking(0, 0);
    return res;
    function backtracking(j, sum) {
        if (sum === target) {
            res.push(Array.from(path));
            return;
        }
        for(let i = j; i < candidates.length; i++ ) {
            const n = candidates[i];
            if(n > target - sum) break;
            path.push(n);
            sum += n;
            backtracking(i, sum);
            path.pop();
            sum -= n;
        }
    }
};

40.组合总和II​

40. 组合总和 II

给定一个候选人编号的集合 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用 一次 。有重复元素

注意：解集不能包含重复的组合。

集合（数组candidates）有重复元素，但还不能有重复的组合。

与39.组合总和套路相同，此题还需要加一个bool型数组used，用来记录同一树枝上的元素是否使用过。

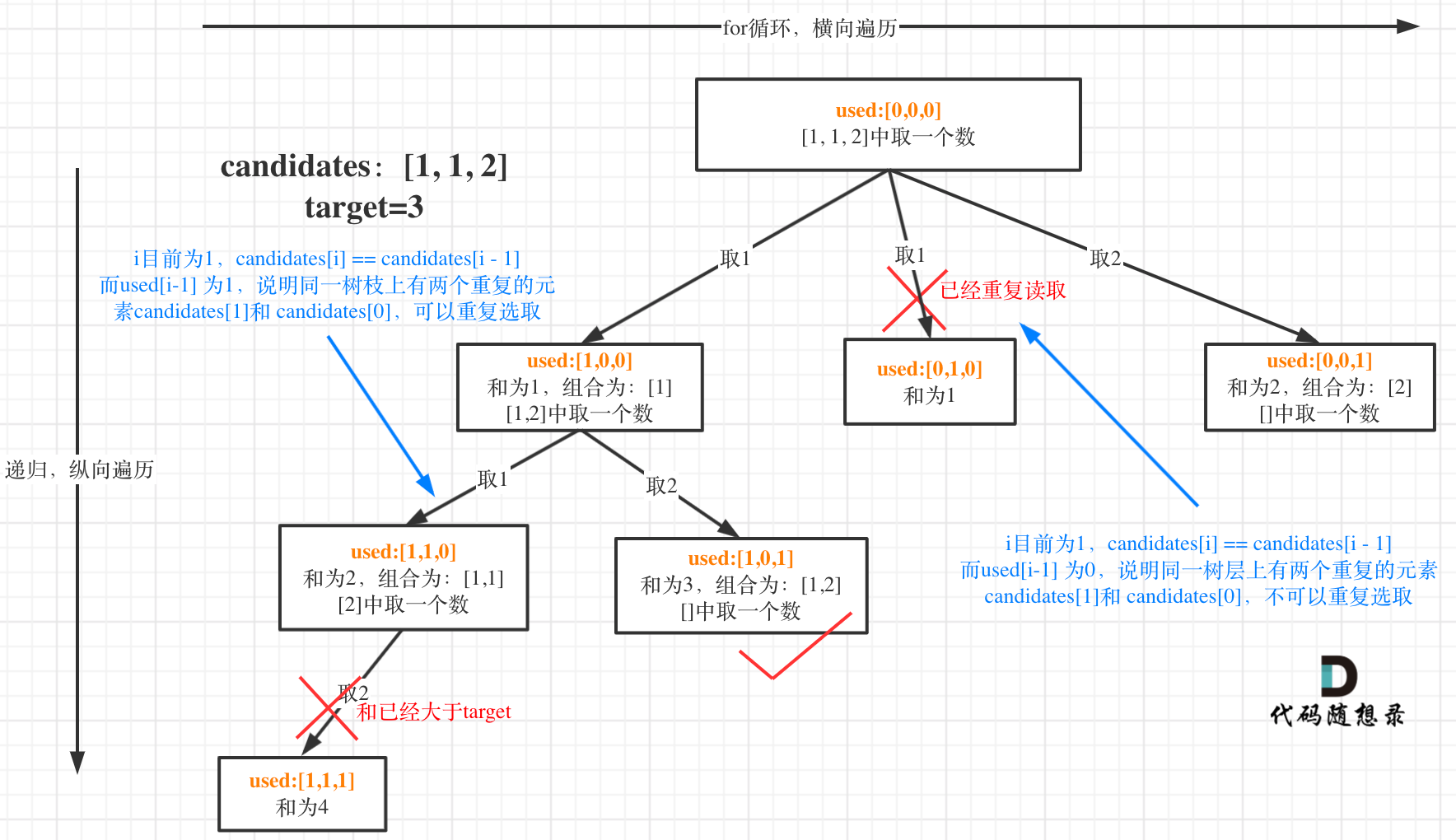
40.组合总和II1

这个集合去重的重任就是used来完成的。

  • used[i - 1] == true，说明同一树枝candidates[i - 1]使用过
  • used[i - 1] == false，说明同一树层candidates[i - 1]使用过
var combinationSum2 = function(candidates, target) {
    const res = []; path = [], len = candidates.length;
    candidates.sort((a,b)=>a-b);
    backtracking(0, 0);
    return res;
    function backtracking(sum, i) {
        if (sum === target) {
            res.push(Array.from(path));
            return;
        }
        for(let j = i; j < len; j++) {
            const n = candidates[j];
            if(j > i && candidates[j] === candidates[j-1]){
              //若当前元素和前一个元素相等
              //则本次循环结束，防止出现重复组合
              continue;
            }
            //如果当前元素值大于目标值-总和的值
            //由于数组已排序，那么该元素之后的元素必定不满足条件
            //直接终止当前层的递归
            if(n > target - sum) break;
            path.push(n);
            sum += n;
            backtracking(sum, j + 1);
            path.pop();
            sum -= n;
        }
    }
};

使用used数组去重

var combinationSum2 = function(candidates, target) {
    let res = [];
    let path = [];
    let total = 0;
    const len = candidates.length;
    candidates.sort((a, b) => a - b);
    let used = new Array(len).fill(false);
    const backtracking = (startIndex) => {
        if (total === target) {
            res.push([...path]);
            return;
        }
        for(let i = startIndex; i < len && total < target; i++) {
            const cur = candidates[i];
            if (cur > target - total || (i > 0 && cur === candidates[i - 1] && !used[i - 1])) continue;
            path.push(cur);
            total += cur;
            used[i] = true;
            backtracking(i + 1);
            path.pop();
            total -= cur;
            used[i] = false;
        }
    }
    backtracking(0);
    return res;
};

使用set

function combinationSum2(candidates, target) {
    candidates.sort((a, b) => a - b);
    const resArr = [];
    backTracking(candidates, target, 0, 0, []);
    return resArr;
    function backTracking( candidates, target, curSum, startIndex, route ) {
        if (curSum > target) return;
        if (curSum === target) {
            resArr.push([...route]);
            return;
        }
        const helperSet = new Set();
        for (let i = startIndex, length = candidates.length; i < length; i++) {
            let tempVal = candidates[i];
            if (helperSet.has(tempVal)) continue;
            helperSet.add(tempVal);
            route.push(tempVal);
            backTracking(candidates, target, curSum + tempVal, i + 1, route);
            route.pop();
        }
    }
};

131.分割回文串​

131. 分割回文串

给你一个字符串 s，请你将 s 分割成一些子串，使每个子串都是 回文串 。返回 s 所有可能的分割方案。

回文串 是正着读和反着读都一样的字符串。

示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]

对于字符串abcdef：

  • 组合问题：选取一个a之后，在bcdef中再去选取第二个，选取b之后在cdef中在选组第三个.....。
  • 切割问题：切割一个a之后，在bcdef中再去切割第二段，切割b之后在cdef中在切割第三段.....

131.分割回文串

递归用来纵向遍历，for循环用来横向遍历，切割线（就是图中的红线）切割到字符串的结尾位置，说明找到了一个切割方法。

const isPalindrome = (s, l, r) => {
    for (let i = l, j = r; i < j; i++, j--) {
        if(s[i] !== s[j]) return false;
    }
    return true;
}

var partition = function(s) {
    const res = [], path = [], len = s.length;
    backtracking(0);
    return res;
    function backtracking(i) {
        if(i >= len) {
            res.push(Array.from(path));
            return;
        }
        for(let j = i; j < len; j++) {
            if(!isPalindrome(s, i, j)) continue;
            path.push(s.slice(i, j + 1));
            backtracking(j + 1);
            path.pop();
        }
    }
};

93.复原IP地址​

93. 复原 IP 地址

有效 IP 地址 正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是 无效 IP 地址。 给定一个只包含数字的字符串 s ，用以表示一个 IP 地址，返回所有可能的有效 IP 地址，这些地址可以通过在 s 中插入 '.' 来形成。你 不能 重新排序或删除 s 中的任何数字。你可以按 任何 顺序返回答案。

  • 输入：s = "25525511135"
  • 输出：["255.255.11.135","255.255.111.35"]
var restoreIpAddresses = function (s) {
        const res=[],path=[];
        backtracking(0,0)
        return res;
        function backtracking(i){
            const len=path.length;
            if(len>4) return
            if(len===4&&i===s.length){
                res.push(path.join("."));
                return
            }
            for(let j=i;j<s.length;j++){
                const str=s.substr(i,j-i+1)
                if(str.length>3||+str>255) break;
                if(str.length>1&&str[0]==='0') break;
                path.push(str)
                backtracking(j+1)
                path.pop()
            }
        }

}

78.子集​

78. 子集

给你一个整数数组 nums ，数组中的元素 互不相同 。返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。

示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

如果把 子集问题、组合问题、分割问题都抽象为一棵树的话，那么组合问题和分割问题都是收集树的叶子节点，而子集问题是找树的所有节点！

其实子集也是一种组合问题，因为它的集合是无序的，子集{1,2} 和 子集{2,1}是一样的。

那么既然是无序，取过的元素不会重复取，写回溯算法的时候，for就要从startIndex开始，而不是从0开始！

78.子集

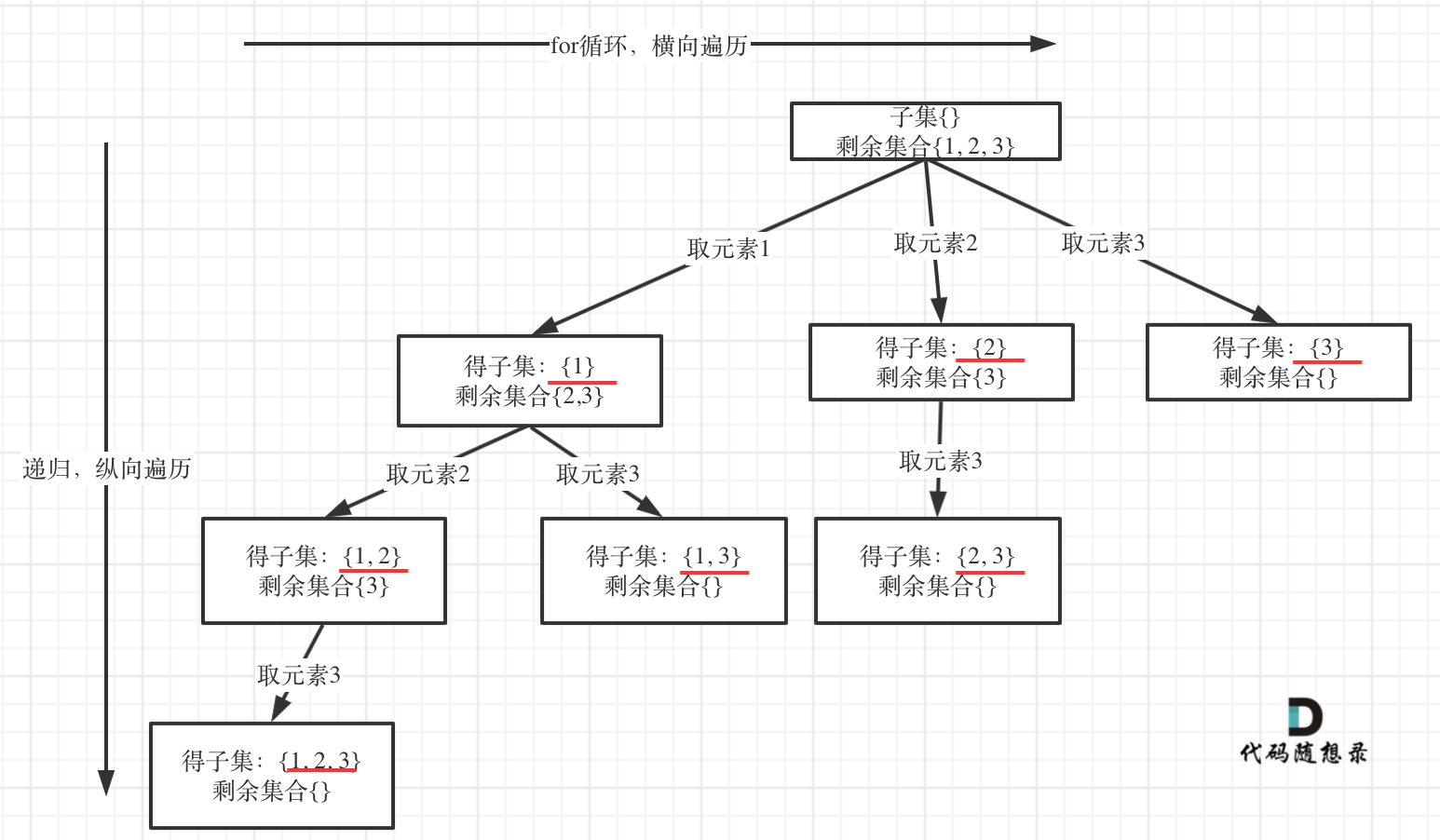
从图中红线部分，可以看出遍历这个树的时候，把所有节点都记录下来，就是要求的子集集合

var subsets = function(nums) {
    let result = []
    let path = []
    function backtracking(startIndex) {
        result.push([...path])
        for(let i = startIndex; i < nums.length; i++) {
            path.push(nums[i])// 子集收集元素
            backtracking(i + 1)// 注意从i+1开始，元素不重复取
            path.pop()// 回溯
        }
    }
    backtracking(0)
    return result
};

90.子集II​

90. 子集 II

给你一个整数数组 nums ，其中可能包含重复元素，请你返回该数组所有可能的子集（幂集）。

解集 不能 包含重复的子集。返回的解集中，子集可以按 任意顺序 排列。

  • 输入: [1,2,2]
  • 输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

这道题目和78.子集区别就是集合里有重复元素了，而且求取的子集要去重

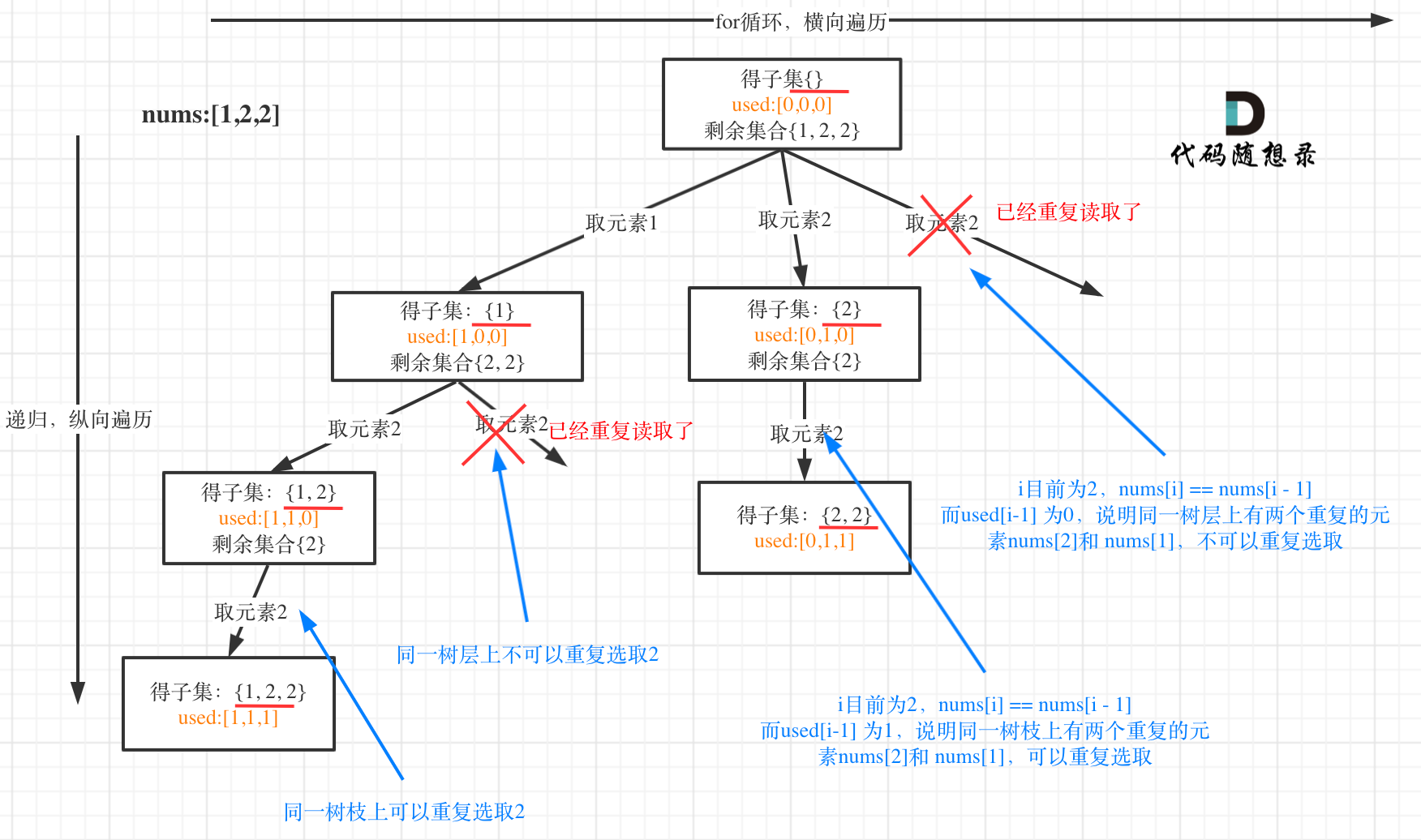
90.子集II

var subsetsWithDup = function(nums) {
    let result = []
    let path = []
    let sortNums = nums.sort((a, b) => {
        return a - b
    })
    function backtracing(startIndex, sortNums) {
        result.push([...path])
        if(startIndex > nums.length - 1) {
            return
        }
        for(let i = startIndex; i < nums.length; i++) {
            if(i > startIndex && nums[i] === nums[i - 1]) {
                continue
            }
            path.push(nums[i])
            backtracing(i + 1, sortNums)
            path.pop()
        }
    }
    backtracing(0, sortNums)
    return result
};

使用set

function subsetsWithDup(nums) {
    nums.sort((a, b) => a - b);
    const resArr = [];
    backTraking(nums, 0, []);
    return resArr;
    function backTraking(nums, startIndex, route) {
        resArr.push([...route]);
        const helperSet = new Set();
        for (let i = startIndex, length = nums.length; i < length; i++) {
            if (helperSet.has(nums[i])) continue;
            helperSet.add(nums[i]);
            route.push(nums[i]);
            backTraking(nums, i + 1, route);
            route.pop();
        }
    }
};

491.递增子序列​

491. 递增子序列

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

  • 输入: [4, 6, 7, 7]
  • 输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

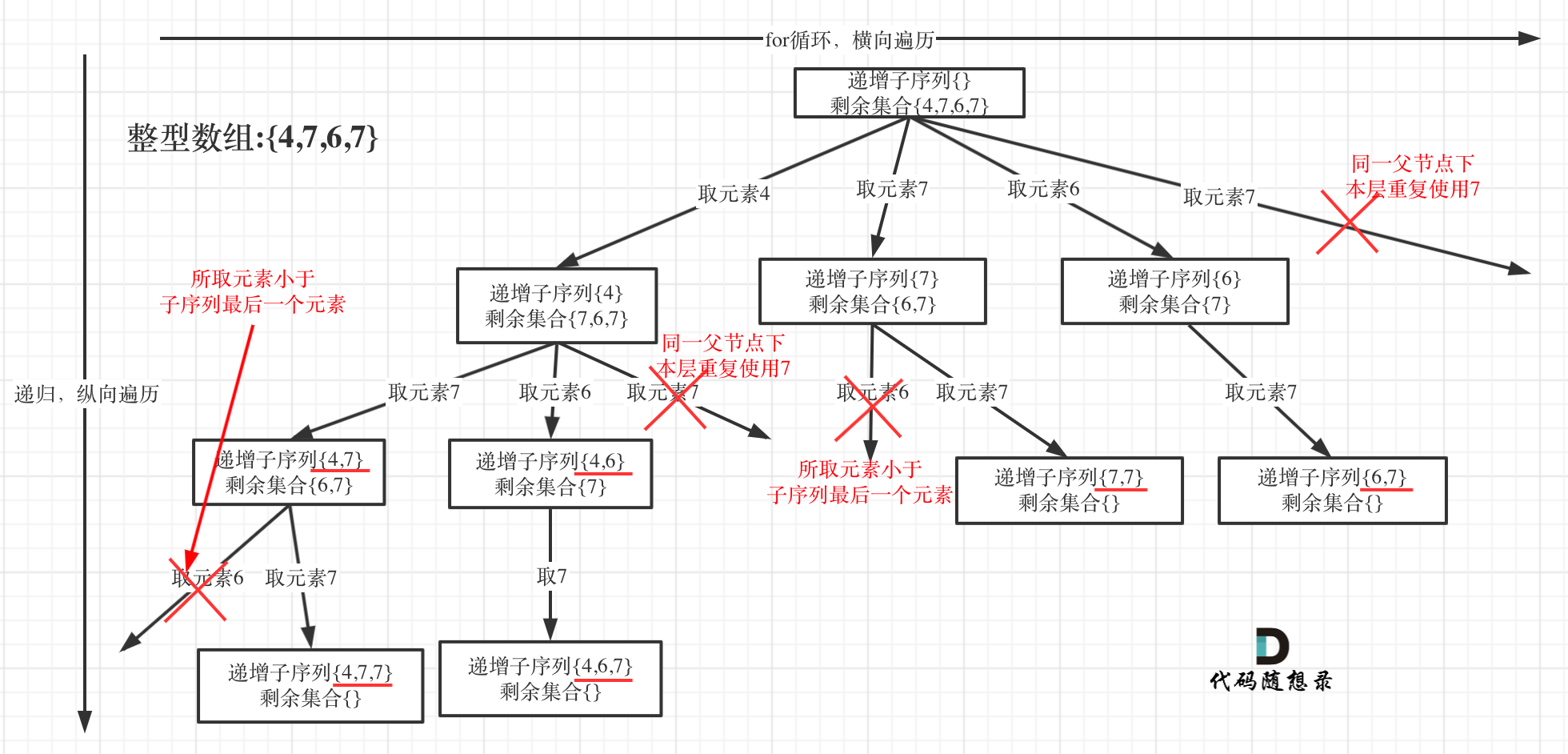
491. 递增子序列1

同一父节点下的同层上使用过的元素就不能在使用了

数值范围[-100,100]，所以完全可以用数组来做哈希。

var findSubsequences = function(nums) {
    let result = []
    let path = []
    function backtracing(startIndex) {
        if(path.length > 1) {
            result.push(path.slice())
        }
        let uset = []
        for(let i = startIndex; i < nums.length; i++) {
            if((path.length > 0 && nums[i] < path[path.length - 1]) || uset[nums[i] + 100]) {
                continue
            }
            uset[nums[i] + 100] = true
            path.push(nums[i])
            backtracing(i + 1)
            path.pop()
        }
    }
    backtracing(0)
    return result
};

用set

const findSubsequences = (nums) => {
  const res = [];
  const len = nums.length;
  const set = new Set();
  
  const dfs = (start, path) => {
    if (path.length >= 2) {
      const str = path.toString(); // path数组 转成字符串
      if (!set.has(str)) {         // set中没有存有当前path
        res.push(path.slice());    // 推入一份path的拷贝
        set.add(str);              // 存入set，记录一下
      }
    }
    for (let i = start; i < len; i++) {      // 枚举出当前所有的选项，从start到末尾
      const prev = path[path.length - 1];    // 上一个选择，即path数组的末尾元素
      const cur = nums[i];                   // 当前选择
      if (path.length == 0 || prev <= cur) { // 如果path为空，或满足递增关系，则可选择
        path.push(cur);                      // 选择当前的数字
        dfs(i + 1, path);                    // 继续往下递归，注意传的是i+1
        path.pop();                          // 撤销选择当前数字，选择别的数字
      }
    }
  };
  dfs(0, []); //递归的入口，从下标0到末尾的数组中选择合适的数加入path，组成解集。初始path是空数组
  return res;
};

优化

const findSubsequences = (nums) => {
  const res = [];
  const len = nums.length;

  const dfs = (start, path) => {
    if (start == len) {    // 递归的出口，指针已经越界
      if (path.length >= 2) {   // path长度大于等于2
        res.push(path.slice()); // 加入解集
        return;
      }
    }
    path.push(nums[start]);         // 进行选择
    for (let i = start + 1; i <= len; i++) { //枚举出选项，从start+1到len都可以选
      const prev = nums[start];     // 递归树中上一层的选择
      const cur = nums[i];          // 当前的选择
      if (i < len && cur == prev) { // i还没越界，且当前选择和上一层的选择相同
        dfs(i, path);               // 递归完当前选择，就break，避免i自增，导致i==len
        break;                      // 从而避免导致执行else if里的逻辑，导致start==len
                                    // 导致来递归的出口，path推入res
      } else if (i == len || prev < cur) { // i==len越界，让它落入递归，在递归的出口中return
        dfs(i, path);                      // 或prev < cur，满足条件，往下递归
      }
    }
    path.pop();                     // 撤销选择
  };
  for (let i = 0; i < len; i++) {
    dfs(i, []);
  }
  return res;
};

46. 全排列​

46. 全排列

给定一个 没有重复 数字的序列，返回其所有可能的全排列。

示例:

  • 输入: [1,2,3]
  • 输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]
var permute = function(nums) {
    const res=[],path=[];
    backtracking(nums,nums.length,[]);
    return res;
    
    function backtracking(n,k,used){
        if(path.length===k){
            res.push(Array.from(path));
            return ;
        }
        for(let i=0;i<k;i++){
            if(used[i]) continue;
            path.push(n[i]);
            used[i]=true;
            backtracking(n,k,used);
            path.pop();
            used[i]=false;
        }
    }
};

47.全排列 II​

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

  • 输入：nums = [1,2,3]
  • 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

这道题目和46.全排列的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

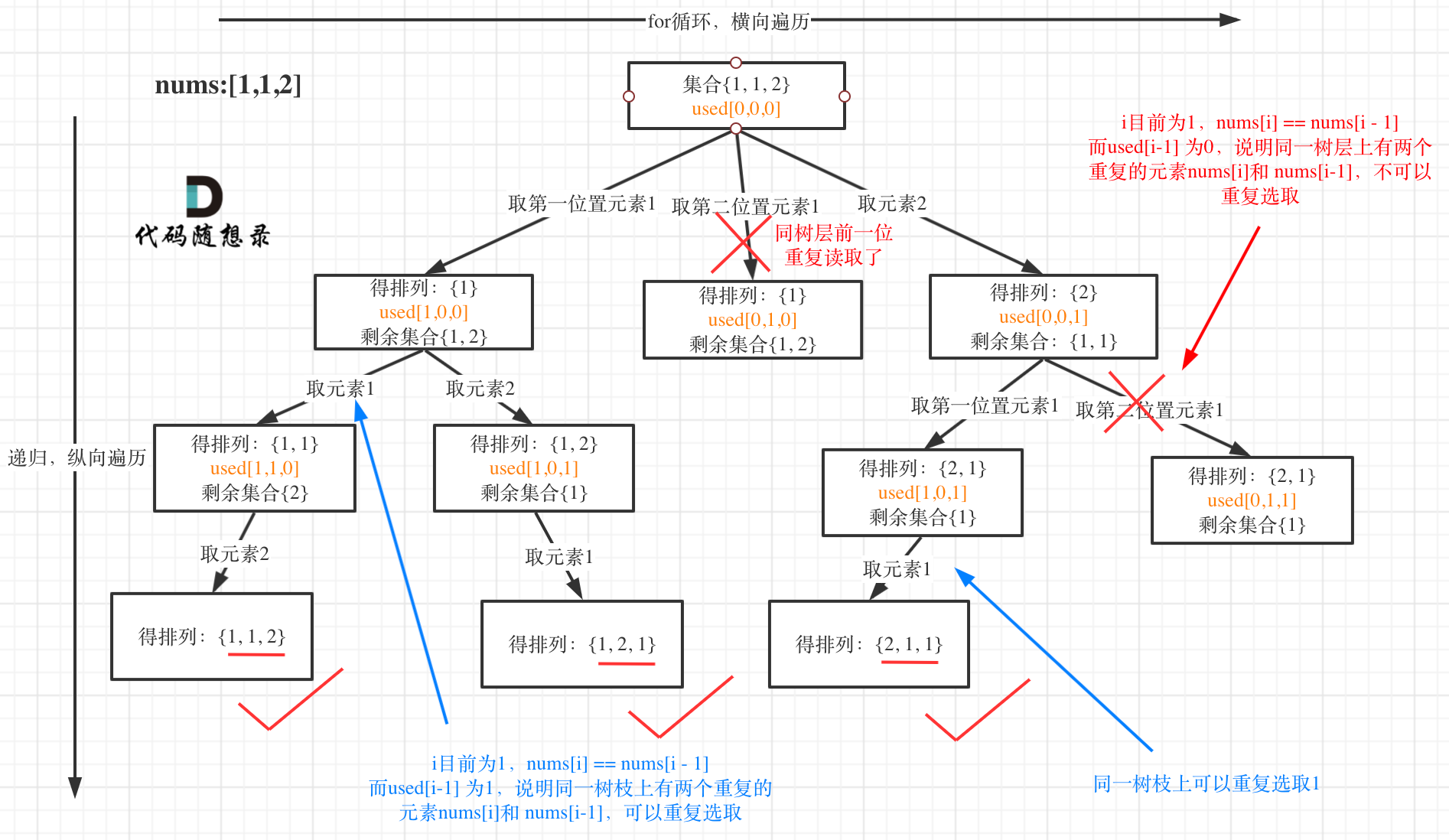
47.全排列II1

一般来说：组合问题和排列问题是在树形结构的叶子节点上收集结果，而子集问题就是取树上所有节点的结果。

var permuteUnique = function (nums) {
    nums.sort((a, b) => {
        return a - b
    })
    let result = []
    let path = []

    function backtracing( used) {
        if (path.length === nums.length) {
            result.push([...path])
            return
        }
        for (let i = 0; i < nums.length; i++) {
            if (i > 0 && nums[i] === nums[i - 1] && !used[i - 1]) {
                continue
            }
            if (!used[i]) {
                used[i] = true
                path.push(nums[i])
                backtracing(used)
                path.pop()
                used[i] = false
            }


        }
    }
    backtracing([])
    return result
};

二维数组全排列​

记录一下（dfs算法，无回溯）

思想：主要是排列index数组的变化，根据对应的数组长度取不同的下标值，可通过画树，明白其过程。–每次都从第一个位置开始

     let res = [];
            let len = arr.length;
            let index = []; //暂存可能排列的情况

            sort(-1);
            function sort(start) {
                start ++;
                if(start > len - 1) {
                    return;
                }

                for(index[start] = 0; index[start] < arr[start].length; index[start] ++) {
                    sort(start);
                    if(start == len - 1) {
                        let temp = [];
                        let ss = '';
                        for(let i = len - 1; i >= 0; i --) {
                            ss += arr[start - i][index[start - i]];
                        }
                        res.push(ss);
                    }
                }     
            }
            console.log(res, '222')
            return res;

        }

        let aa = [['a','b'],['c','d'],['e','f']]
        full_arr(aa);
```

332.重新安排行程​

332. 重新安排行程

给你一份航线列表 tickets ，其中 tickets[i] = [fromi, toi] 表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。

所有这些机票都属于一个从 JFK（肯尼迪国际机场）出发的先生，所以该行程必须从 JFK 开始。如果存在多种有效的行程，请你按字典排序返回最小的行程组合。

例如，行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小，排序更靠前。 假定所有机票至少存在一种合理的行程。且所有的机票 必须都用一次 且 只能用一次。

回溯，出现合适结果马上退出的方法： 1、思路改变：每层dfs保留自己的map，此map表示未进行的旅程； 2、若用完车票，则返回true， 反之返回false；进行是否继续向下递归的判断，做到遇到合适的结果马上退出； 3、提前进行排序；

var findItinerary = function(tickets) {
    var map = {};
    for (var i=0; i<tickets.length; i++) {
        !map[tickets[i][0]] && (map[tickets[i][0]] = []);
        map[tickets[i][0]].push(tickets[i][1]);
    }
    for (var i in map) {
        map[i].sort();
    }

    var t = tickets.length;
    var ans = ['JFK'];

    function dfs(start, n) {
        if (n === t) {
            return true;
        }
        var nextcity = map[start];
        if (!nextcity) return false;

        for (var i=0; i<nextcity.length; i++) {
            var city = nextcity[i];
            nextcity.splice(i,1);
            ans.push(city);
            if (dfs(city, n+1)) return true;
            ans.pop();
            nextcity.splice(i,0,city);
        }
    }

    dfs('JFK', 0);
    return ans;
};

51. N 皇后​

51. N 皇后

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

var solveNQueens = function(n) {
    function isValid(row, col, chessBoard, n) {

        for(let i = 0; i < row; i++) {
            if(chessBoard[i][col] === 'Q') {
                return false
            }
        }

        for(let i = row - 1, j = col - 1; i >= 0 && j >= 0; i--, j--) {
            if(chessBoard[i][j] === 'Q') {
                return false
            }
        }

        for(let i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if(chessBoard[i][j] === 'Q') {
                return false
            }
        }
        return true
    }

    function transformChessBoard(chessBoard) {
        let chessBoardBack = []
        chessBoard.forEach(row => {
            let rowStr = ''
            row.forEach(value => {
                rowStr += value
            })
            chessBoardBack.push(rowStr)
        })

        return chessBoardBack
    }

    let result = []
    function backtracing(row,chessBoard) {
        if(row === n) {
            result.push(transformChessBoard(chessBoard))
            return
        }
        for(let col = 0; col < n; col++) {
            if(isValid(row, col, chessBoard, n)) {
                chessBoard[row][col] = 'Q'
                backtracing(row + 1,chessBoard)
                chessBoard[row][col] = '.'
            }
        }
    }
    let chessBoard = new Array(n).fill([]).map(() => new Array(n).fill('.'))
    backtracing(0,chessBoard)
    return result
    
};

37. 解数独​

37. 解数独

编写一个程序，通过填充空格来解决数独问题。

数独的解法需 遵循如下规则：

数字 1-9 在每一行只能出现一次。 数字 1-9 在每一列只能出现一次。 数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。（请参考示例图） 数独部分空格内已填入了数字，空白格用 '.' 表示。

  • 输入：[["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
  • 输出：["JFK", "MUC", "LHR", "SFO", "SJC"]

本题中棋盘的每一个位置都要放一个数字，并检查数字是否合法，解数独的树形结构要比N皇后更宽更深。

判断棋盘是否合法有如下三个维度：

  • 同行是否重复
  • 同列是否重复
  • 9宫格里是否重复
var solveSudoku = function(board) {
    function isValid(row, col, val, board) {
        let len = board.length
        // 行不能重复
        for(let i = 0; i < len; i++) {
            if(board[row][i] === val) {
                return false
            }
        }
        // 列不能重复
        for(let i = 0; i < len; i++) {
            if(board[i][col] === val) {
                return false
            }
        }
        let startRow = Math.floor(row / 3) * 3
        let startCol = Math.floor(col / 3) * 3

        for(let i = startRow; i < startRow + 3; i++) {
            for(let j = startCol; j < startCol + 3; j++) {
                if(board[i][j] === val) {
                    return false
                }
            }
        }

        return true
    }

    function backTracking() {
        for(let i = 0; i < board.length; i++) {
            for(let j = 0; j < board[0].length; j++) {
                if(board[i][j] !== '.') continue
                for(let val = 1; val <= 9; val++) {
                    if(isValid(i, j, `${val}`, board)) {
                        board[i][j] = `${val}`
                        if (backTracking()) {
                            return true
                        }
                        
                        board[i][j] = `.`
                    }
                }
                return false
            }
        }
        return true
    }
    backTracking(board)
    return board
    
};

贪心​

455.分发饼干​

455.分发饼干

假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。

对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j] 。如果 s[j] >= g[i]，我们可以将这个饼干 j 分配给孩子 i ，这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子，并输出这个最大数值。

示例 1:

  • 输入: g = [1,2,3], s = [1,1]
  • 输出: 1 解释:你有三个孩子和两块小饼干，3个孩子的胃口值分别是：1,2,3。虽然你有两块小饼干，由于他们的尺寸都是1，你只能让胃口值是1的孩子满足。所以你应该输出1。
var findContentChildren = function (g, s) {
    g = g.sort((a, b) => a - b)
    s = s.sort((a, b) => a - b)
    let result = 0
    let index = s.length - 1
    for (let i = g.length - 1; i >= 0; i--) {
        if (index >= 0 && s[index] >= g[i]) {
            result++
            index--
        }
    }
    return result
};

376. 摆动序列​

376. 摆动序列

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第一个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第一个序列是因为它的前两个差值都是正数，第二个序列是因为它的最后一个差值为零。

给定一个整数序列，返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些（也可以不删除）元素来获得子序列，剩下的元素保持其原始顺序。

示例 1:

  • 输入: [1,7,4,9,2,5]
  • 输出: 6
  • 解释: 整个序列均为摆动序列。

局部最优：删除单调坡度上的节点（不包括单调坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从而达到最长摆动序列。

var wiggleMaxLength = function(nums) {
    if(nums.length <= 1) return nums.length
    let result = 1
    let preDiff = 0
    let curDiff = 0
    for(let i = 0; i < nums.length - 1; i++) {
        curDiff = nums[i + 1] - nums[i]
        if((curDiff > 0 && preDiff <= 0) || (curDiff < 0 && preDiff >= 0)) {
            result++
            preDiff = curDiff
        }
    }
    return result
};

动态规划

var wiggleMaxLength = function(nums) {
    if (nums.length === 1) return 1; 
    // 考虑前i个数，当第i个值作为峰谷时的情况（则第i-1是峰顶）
    let down = 1;
    // 考虑前i个数，当第i个值作为峰顶时的情况（则第i-1是峰谷）
    let up = 1;
    for (let i = 1; i < nums.length; i++) {
        if (nums[i] < nums[i - 1]) {
            down = Math.max(up + 1, down);
        }
        if (nums[i] > nums[i - 1]) {
            up = Math.max(down + 1, up)
        }
    }
    return Math.max(down, up);
};

53. 最大子序和​

53. 最大子序和

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例: 输入: [-2,1,-3,4,-1,2,1,-5,4] 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

局部最优：当前“连续和”为负数的时候立刻放弃，从下一个元素重新计算“连续和”，因为负数加上下一个元素 “连续和”只会越来越小。

全局最优：选取最大“连续和”

局部最优的情况下，并记录最大的“连续和”，可以推出全局最优。

从代码角度上来讲：遍历nums，从头开始用count累积，如果count一旦加上nums[i]变为负数，那么就应该从nums[i+1]开始从0累积count了，因为已经变为负数的count，只会拖累总和。

这相当于是暴力解法中的不断调整最大子序和区间的起始位置。

var maxSubArray = function(nums) {
    let result = -Infinity
    let count = 0
    for(let i = 0; i < nums.length; i++) {
        count += nums[i]
        if(count > result) {
            result = count
        }
        if(count < 0) {
            count = 0
        }
    }
    return result
};

55. 跳跃游戏​

55. 跳跃游戏

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

判断你是否能够到达最后一个位置。

示例 1:

  • 输入: [2,3,1,1,4]
  • 输出: true
  • 解释: 我们可以先跳 1 步，从位置 0 到达 位置 1, 然后再从位置 1 跳 3 步到达最后一个位置。
var canJump = function(nums) {
    if(nums.length === 1) return true
    let cover = 0
    for(let i = 0; i <= cover; i++) {
        cover = Math.max(cover, i + nums[i])
        if(cover >= nums.length - 1) {
            return true
        }
    }
    return false
};

45.跳跃游戏II​

45.跳跃游戏II

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

  • 输入: [2,3,1,1,4]
  • 输出: 2
  • 解释: 跳到最后一个位置的最小跳跃数是 2。从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明: 假设你总是可以到达数组的最后一个位置。

var jump = function(nums) {
    let curIndex = 0
    let nextIndex = 0
    let steps = 0
    for(let i = 0; i < nums.length - 1; i++) {
        nextIndex = Math.max(nums[i] + i, nextIndex)
        if(i === curIndex) {
            curIndex = nextIndex
            steps++
        }
    }
    return steps
};

1005. K次取反后最大化的数组和​

1005.K次取反后最大化的数组和

给定一个整数数组 A，我们只能用以下方法修改该数组：我们选择某个索引 i 并将 A[i] 替换为 -A[i]，然后总共重复这个过程 K 次。（我们可以多次选择同一个索引 i。）

以这种方式修改数组后，返回数组可能的最大和。

示例 1：

  • 输入：A = [4,2,3], K = 1
  • 输出：5
  • 解释：选择索引 (1,) ，然后 A 变为 [4,-2,3]。

示例 2：

  • 输入：A = [3,-1,0,2], K = 3
  • 输出：6
  • 解释：选择索引 (1, 2, 2) ，然后 A 变为 [3,1,0,2]。

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。

局部最优可以推出全局最优。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让 数组和 达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比 反转5得到的-5 大多了），全局最优：整个 数组和 达到最大。

  • 第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
  • 第二步：从前向后遍历，遇到负数将其变为正数，同时K--
  • 第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
  • 第四步：求和
var largestSumAfterKNegations = function(nums, k) {
    nums.sort((a, b) => {
        return Math.abs(b) - Math.abs(a)
    })
    for(let i = 0; i < nums.length; i++) {
        if(nums[i] < 0 && k > 0) {
            nums[i] *= -1
            k--
        }
    }

    if(k > 0 && k % 2 === 1) {
        nums[nums.length - 1] *= -1   
    }
    k = 0

    return nums.reduce((a, b) => {
        return a + b
    })
};

优化 一次遍历

var largestSumAfterKNegations = function(nums, k) {
    nums.sort((a, b) => Math.abs(b) - Math.abs(a)); // 排序
    let sum = 0;
    for(let i = 0; i < nums.length; i++) {
        if(nums[i] < 0 && k-- > 0) { // 负数取反（k 数量足够时）
            nums[i] = -nums[i];
        }
        sum += nums[i]; // 求和
    }
    if(k % 2 > 0) { // k 有多余的（k若消耗完则应为 -1）
        sum -= 2 * nums[nums.length - 1]; // 减去两倍的最小值（因为之前加过一次）
    }
    return sum;
};

134. 加油站​

134. 加油站

在一条环路上有 N 个加油站，其中第 i 个加油站有汽油 gas[i] 升。

你有一辆油箱容量无限的的汽车，从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发，开始时油箱为空。

如果你可以绕环路行驶一周，则返回出发时加油站的编号，否则返回 -1。

说明:

  • 如果题目有解，该答案即为唯一答案。
  • 输入数组均为非空数组，且长度相同。
  • 输入数组中的元素均为非负数。

示例 1: 输入:

  • gas = [1,2,3,4,5]
  • cost = [3,4,5,1,2]

输出: 3 解释:

  • 从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
  • 开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
  • 开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
  • 开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
  • 开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
  • 开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
  • 因此，3 可为起始索引。

暴力

var canCompleteCircuit = function(gas, cost) {
    for(let i = 0; i < cost.length; i++) {
        let rest = gas[i] - cost[i]  //记录剩余油量
        // 以i为起点行驶一圈，index为下一个目的地
        let index = (i + 1) % cost.length
        while(rest > 0 && index !== i) {
            rest += gas[index] - cost[index]
            index = (index + 1) % cost.length
        }
        if(rest >= 0 && index === i) return i
    }
    return -1
};

优化一

var canCompleteCircuit = function(gas, cost) {
    let curSum = 0
    let min = Infinity
    for(let i = 0; i < gas.length; i++) {
        let rest = gas[i] - cost[i]
        curSum += rest
        if(curSum < min) {
            min = curSum
        }
    }
    if(curSum < 0) return -1   //1.总油量 小于 总消耗量
    if(min >= 0) return 0      //2. 说明油箱里油没断过
                               //3. 从后向前，看哪个节点能这个负数填平，能把这个负数填平的节点就是出发节点
    for(let i = gas.length -1; i >= 0; i--) {
        let rest = gas[i] - cost[i]
        min += rest
        if(min >= 0) {
            return i
        }
    }
    return -1
}

优化二

var canCompleteCircuit = function(gas, cost) {
    const gasLen = gas.length
    let start = 0
    let curSum = 0
    let totalSum = 0

    for(let i = 0; i < gasLen; i++) {
        curSum += gas[i] - cost[i]
        totalSum += gas[i] - cost[i]
        if(curSum < 0) {
            curSum = 0
            start = i + 1
        }
    }

    if(totalSum < 0) return -1

    return start
};

135. 分发糖果​

135. 分发糖果

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

  • 每个孩子至少分配到 1 个糖果。
  • 相邻的孩子中，评分高的孩子必须获得更多的糖果。

那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1:

  • 输入: [1,0,2]
  • 输出: 5
  • 解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。

示例 2:

  • 输入: [1,2,2]
  • 输出: 4
  • 解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

两次贪心的策略：

  • 一次是从左到右遍历，只比较右边孩子评分比左边大的情况。
  • 一次是从右到左遍历，只比较左边孩子评分比右边大的情况。
var candy = function(ratings) {
    let candys = new Array(ratings.length).fill(1)

    for(let i = 1; i < ratings.length; i++) {
        if(ratings[i] > ratings[i - 1]) {
            candys[i] = candys[i - 1] + 1
        }
    }

    for(let i = ratings.length - 2; i >= 0; i--) {
        if(ratings[i] > ratings[i + 1]) {
            candys[i] = Math.max(candys[i], candys[i + 1] + 1)
        }
    }

    let count = candys.reduce((a, b) => {
        return a + b
    })

    return count
};

860.柠檬水找零​

860.柠檬水找零

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。

顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

示例 1：

  • 输入：[5,5,5,10,20]
  • 输出：true
  • 解释：
    • 前 3 位顾客那里，我们按顺序收取 3 张 5 美元的钞票。
    • 第 4 位顾客那里，我们收取一张 10 美元的钞票，并返还 5 美元。
    • 第 5 位顾客那里，我们找还一张 10 美元的钞票和一张 5 美元的钞票。
    • 由于所有客户都得到了正确的找零，所以我们输出 true。

只需要维护三种金额的数量，5，10和20。

有如下三种情况：

  • 情况一：账单是5，直接收下。
  • 情况二：账单是10，消耗一个5，增加一个10
  • 情况三：账单是20，优先消耗一个10和一个5，如果不够，再消耗三个5
var lemonadeChange = function(bills) {
    let fiveCount = 0
    let tenCount = 0

    for(let i = 0; i < bills.length; i++) {
        let bill = bills[i]
        if(bill === 5) {
            fiveCount += 1
        } else if (bill === 10) {
            if(fiveCount > 0) {
                fiveCount -=1
                tenCount += 1
            } else {
                return false
            }
        } else {
            if(tenCount > 0 && fiveCount > 0) {
                tenCount -= 1
                fiveCount -= 1 
            } else if(fiveCount >= 3) {
                fiveCount -= 3
            } else {
                return false
            }
        } 
    }
    return true
};

406.根据身高重建队列​

406.根据身高重建队列

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

示例 1：

  • 输入：people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
  • 输出：[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
  • 解释：
    • 编号为 0 的人身高为 5 ，没有身高更高或者相同的人排在他前面。
    • 编号为 1 的人身高为 7 ，没有身高更高或者相同的人排在他前面。
    • 编号为 2 的人身高为 5 ，有 2 个身高更高或者相同的人排在他前面，即编号为 0 和 1 的人。
    • 编号为 3 的人身高为 6 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
    • 编号为 4 的人身高为 4 ，有 4 个身高更高或者相同的人排在他前面，即编号为 0、1、2、3 的人。
    • 编号为 5 的人身高为 7 ，有 1 个身高更高或者相同的人排在他前面，即编号为 1 的人。
    • 因此 [[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]] 是重新构造后的队列。

按照身高排序之后，优先按身高高的people的k来插入，后序插入节点也不会影响前面已经插入的节点，最终按照k的规则完成了队列。

所以在按照身高从大到小排序后：

局部最优：优先按身高高的people的k来插入。插入操作过后的people满足队列属性

全局最优：最后都做完插入操作，整个队列满足题目队列属性

var reconstructQueue = function(people) {
    let queue = []
    people.sort((a, b ) => {
        if(b[0] !== a[0]) {
            return b[0] - a[0]
        } else {
            return a[1] - b[1]
        }
        
    })

    for(let i = 0; i < people.length; i++) {
        queue.splice(people[i][1], 0, people[i])
    }
    return queue
};

452. 用最少数量的箭引爆气球​

452. 用最少数量的箭引爆气球

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以纵坐标并不重要，因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。

一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

给你一个数组 points ，其中 points [i] = [xstart,xend] ，返回引爆所有气球所必须射出的最小弓箭数。

示例 1：

  • 输入：points = [[10,16],[2,8],[1,6],[7,12]]
  • 输出：2
  • 解释：对于该样例，x = 6 可以射爆 [2,8],[1,6] 两个气球，以及 x = 11 射爆另外两个气球

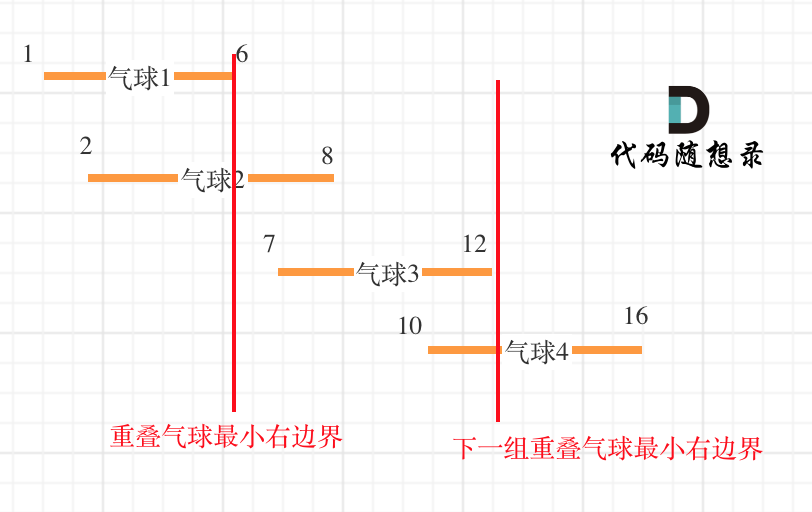
452.用最少数量的箭引爆气球

var findMinArrowShots = function(points) {
    points.sort((a, b) => {
        return a[0] - b[0]
    })
    let result = 1
    for(let i = 1; i < points.length; i++) {
        if(points[i][0] > points[i - 1][1]) {
            result++
        } else {
            points[i][1] = Math.min(points[i - 1][1], points[i][1])
        }
    }

    return result
};

435. 无重叠区间​

435. 无重叠区间

给定一个区间的集合，找到需要移除区间的最小数量，使剩余区间互不重叠。

注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”，但没有相互重叠。

示例 1:

  • 输入: [ [1,2], [2,3], [3,4], [1,3] ]
  • 输出: 1
  • 解释: 移除 [1,3] 后，剩下的区间没有重叠。

示例 2:

  • 输入: [ [1,2], [1,2], [1,2] ]
  • 输出: 2
  • 解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。

按照右边界排序，从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。

此时问题就是要求非交叉区间的最大个数。

右边界排序之后，局部最优：优先选右边界小的区间，所以从左向右遍历，留给下一个区间的空间大一些，从而尽量避免交叉。全局最优：选取最多的非交叉区间。

435.无重叠区间

按照右边界

var eraseOverlapIntervals = function(intervals) {
    intervals.sort((a, b) => {
        return a[1] - b[1]
    })

    let count = 1
    let end = intervals[0][1]

    for(let i = 1; i < intervals.length; i++) {
        let interval = intervals[i]
        if(interval[0] >= end) {
            end = interval[1]
            count += 1
        }
    }
    
    return intervals.length - count
};

按照左边界

var eraseOverlapIntervals = function(intervals) {
    // 按照左边界升序排列
    intervals.sort((a, b) => a[0] - b[0])
    let count = 1
    let end = intervals[intervals.length - 1][0]
    // 倒序遍历，对单个区间来说，左边界越大越好，因为给前面区间的空间越大
    for(let i = intervals.length - 2; i >= 0; i--) {
        if(intervals[i][1] <= end) {
            count++
            end = intervals[i][0]
        }
    }
    // count 记录的是最大非重复区间的个数
    return intervals.length - count
}

763.划分字母区间​

763.划分字母区间

字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段，同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。

示例：

  • 输入：S = "ababcbacadefegdehijhklij"
  • 输出：[9,7,8] 解释： 划分结果为 "ababcbaca", "defegde", "hijhklij"。 每个字母最多出现在一个片段中。 像 "ababcbacadefegde", "hijhklij" 的划分是错误的，因为划分的片段数较少。

提示：

  • S的长度在[1, 500]之间。
  • S只包含小写字母 'a' 到 'z' 。

题目要求同一字母最多出现在一个片段中，那么如何把同一个字母的都圈在同一个区间里呢？

在遍历的过程中相当于是要找每一个字母的边界，如果找到之前遍历过的所有字母的最远边界，说明这个边界就是分割点了。此时前面出现过所有字母，最远也就到这个边界了。

可以分为如下两步：

  • 统计每一个字符最后出现的位置
  • 从头遍历字符，并更新字符的最远出现下标，如果找到字符最远出现位置下标和当前下标相等了，则找到了分割点

如图：

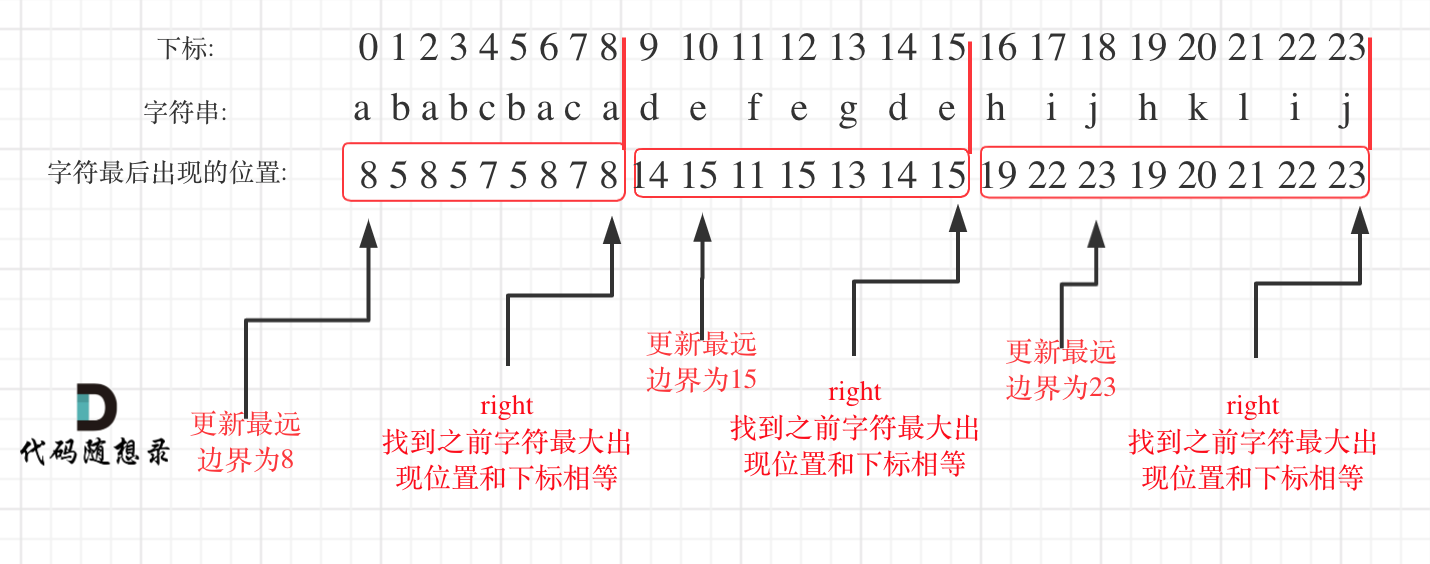
763.划分字母区间

var partitionLabels = function(s) {
    let hash = {}
    for(let i = 0; i < s.length; i++) {
        hash[s[i]] = i
    }
    let result = []
    let left = 0
    let right = 0
    for(let i = 0; i < s.length; i++) {
        right = Math.max(right, hash[s[i]])
        if(right === i) {
            result.push(right - left + 1)
            left = i + 1
        }
    }
    return result
};

56. 合并区间​

56. 合并区间

给出一个区间的集合，请合并所有重叠的区间。

示例 1:

  • 输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
  • 输出: [[1,6],[8,10],[15,18]]
  • 解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

示例 2:

  • 输入: intervals = [[1,4],[4,5]]
  • 输出: [[1,5]]
  • 解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。

按照左边界从小到大排序之后，如果 intervals[i][0] < intervals[i - 1][1] 即intervals[i]左边界 < intervals[i - 1]右边界，则一定有重复，因为intervals[i]的左边界一定是大于等于intervals[i - 1]的左边界。

即：intervals[i]的左边界在intervals[i - 1]左边界和右边界的范围内，那么一定有重复！

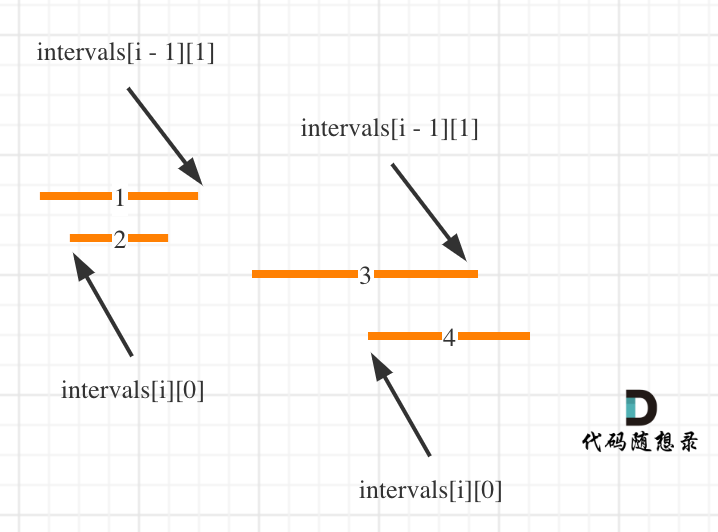
56.合并区间

用合并区间后左边界和右边界，作为一个新的区间，加入到result数组里就可以了。如果没有合并就把原区间加入到result数组。

var merge = function (intervals) {
    intervals.sort((a, b) => a[0] - b[0]);
    let prev = intervals[0]
    let result = []
    for(let i =0; i<intervals.length; i++){
        let cur = intervals[i]
        if(cur[0] > prev[1]){
            result.push(prev)
            prev = cur
        }else{
            prev[1] = Math.max(cur[1],prev[1])
        }
    }
    result.push(prev)
    return result
};

738.单调递增的数字​

738.单调递增的数字

给定一个非负整数 N，找出小于或等于 N 的最大的整数，同时这个整数需要满足其各个位数上的数字是单调递增。

（当且仅当每个相邻位数上的数字 x 和 y 满足 x <= y 时，我们称这个整数是单调递增的。）

示例 1:

  • 输入: N = 10
  • 输出: 9

示例 2:

  • 输入: N = 1234
  • 输出: 1234
var monotoneIncreasingDigits = function(n) {
    n = n.toString()
    n = n.split('').map(item => {
        return +item
    })
    let flag = Infinity
    for(let i = n.length - 1; i > 0; i--) {
        if(n [i - 1] > n[i]) {
            flag = i
            n[i - 1] = n[i - 1] - 1
            n[i] = 9
        }
    }

    for(let i = flag; i < n.length; i++) {
        n[i] = 9
    }

    n = n.join('')
    return +n
};

968.监控二叉树​

968.监控二叉树

给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

从下往上看，局部最优：让叶子节点的父节点安摄像头，所用摄像头最少，整体最优：全部摄像头数量所用最少！

可以使用后序遍历也就是左右中的顺序，这样就可以在回溯的过程中从下到上进行推导了。

节点的状态值： 0 表示无覆盖 1 表示 有摄像头 2 表示有覆盖

为了让摄像头数量最少，我们要尽量让叶子节点的父节点安装摄像头，这样才能摄像头的数量最少。

那么空节点不能是无覆盖的状态，这样叶子节点就要放摄像头了，空节点也不能是有摄像头的状态，这样叶子节点的父节点就没有必要放摄像头了，而是可以把摄像头放在叶子节点的爷爷节点上。

递归的终止条件应该是遇到了空节点

// 空节点，该节点有覆盖
if (cur == NULL) return 2;
  • 情况1：左右节点都有覆盖

左孩子有覆盖，右孩子有覆盖，那么此时中间节点应该就是无覆盖的状态了。

// 左右节点都有覆盖
if (left == 2 && right == 2) return 0;
  • 情况2：左右节点至少有一个无覆盖的情况

如果是以下情况，则中间节点（父节点）应该放摄像头：

left == 0 && right == 0 左右节点无覆盖 left == 1 && right == 0 左节点有摄像头，右节点无覆盖 left == 0 && right == 1 左节点有无覆盖，右节点摄像头 left == 0 && right == 2 左节点无覆盖，右节点覆盖 left == 2 && right == 0 左节点覆盖，右节点无覆盖

if (left == 0 || right == 0) {
    result++;
    return 1;
}

这个不难理解，毕竟有一个孩子没有覆盖，父节点就应该放摄像头。

  • 情况3：左右节点至少有一个有摄像头

如果是以下情况，其实就是 左右孩子节点有一个有摄像头了，那么其父节点就应该是2（覆盖的状态）

left == 1 && right == 2 左节点有摄像头，右节点有覆盖 left == 2 && right == 1 左节点有覆盖，右节点有摄像头 left == 1 && right == 1 左右节点都有摄像头

if (left == 1 || right == 1) return 2;
  • 情况4：头结点没有覆盖

以上都处理完了，递归结束之后，可能头结点 还有一个无覆盖的情况，如图：

var minCameraCover = function(root) {
    let result = 0
    function traversal(cur) {
        if(cur === null) {
            return 2
        }

        let left = traversal(cur.left)
        let right = traversal(cur.right)

        if(left === 2 && right === 2) {
            return 0
        }

        if(left === 0 || right === 0) {
            result++
            return 1
        }

        if(left === 1 || right === 1) {
            return 2
        }

        return -1
    }

    if(traversal(root) === 0) {
        result++
    }

    return result
               
};

数论​

动态规划​

70. 爬楼梯​

70. 爬楼梯

var climbStairs = function (n) {
    if (n <= 1) return n;
    a = 1;
    b = 2;
    for (let i = 3; i <= n; i++) {
        sum = a + b;
        a = b;
        b = sum;
    }
    return b;
}

剑指 Offer 10- I. 斐波那契数列​

剑指 Offer 10- I. 斐波那契数列

var fib = function(n) {
    let n1 = 0, n2 = 1, sum;
    for(let i = 0; i < n; i++){
        sum = (n1 + n2) % 1000000007;
        n1 = n2;
        n2 = sum;
    }
    return n1;
};

剑指 Offer 62. 圆圈中最后剩下的数字​

剑指 Offer 62. 圆圈中最后剩下的数字

var lastRemaining = function(n, m) {
    let now = 0;
    for(let i = 2; i <= n; i++) {
        now = (now + m) % i;
    }
    return now;
};

5. 最长回文子串​

5. 最长回文子串

给你一个字符串 s，找到 s 中最长的回文子串。

var longestPalindrome = function(s) {
        let n=s.length
        let res=''
        let dp=Array.from(new Array(n),()=>new Array(n).fill(false))
        for(let i=n-1;i>=0;i--){
            for(let j=i;j<n;j++){
                dp[i][j]=s[i]===s[j]&&(j-i<2||dp[i+1][j-1])
                if(dp[i][j]&&j-i+1>res.length){
                    res=s.substring(i,j+1)
                }
            }
        }
        return res
};

647. 回文子串​

647. 回文子串

给你一个字符串 s ，请你统计并返回这个字符串中 回文子串 的数目

var countSubstrings=function(s){
    const n=s.length;
    let ans=0;
    let dp=Array.from(Array(n),()=>Array(n).fill(false))
    for(let j=0;j<n;j++){
        for(let i=0;i<=j;i++){
            if(s[i]===s[j]){
                if(j-i<2){
                    dp[i][j]=true
                }else{
                    dp[i][j]=dp[i+1][j-1]
                }
                ans+=dp[i][j]?1:0
            }
        }
    }
    return ans
}

516. 最长回文子序列​

516.最长回文子序列

var longestPalindromeSubseq=function(s){
    const n=s.length
    const dp=new Array(n).fill(0).map(()=>new Array(n).fill(0))
    for(let i=0;i<n;i++){
        dp[i][i]=1
    }
    for(let i=n-1;i>=0;i--){
        for(let j=i+1;j<n;j++){
            if(s[i]=s[j]){
                dp[i][j]=dp[i+1][j-1]+2   //如果左右端点的相等 直接通过内层状态进行转移
            }else{
                dp[i][j]=Math.max(dp[i+1][j],dp[i][j-1])  //不相等  则进行左右各选取一个进行状态结果比较
            }
        }
    }
    return dp[0][n-1]
}

300. 最长递增子序列​

300. 最长递增子序列

var lengthOfLIS = function (nums) {
  const dp = new Array(nums.length).fill(1);
  for (let i = 0; i < nums.length; i++) {
    // i与i前面的元素比较
    for (let j = 0; j < i; j++) {
      // 找比i小的元素，找到一个，就让当前序列的最长子序列长度加1
      if (nums[i] > nums[j]) {
        dp[i] = Math.max(dp[i], dp[j] + 1);
      }
    }
  }
  // 找出最大的子序列
  return Math.max(...dp);
};

718. 最长重复子数组​

718. 最长重复子数组

给两个整数数组 A 和 B ，返回两个数组中公共的、长度最长的子数组的长度。

动态规划就是要保持上一个状态和下一个状态有关系，并且是连续的。这里的子数组就相当于子串，是连续的。

这里我们初始化一个dp数组保存当前的最大连续值，dp[i][j]表示数组A的前i个元素和数组B的前j个元素组成的最长公共子数组的长度。

var findLength = function(nums1, nums2) {
        const m=nums1.length;
        const n=nums2.length;
        const dp=new Array(m+1)
        for(let i=0;i<=m;i++){
            dp[i]=new Array(n+1).fill(0)
        }
        let res=0
        for(let i=1;i<=m;i++){
            for(let j=1;j<=n;j++){
                if(nums1[i-1]===nums2[j-1]){
                    dp[i][j]=dp[i-1][j-1]+1
                }
                res=Math.max(dp[i][j],res)
            }
        }
        return res
};

1143. 最长公共子序列​

1143. 最长公共子序列

var longestCommonSubsequence=(text1,text2)=>{
    let m=text1.length,n=text2.length
    let dp=Array(m+1).fill(0).map(()=>Array(n+1).fill(0))
    for(let i=1;i<=m;i++){
        for(let j=1;j<=n;j++){
            if(text1[i-1]===text2[j-1]){
                dp[i][j]=dp[i-1][j-1]+1
            }else {
                dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1])
            }
        }
    }
    return dp[m][n]
}

1035. 不相交的线​

1035. 不相交的线

在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。

现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足：

nums1[i] == nums2[j] 且绘制的直线不与任何其他连线（非水平线）相交。 请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。

以这种方法绘制线条，并返回可以绘制的最大连线数。

本题说是求绘制的最大连线数，其实就是求两个字符串的最长公共子序列的长度！

const maxUncrossedLines = (nums1, nums2) => {
    // 两个数组长度
    const [m, n] = [nums1.length, nums2.length];
    // 创建dp数组并都初始化为0
    const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            // 根据两种情况更新dp[i][j]
            if (nums1[i - 1] === nums2[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
            }
        }
    }
    // 返回dp数组中右下角的元素
    return dp[m][n];
};

53. 最大子数组和​

53. 最大子数组和

var maxSubArray = function(nums) {
    let res = nums[0];
    let pre = 0;
    for(let num of nums) {
        pre = Math.max(pre + num, num);//maxSum[m] = Math.max(maxSum[m - 1] + nums[m])
        res = Math.max(pre, res);//确定最终最大和
    }
    return res;
};
var maxSubArray = function(nums) {
    if(nums.length === 0)return 0
    let reMax = nums[0]
    // dep[n] 代表的是第0 到 第n项之间nums所有的子项组合中的最大值
    let dep = []
    dep[0] = nums[0]
    for(let i = 1 ; i<nums.length; i++){
        // 根据排列规律 我们可以发现dep[i]其实就是
        // 当dep[i-1]>0时为dep[i-1]+nums[i]
        // 当dep[i-1]<0时就是nums[i]本身
        // 之所以是这样因为第n项的所有子项的排列规律
        // 为第n-1项的每一项加上nums[i] 再加上[nums[i]]
        // 递推规律
        // 第一个子组合是以第一个数字结尾的连续序列，也就是 [-2]，最大值-2
        // 第二个子组合是以第二个数字结尾的连续序列，也就是 [-2,1], [1]，最大值1
        // 第三个子组合是以第三个数字结尾的连续序列，也就是 [-2,1,3], [1,3], [3]，最大值4
        if(dep[i-1]>0){
            dep[i] = dep[i-1] + nums[i]
        }else{
            dep[i] = nums[i]
        }
        reMax = Math.max(reMax,dep[i])
    }
    return reMax
    
};

221. 最大正方形​

221. 最大正方形

在一个由 '0' 和 '1' 组成的二维矩阵内，找到只包含 '1' 的最大正方形，并返回其面积。

var maximalSquare = function(matrix) {
    if(!matrix||matrix.length===0||matrix[0].length===0){
      return 0
    } 
    // 1.设一个变量存放最长边
    let maxSide = 0;
    // 长宽
    let row = matrix.length;
    let column = matrix[0].length
    // 2.声明一个数组来存放每个点的最长边
    let dp=[]
    for(let i=0;i<row;i++){
        dp.push(new Array(column))
    }
    //3.遍历所有节点
    for(let i=0;i<matrix.length;i++){
        for(let j=0;j<matrix[i].length;j++){
            // 如果当前的节点等于1；
            if(matrix[i][j]=='1'){
                //且该节点的下标是0 0
                if(i==0||j==0){
                    dp[i][j]=1
                }else{  // 对应左、上、左上，三点中最小的值 + 1
                    dp[i][j]=Math.min(Math.min(dp[i-1][j],dp[i][j-1]),dp[i-1][j-1])+1
                }
            }else{
                dp[i][j]=0;
            }
          
            maxSide = Math.max(dp[i][j],maxSide)
        }
    }
    return Math.pow(maxSide,2)
};

62. 不同路径​

62. 不同路径

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish” ）。

问总共有多少条不同的路径？

var uniquePaths = function(m, n) {
    const dp=Array(m).fill().map(()=>Array(n).fill(1));
    for(let i=0;i<m;i++){
        dp[i][0]=1;
    }
    for(let i=0;i<n;i++){
        dp[0][i]=1;
    }
    for(let i=1;i<m;i++){
        for(let j=1;j<n;j++){
            //要么从左 要么从上 来继承状态
            dp[i][j]=dp[i-1][j]+dp[i][j-1];
        }
    }
    return dp[m-1][n-1];
}

63. 不同路径 II​

63. 不同路径 II

一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为 “Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为 “Finish”）。

现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径？

网格中的障碍物和空位置分别用 1 和 0 来表示。

var uniquePathsWithObstacles = function(obstacleGrid) {
    if(!obstacleGrid.length || obstacleGrid[0][0] === 1){
        return 0
    }
    const m = obstacleGrid.length, n = obstacleGrid[0].length
    const dp = new Array(m).fill(0).map(() =>  new Array(n).fill(0))

    for (let i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
        dp[i][0] = 1;
    }
    for (let j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
        dp[0][j] = 1;
    }
    for(let i = 1; i < m; i++){ 
        for(let j = 1; j < n; j++){
            if(obstacleGrid[i][j] === 0){
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
            }
        }
    }
    return dp[m - 1][n - 1]
};

状态压缩

var uniquePathsWithObstacles = function (obstacleGrid) {
    let m = obstacleGrid.length;
    let n = obstacleGrid[0].length;
    let dp = Array(n).fill(0); //用0填充，因为现在有障碍物，当前dp数组元素的值还和obstacleGrid[i][j]有关
    dp[0] = 1; //第一列 暂时用1填充
    for (let i = 0; i < m; i++) {
        for (let j = 0; j < n; j++) {
            if (obstacleGrid[i][j] == 1) {
                //注意条件，遇到障碍物dp[j]就变成0，这里包含了第一列的情况
                dp[j] = 0;
            } else if (j > 0) {
                //只有当j>0 不是第一列了才能取到j - 1
                dp[j] += dp[j - 1];
            }
        }
    }
    return dp[n - 1];
};

64. 最小路径和​

64. 最小路径和

给定一个包含非负整数的 *m* x *n* 网格 grid ，请找出一条从左上角到右下角的路径，使得路径上的数字总和为最小。

每次只能向下或者向右 —— 经典 DP 每个点只能来自上面或者左边

dp[i][j] 表示到该点的最短路径和 dp[i][j] = Math.min(dp[i - 1][j] + grid[i][j], dp[i][j - 1] + grid[i][j]) 就是第一行和第一列要初始化一下

const minPathSum = grid => {
    const [m, n] = [grid.length, grid[0].length];
    const dp = new Array(m).fill(0).map(() => new Array(n).fill(0));

    dp[0][0] = grid[0][0];
    for (let i = 1; i < m; i++) dp[i][0] = dp[i - 1][0] + grid[i][0];
    for (let j = 1; j < n; j++) dp[0][j] = dp[0][j - 1] + grid[0][j];

    for (let i = 1; i < m; i++) {
        for (let j = 1; j < n; j++) {
            dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]);
        }
    }
    return dp[m - 1][n - 1];
};

120. 三角形最小路径和​

120. 三角形最小路径和

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

const minimumTotal = (triangle) => {
    const h = triangle.length;
    // 初始化dp数组
    const dp = new Array(h);
    for (let i = 0; i < h; i++) {
        dp[i] = new Array(triangle[i].length);
    }

    for (let i = h - 1; i >= 0; i--) { // 自底而上遍历
        for (let j = 0; j < triangle[i].length; j++) { // 同一层的
            if (i == h - 1) {  // base case 最底层
                dp[i][j] = triangle[i][j];
            } else { // 状态转移方程，上一层由它下面一层计算出
                dp[i][j] = Math.min(dp[i + 1][j], dp[i + 1][j + 1]) + triangle[i][j];
            }
        }
    }
    return dp[0][0];
};

121. 买卖股票的最佳时机​

121. 买卖股票的最佳时机

限定交易次数 k=1

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润

var maxProfit = function(prices) {
    const len=prices.length
    const dp = new Array(len).fill([0,0])
      dp[0][0] = 0; // 持有现金
    dp[0][1] = -prices[0]; // 持有股票
    for (let i = 1; i < prices.length; i++){
        dp[i][0]=Math.max(dp[i-1][0],-prices[i]); //不持有股票 保持前一天现状 前一天就卖掉  或者今天卖了
        dp[i][1]=Math.max(dp[i-1][1],prices[i]+dp[i-1][0]); //持有股票 手里没钱
    }
    return dp[len-1][1]
};

状态压缩 dp[i] 只和 dp[i - 1] 有关，去掉一维

//时间复杂度O(n) 空间复杂度O(1)
const maxProfit = function (prices) {
    let n = prices.length;
    let dp = Array.from(new Array(n), () => new Array(2));
    dp[0] = 0;
    dp[1] = -prices[0];
    for (let i = 1; i < n; i++) {
        dp[0] = Math.max(dp[0], dp[1] + prices[i]);
        dp[1] = Math.max(dp[1], -prices[i]);
    }
    return dp[0];
};


const maxProfit = function (prices) {
    let n = prices.length;
    let sell = 0;
    let buy = -prices[0];
    for (let i = 1; i < n; i++) {
        sell = Math.max(sell, buy + prices[i]);
        buy = Math.max(buy, -prices[i]);
    }
    return sell;
};

贪心

var maxProfit = function (prices) {
    let lowerPrice = prices[0];// 重点是维护这个最小值（贪心的思想） 
    let profit = 0;
    for (let i = 0; i < prices.length; i++) {
        lowerPrice = Math.min(lowerPrice, prices[i]);// 贪心地选择左面的最小价格
        profit = Math.max(profit, prices[i] - lowerPrice);// 遍历一趟就可以获得最大利润
    }
    return profit;
};

122. 买卖股票的最佳时机 II​

122. 买卖股票的最佳时机 II

交易次数无限制 k = +infinity

给你一个整数数组 prices ，其中 prices[i] 表示某支股票第 i 天的价格。

在每一天，你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买，然后在 同一天 出售

状态：持有现金dp[i][0]、持有股票dp[i][1]； 如果持有现金，则可能昨天也持有现金dp[i-1][0]或者昨天持有股票并卖出，取得收益

dp[i-1][1]+prices[i]; 如果持有股票，则可能昨天也持有股票dp[i-1][1]或者昨天花掉现金，买入股票

dp[i-1][0]-prices[i];

var maxProfit = function(prices) {
    var dp = [
        []
    ];
    if(prices<1){
        return 0;
    }
    dp[0][0] = 0; // 持有现金
    dp[0][1] = -prices[0]; // 持有股票
    for (var i = 1; i < prices.length; i++) {
        if (!dp[i]) {
            dp[i] = [];
        }
        dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i])
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
    }
    return dp[prices.length - 1][0]
};

状态压缩

const maxProfit = function (prices) {
    let n = prices.length;
    let dp = Array.from(new Array(n), () => new Array(2));
    dp[0] = 0;
    dp[1] = -prices[0];
    for (let i = 1; i < n; i++) {
        dp[0] = Math.max(dp[0], dp[1] + prices[i]);
        dp[1] = Math.max(dp[1], dp[0] - prices[i]);
    }
    return dp[0];
};


//语意化
const maxProfit = function (prices) {
    let n = prices.length;
    let sell = 0;
    let buy = -prices[0];
    for (let i = 1; i < n; i++) {
        sell = Math.max(sell, buy + prices[i]);
        buy = Math.max(buy, sell - prices[i]);
    }
    return sell;
};

123. 买卖股票的最佳时机 III​

123. 买卖股票的最佳时机 III

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。

注意：你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。

var maxProfit=prices=>{
    var len=prices.length;
    var dp=Array(len+1).fill(0).map(()=>Array(5).fill(0));
    dp[0][1]=-prices[0];
    dp[0][3]=-prices[0];
    for(let i=1;i<len;i++){
        dp[i][0]=dp[i-1][0]  //不进行操作
        dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
        dp[i][2] = Math.max(dp[i - 1][2], dp[i - 1][1] + prices[i]);

        dp[i][3] = Math.max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
        dp[i][4] = Math.max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
    }
    return dp[len - 1][4];
}
const maxProfit = function (prices) {
    let buy_1 = -prices[0], sell_1 = 0
    let buy_2 = -prices[0], sell_2 = 0
    let n = prices.length
    for (let i = 1; i < n; i++) {
        sell_2 = Math.max(sell_2, buy_2 + prices[i])
        buy_2 = Math.max(buy_2, sell_1 - prices[i])
        sell_1 = Math.max(sell_1, buy_1 + prices[i])
        buy_1 = Math.max(buy_1, -prices[i])
    }
    return sell_2
}

188. 买卖股票的最佳时机 IV​

188. 买卖股票的最佳时机 IV

给定一个整数数组 prices ，它的第 i 个元素 prices[i] 是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

const maxProfit = function (k, prices) {
    let n = prices.length;
    let profit = new Array(k);//和123题一样 求出所有k的状态
    // 初始化k次交易买入卖出的利润
    for (let j = 0; j <= k; j++) {
        profit[j] = {
            buy: -prices[0],//表示有股票
            sell: 0,//表示没有股票
        };
    }
    for (let i = 0; i < n; i++) {
        for (let j = 1; j <= k; j++) {
            //122题可以交易无数次，188交易k次，所以直接在加一层k循环就可以
            //122最后的递推方程：
            //sell = Math.max(sell, buy + prices[i]);
                //buy = Math.max(buy, -prices[i]);
            profit[j] = {
                sell: Math.max(profit[j].sell, profit[j].buy + prices[i]),
                buy: Math.max(profit[j].buy, profit[j - 1].sell - prices[i]),
            };
        }
    }
    return profit[k].sell; //返回第k次清空手中的股票之后的最大利润
};

714. 买卖股票的最佳时机含手续费​

714. 买卖股票的最佳时机含手续费

给定一个整数数组 prices，其中 prices[i]表示第 i 天的股票价格 ；整数 fee 代表了交易股票的手续费用。

你可以无限次地完成交易，但是你每笔交易都需要付手续费。如果你已经购买了一个股票，在卖出它之前你就不能再继续购买股票了。

返回获得利润的最大值。

var maxProfit = function(prices, fee) {
  let length = prices.length
  let dp0 = new Array(length) // 表示不持股
  let dp1 = new Array(length) // 表示持股
  dp0[0] = 0
  dp1[0] = -prices[0] - fee
  for (let i = 1; i < length; i++) {
    dp0[i] = Math.max(dp0[i - 1], dp1[i - 1] + prices[i])
    dp1[i] = Math.max(dp1[i - 1], dp0[i - 1] - prices[i] - fee)
  }
  return dp0[length - 1]
};

309. 最佳买卖股票时机含冷冻期​

309. 最佳买卖股票时机含冷冻期

给定一个整数数组prices，其中第 prices[i] 表示第 i 天的股票价格 。

设计一个算法计算出最大利润。在满足以下约束条件下，你可以尽可能地完成更多的交易（多次买卖一支股票）:

卖出股票后，你无法在第二天买入股票 (即冷冻期为 1 天)。

状态 dp[i][0] 表示第 i 天 没有持有 股票得最大利润 dp[i][1] 表示第 i 天 持有 股票时得最大利润

状态转移方程 dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]); dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i]); 这里 i-2 是因为有冷冻期，前一天不能买，只能在 i-2 那天卖出，然后才可以买

初始状态 dp[0][0] = 0; dp[0][1] = -price[0];

var maxProfit = function(prices) {
    let len = prices.length;
    let dp = [];
    let i;
    if(prices.length <= 1){
        return 0;
    }
    for(i = 0; i<len; i++){
        dp[i] = [];
    }
    dp[0][0] = 0;
    dp[0][1] = -prices[0];
    dp[1][0] = Math.max(prices[1]-prices[0], 0);
    dp[1][1] = Math.max(dp[0][1], dp[0][0]-prices[1]);
    for(let i = 2;i<len;i++){
        dp[i][0] = Math.max(dp[i-1][0], dp[i-1][1] + prices[i]);
        dp[i][1] = Math.max(dp[i-1][1], dp[i-2][0] - prices[i]);
    }
    return dp[len-1][0];
};

状态压缩

每天可以分为三种状态:

手里有股票:r1 当手里没股票，第二天是冷冻期(也就是说今天把股票卖了):r2 手里没股票，第二天不是冷冻期(也就是说要不今天是冷冻期；要不前两天是冷冻期，冷冻期过去后一直没买股票):r3 每种状态都和前一天的状态有关：

newR1:前一天手里有股票，今天没操作 或 昨天没股票，今天买了新股票 Math.max(r1, r3 - prices[i]); newR2:前一天手里有股票，今天卖了股票 r1 + prices[i]; newR3:前一天也没买新股票 或 昨天把股票卖了，今天冷冻期，手里也没股票，明天就不是冷冻期了 Math.max(r3, r2); 肯定在最后一天或最后一天之前就把股票给卖了，否则砸手里了，Math.max(r3, r2)

var maxProfit = function(prices) {
    let n = prices.length;
    let r1 = -prices[0];
    let r2 = 0;
    let r3 = 0;
    for(let i = 1; i < n; i++) {
        let newR1 = Math.max(r1, r3 - prices[i]);
        let newR2 = r1 + prices[i];
        let newR3 = Math.max(r3, r2);
        r1 = newR1;
        r2 = newR2;
        r3 = newR3;
    }
    return Math.max(r3, r2);
};

322. 零钱兑换​

322. 零钱兑换

var coinChange = function(coins, amount) {
    let dp=new Array(amount+1).fill(Infinity)
    dp[0]=0
    for(let i=1;i<=amount;i++){
        for(let coin of  coins){
            if(i-coin>=0){
                dp[i]=Math.min(dp[i],dp[i-coin]+1)
            }
        }
    }
    return dp[amount]===Infinity?-1:dp[amount]
};

198. 打家劫舍​

198. 打家劫舍

你是一个专业的小偷，计划偷窃沿街的房屋。每间房内都藏有一定的现金，影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警。

给定一个代表每个房屋存放金额的非负整数数组，计算你 不触动警报装置的情况下 ，一夜之内能够偷窃到的最高金额。

在当前位置 n 房屋可盗窃的最大值，要么就是 n-1 房屋可盗窃的最大值，要么就是 n-2 房屋可盗窃的最大值加上当前房屋的值，二者之间取最大值

var rob = function(nums) {
    const len = nums.length;
    if(len == 0)
        return 0;
    const dp = new Array(len + 1);
    dp[0] = 0;
    dp[1] = nums[0];
    for(let i = 2; i <= len; i++) {
        dp[i] = Math.max(dp[i-1], dp[i-2] + nums[i-1]);
    }
    return dp[len];
};

213. 打家劫舍 II​

213. 打家劫舍 II

你是一个专业的小偷，计划偷窃沿街的房屋，每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ，这意味着第一个房屋和最后一个房屋是紧挨着的。同时，相邻的房屋装有相互连通的防盗系统，如果两间相邻的房屋在同一晚上被小偷闯入，系统会自动报警 。

给定一个代表每个房屋存放金额的非负整数数组，计算你 在不触动警报装置的情况下 ，今晚能够偷窃到的最高金额。

这个题目和打家劫舍类似，不过就是多了两种情况：

  • 不偷第一家
  • 不偷最后一家

这样就可以分类讨论，当不偷第一家时，就排除到第一家，对其他家进行计算，当不偷最后一家时，就排除掉最后一家，对其他家进行计算。

当前节点的最大值就是当前节点和之前的第二个节点的和与上个节点的值的最大值，这样说可能比较绕，状态转移方程代码：

dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i])
var rob = function(nums) {
    const len = nums.length
    let res1 = 0, res2 = 0
    if(len === 0) return 0
    if(len === 1) return nums[0]

    const dp = new Array(len)
    
    // 不偷第一家
    dp[0] = 0
    dp[1] = nums[1]
    for(let i = 2; i <= len - 1; i++){
        dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
    }
    res1 = dp[len - 1]

    // 不偷最后一家
    dp[0] = nums[0]
    dp[1] = Math.max(nums[0], nums[1])
    for(let i = 2; i <= len - 2; i++){
        dp[i] = Math.max(dp[i - 1], dp[i - 2] + nums[i]);
    }
    res2 = dp[len - 2]
    return Math.max(res1, res2)
};

337. 打家劫舍 III​

337. 打家劫舍 III

小偷又发现了一个新的可行窃的地区。这个地区只有一个入口，我们称之为 root 。

除了 root 之外，每栋房子有且只有一个“父“房子与之相连。一番侦察之后，聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ，房屋将自动报警。

给定二叉树的 root 。返回 在不触动警报的情况下 ，小偷能够盗取的最高金额 。

对于二叉树，每个节点都有两种状态，选中或者不选中，我们可以使用深度优先遍历来遍历这棵二叉树：

  • 当节点被选中时，它的左右孩子都不能被选中，所以最大值就是：node.val + left[1] + right[1]；
  • 当节点不被选中时，它的左右子孩子可以选中也可以不选中，所以最大值就是：Math.max(left[0], left[1]) + Math.max(right[0], right[1]);

最后返回左右子树中最大值即可。

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var rob = function(root) {
    const dfs = (node) => {
        if (node === null) {
            return [0, 0];
        }
        const left = dfs(node.left);
        const right = dfs(node.right);
      
        const select = node.val + left[1] + right[1];
        const notSelect = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
        return [select, notSelect];
    }
    const res = dfs(root)
    return Math.max(res[0], res[1])
};

392. 判断子序列​

392. 判断子序列

const isSubsequence = (s, t) => {
    // s、t的长度
    const [m, n] = [s.length, t.length];
    // dp全初始化为0
    const dp = new Array(m + 1).fill(0).map(x => new Array(n + 1).fill(0));
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            // 更新dp[i][j]，两种情况
            if (s[i - 1] === t[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + 1;
            } else {
                dp[i][j] = dp[i][j - 1];
            }
        }
    }
    // 遍历结束，判断dp右下角的数是否等于s的长度
    return dp[m][n] === m ? true : false;
};

115. 不同的子序列​

115. 不同的子序列

给定一个字符串 s 和一个字符串 t ，计算在 s 的子序列中 t 出现的个数。

字符串的一个 子序列 是指，通过删除一些（也可以不删除）字符且不干扰剩余字符相对位置所组成的新字符串。（例如，"ACE" 是 "ABCDE" 的一个子序列，而 "AEC" 不是）

image-20221007213516342

const numDistinct = (s, t) => {
    let m=s.length,n=t.length;
    const dp = Array(m + 1).fill().map(() => Array(n + 1).fill(0))
    for (let i = 0; i <= m; i++) {
        dp[i][0] = 1;
    }

    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            if (s[i - 1] === t[j - 1]) {
                dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
            } else {
                dp[i][j] = dp[i - 1][j]
            }
        }
    }

    return dp[m][n];
};

583. 两个字符串的删除操作​

583. 两个字符串的删除操作

给定两个单词 word1 和 word2 ，返回使得 word1 和 word2 相同所需的最小步数。

每步 可以删除任意一个字符串中的一个字符。

const minDistance = (word1, word2) => {
    var m=word1.length;
    var n=word2.length;
    const dp=Array(m+1).fill().map(()=>Array(n+1).fill(0))
    for(let i=1;i<=m;i++){
        dp[i][0]=i
    }
    for(let j=1;j<=n;j++){
        dp[0][j]=j
    }
    for(let i=1;i<=m;i++){
        for(let j=1;j<=n;j++){
            if(word1[i-1]===word2[j-1]) dp[i][j]=dp[i-1][j-1]
            else dp[i][j]=Math.min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2)
        }
    }
    return dp[m][n]
};

72. 编辑距离​

72. 编辑距离

给你两个单词 word1 和 word2， 请返回将 word1 转换成 word2 所使用的最少操作数 。

你可以对一个单词进行如下三种操作：

插入一个字符 删除一个字符 替换一个字符

示例 1： 输入：word1 = "horse", word2 = "ros" 输出：3 解释： horse -> rorse (将 'h' 替换为 'r') rorse -> rose (删除 'r') rose -> ros (删除 'e')

示例 2： 输入：word1 = "intention", word2 = "execution" 输出：5 解释： intention -> inention (删除 't') inention -> enention (将 'i' 替换为 'e') enention -> exention (将 'n' 替换为 'x') exention -> exection (将 'n' 替换为 'c') exection -> execution (插入 'u')

确定递推公式

在确定递推公式的时候，首先要考虑清楚编辑的几种操作，整理如下：

if (word1[i - 1] == word2[j - 1])
    不操作
if (word1[i - 1] != word2[j - 1])
    增
    删
    换

if (word1[i - 1] != word2[j - 1])，此时就需要编辑了，如何编辑呢？

  • 操作一：word1删除一个元素，那么就是以下标i - 2为结尾的word1 与 j-1为结尾的word2的最近编辑距离 再加上一个操作。

即 dp[i][j] = dp[i - 1][j] + 1;

  • 操作二：word2删除一个元素，那么就是以下标i - 1为结尾的word1 与 j-2为结尾的word2的最近编辑距离 再加上一个操作。

即 dp[i][j] = dp[i][j - 1] + 1;

word2添加一个元素，相当于word1删除一个元素，例如 word1 = "ad" ，word2 = "a"，word1删除元素'd' 和 word2添加一个元素'd'，变成word1="a", word2="ad"， 最终的操作数是一样！

操作三：替换元素，word1替换word1[i - 1]，使其与word2[j - 1]相同，此时不用增加元素，那么以下标i-2为结尾的word1 与 j-2为结尾的word2的最近编辑距离 加上一个替换元素的操作。

即 dp[i][j] = dp[i - 1][j - 1] + 1;

综上，当 if (word1[i - 1] != word2[j - 1]) 时取最小的，即：dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;

递归公式

if (word1[i - 1] == word2[j - 1]) {
    dp[i][j] = dp[i - 1][j - 1];
}
else {
    dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1;
}

dp[i][j] 表示以下标i-1为结尾的字符串word1，和以下标j-1为结尾的字符串word2，最近编辑距离为dp[i][j]。

那么dp[i][0] 和 dp[0][j] 表示什么呢？

dp[i][0] ：以下标i-1为结尾的字符串word1，和空字符串word2，最近编辑距离为dp[i][0]。

那么dp[i][0]就应该是i，对word1里的元素全部做删除操作，即：dp[i][0] = i;

同理dp[0][j] = j;

139. 单词拆分​

139. 单词拆分

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。

注意：不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

const wordBreak = (s, wordDict) => {

    let dp = Array(s.length + 1).fill(false);
    dp[0] = true;

    for(let i = 0; i <= s.length; i++){
        for(let j = 0; j < wordDict.length; j++) {
            if(i >= wordDict[j].length) {
                if(s.slice(i - wordDict[j].length, i) === wordDict[j] && dp[i - wordDict[j].length]) {
                    dp[i] = true
                }
            }
        }
    }

    return dp[s.length];
}

设计数据结构​

146. LRU 缓存​

146. LRU 缓存

/**
 * @param {number} capacity
 */
var LRUCache = function(capacity) {
    this.map = new Map();
    this.capacity = capacity;
};

/** 
 * @param {number} key
 * @return {number}
 */
LRUCache.prototype.get = function(key) {
    if(this.map.has(key)){
        let value = this.map.get(key);
        this.map.delete(key); // 删除后，再 set ，相当于更新到 map 最后一位
        this.map.set(key, value);
        return value
    } else {
        return -1
    }
};

/** 
 * @param {number} key 
 * @param {number} value
 * @return {void}
 */
LRUCache.prototype.put = function(key, value) {
    // 如果已有，那就要更新，即要先删了再进行后面的 set
    if(this.map.has(key)){
        this.map.delete(key);
    }
    this.map.set(key, value);
    // put 后判断是否超载
    if(this.map.size > this.capacity){
        this.map.delete(this.map.keys().next().value);
    }

};

/**
 * Your LRUCache object will be instantiated and called as such:
 * var obj = new LRUCache(capacity)
 * var param_1 = obj.get(key)
 * obj.put(key,value)
 */

155. 最小栈​

155. 最小栈