跳到主要内容

WebGL入门与实践

认识WebGL​

WebGL 是一组基于 JavaScript 语言的图形规范，浏览器厂商按照这组规范进行实现，为 Web 开发者提供一套3D图形相关的 API。那么，这些 API 能够帮助 Web 开发者做些什么呢？

这些 API 能够让 Web 开发者使用 JavaScript 语言直接和显卡（GPU）进行通信。当然 WebGL 的 GPU 部分也有对应的编程语言，简称 GLSL。我们用它来编写运行在 GPU 上的着色器程序。着色器程序需要接收 CPU（WebGL 使用 JavaScript） 传递过来的数据，然后对这些数据进行流水线处理，最终显示在屏幕上，进而实现丰富多彩的 3D 应用，比如 3D 图表，网页游戏，3D 地图，WebVR 等

WebGL 只能够绘制点、线段、三角形这三种基本图元，但是我们经常看到 WebGL 程序中含有立方体、球体、圆柱体等规则形体，甚至很多更复杂更逼真的不规则模型，那么 WebGL 是如何绘制它们的呢？其实这些模型本质上是由一个一个的点组成，GPU 将这些点用三角形图元绘制成一个个的微小平面，这些平面之间互相连接，从而组成各种各样的立体模型

构建模型顶点数据​

一般情况下，最初的顶点坐标是相对于模型中心的，不能直接传递到着色器中，我们需要对顶点坐标按照一系列步骤执行模型转换，视图转换，投影转换，转换之后的坐标才是 WebGL 可接受的坐标，即裁剪空间坐标。我们把最终的变换矩阵和原始顶点坐标传递给 GPU，GPU 的渲染管线对它们执行流水线作业。

渲染管线过程​

  • 首先进入顶点着色器阶段，利用 GPU 的并行计算优势对顶点逐个进行坐标变换。
  • 然后进入图元装配阶段，将顶点按照图元类型组装成图形。
  • 接下来来到光栅化阶段，光栅化阶段将图形用不包含颜色信息的像素填充。
  • 在之后进入片元着色器阶段，该阶段为像素着色，并最终显示在屏幕上。

着色器​

GLSL 是用来编写着色器程序的语言，那么新的问题来了，着色器程序是用来做什么的呢？ 简单地说，着色器程序是在显卡（GPU）上运行的简短程序，代替了 GPU 固定渲染管线的一部分，使 GPU 渲染过程中的某些部分允许开发者通过编程进行控制

着色器程序允许我们通过编程来控制 GPU 的渲染

img

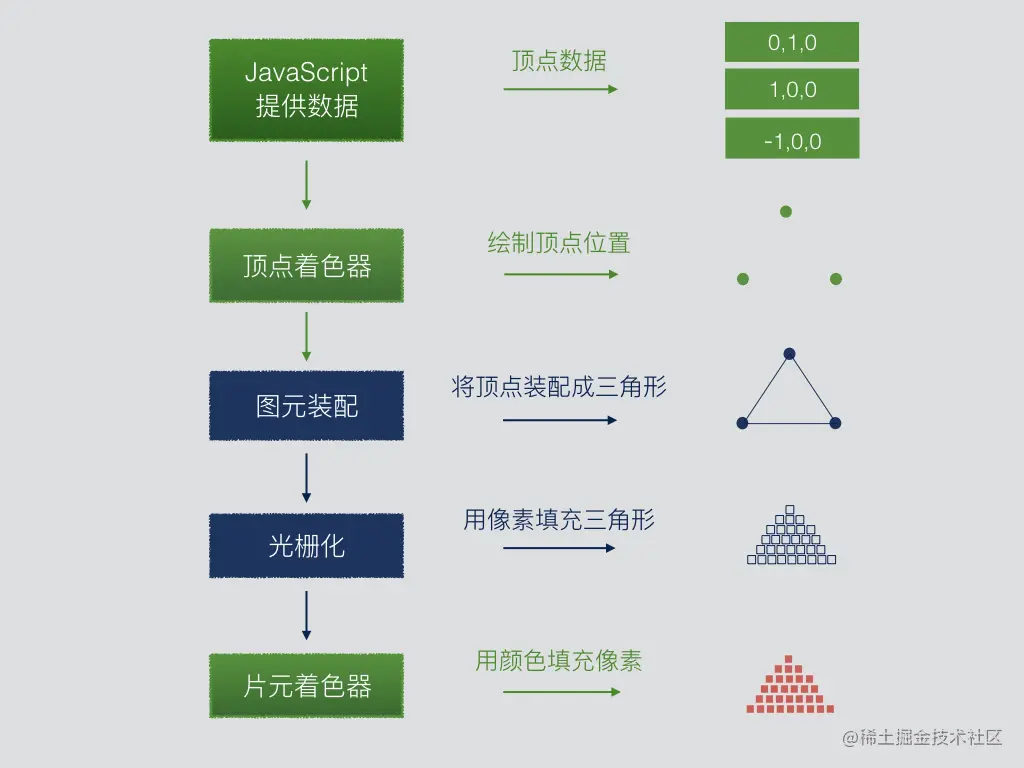
上图简单演示了 WebGL 对一个红色三角形的渲染过程，绿色部分为开发者可以通过编程控制的部分：

  • JavaScript 程序 处理着色器需要的顶点坐标、法向量、颜色、纹理等信息，并负责为着色器提供这些数据，上图为了演示方便，只是提供了三角形顶点的位置数据。
  • 顶点着色器 接收 JavaScript 传递过来的顶点信息，将顶点绘制到对应坐标。
  • 图元装配阶段 将三个顶点装配成指定图元类型，上图采用的是三角形图元。
  • 光栅化阶段 将三角形内部区域用空像素进行填充。
  • 片元着色器 为三角形内部的像素填充颜色信息，上图为暗红色。

实际上，对顶点信息的变换操作既可以在 JavaScript 中进行，也可以在着色器程序中进行。通常我们都是在 JavaScript 中生成一个包含了所有变换的最终变换矩阵，然后将该矩阵传递给着色器，利用 GPU 并行计算优势对所有顶点执行变换

GLSL基本语法​

GLSL 属于 GPU 层面的编程语言，因此它必须有能力支持图形相关的操作。除了绘制 API，还要支持各种数学运算，主要体现在向量和矩阵。

GLSL 主要是在 C 语言的基础上新增了一些内置变量、数据类型和数学函数，因为是基于 C 语言的拓展，所以在语法规则上和 C 语言基本相同。

变量命名​

GLSL 的语法和 C 语言类似，因此 GLSL 的变量命名方式和 C 语言基本一致。但由于 GLSL 新增了一些数据类型、内置属性和保留前缀，所以变量命名除了满足 C 语言的命名规则之外，还要满足 GLSL 的特殊规则：

  • 不能以 gl_ 作为前缀，gl_ 开头的变量被用于定义 GLSL 的内部变量，这是 GLSL 保留的命名前缀。
  • GLSL 的一些保留名称也不能作为变量名称，比如 attribute、uniform、varying 等。

数据类型​

GLSL 最突出的部分是新增了向量和矩阵相关的数据类型，比如存储向量的容器 vec{n}，存储四阶矩阵的容器mat4，2D纹理采样器 sampler2D，3D纹理采样器samplerCube等等。下面我们着重介绍向量和矩阵在 GLSL 中的用法。

向量​

向量是 GLSL 中很重要的一种数据类型，着色器程序的很多地方都需要用到向量，用来储存包含多个分量的数据，比如颜色信息、齐次坐标、法向量等。

向量按照维度分为2维、3维、4维，按照存储的数据类型分为浮点向量vec{n}，整型向量ivec{n}，布尔向量bvec{n}。

浮点向量​

  • vec2：存储2个浮点数。
  • vec3：存储3个浮点数。
  • vec4：存储4个浮点数。

浮点向量的赋值相对浮点数宽松一些，比如在为一个浮点变量赋值的时候，我们必须这样写：

  • 正确
float size = 10.0;

像下面这样赋值就会报错，因为类型不匹配，size 是浮点变量，10 是一个整数，变量类型和要赋值的类型不匹配。

  • 错误
float size = 10;

但是在为向量赋值时，就会宽松一些，比如我们构建一个2维浮点向量，分量都是 1。

我们可以这样写：

  • 正确
vec2 texcoords = vec2(1.0, 1.0);

也可以这样写：

vec2 texcoords = vec2(1, 1);

vec 向量类型会自动对元素做类型转换。

之所以讲这些细节，有一个原因是 GLSL 程序的调试有一定局限性，没有特别好用的调试器能够让我们逐行逐变量地进行调试，所以我们只能减少低级失误。

怎样才能减少低级失误？只有夯实基础。但减少失误并不意味着消除，即使我们万般小心，也仍然会出现问题导致编译或者运行异常，这时只能用肉眼排查问题。拥有好的基础，也会促使你很快地找到问题产生的原因。

整型向量​

  • ivec2：存储2个整数。
  • ivec3：存储3个整数。
  • ivec4：存储4个整数。

整型向量和浮点向量类似，向量的各个元素都是整型数字，此处不做重复讲解。

布尔向量​

  • bvec2：存储2个布尔值。
  • bvec3：存储3个布尔值。
  • bvec4：存储4个布尔值。

布尔向量的各个元素都是布尔值true或者false，此处也不做重复讲解。

向量的使用技巧​

每个向量我们都可以用 {s、t、p、q},{r、g、b、a},{x、y、z、w}来表示。获取各个位置的元素，我们可以使用.操作符。

比如一个 4 维向量：

vec4 v = vec(1, 2, 3, 4);

那么v.s、v.r、v.x、v[0]表示的是该向量第 1 个位置的元素。

同理：

  • v.t、v.g、v.y、v[1]表示的是该向量第 2 个位置的元素。
  • v.p、v.b、v.z、v[2]表示的是该向量第 3个位置的元素。
  • v.q、v.a、v.w、v[3]表示的是该向量第 4 个位置的元素。

除此之外，我们还可以使用这种方式对低维向量赋值，假设我们有一个 4 维向量 v，现在想以 v 的前两个元素创建一个 2 维向量 v1，那么我们可以这样赋值：

vec4 v = vec4(1, 2, 3, 4);

// xyzw 方式赋值
vec2 v1 = v.xy;
// stpq 赋值
vec2 v1 = v.st;
// rgba 赋值
vec2 v1 = v.rg;

// 构造函数式
vec2 v1 = vec2(v.x, v.y);
vec2 v1 = vec2(v.s, v.t);
vec2 v1 = vec2(v.r, v.g);

还可以这样使用：

vec4 v = vec4(1, 2, 3, 4)
vec2 v1 = vec2(v.xx);

通过 v.xx 的方式将 v1 的两个元素设置成 v 的第一个元素值，变成 (1, 1)。

向量的运算规则​

GLSL 中关于向量的另一个重要部分就是运算规则，向量的运算对象分为如下几类：

向量和基础数字类型的运算。

向量和基础数字类型之间的运算比较简单，规则是将数字和向量的各个分量进行运算，并返回新的向量。

假设有一个 4 维向量 v(x, y, z, w)，浮点数 f。

向量 v 和 f 之间的加减乘除运算，GLSL 会将各个分量分别和数字 f 进行加减乘除，并返回新的向量 v1。

// 加法
vec4 v1 = v + f = (x + f, y + f, z + f, w + f);
// 减法
vec4 v1 = v - f = (x - f, y - f, z - f, w - f);
// 乘法
vec4 v1 = v * f = (x * f, y * f, z * f, w * f);
// 除法
vec4 v1 = v / f = (x / f, y / f, z / f, w / f);

向量和向量之间的运算

向量和向量之间也可以进行运算，返回一个新的向量，前提是两个向量之间的维度必须相同。

运算规则是两个向量对应位置的元素分别进行运算。

假设向量 v1 (x1, y1, z1, w1)，向量 v2（x2, y2, z2, w2），那么有：

// 加法
vec4 v3 = v1 + v2 = (x1 + x2, y1 + y2, z1 + z2, w1 + w2);
// 减法
vec4 v3 = v1 - v2 = (x1 - x2, y1 - y2, z1 - z2, w1 - w2);

// 乘法
vec4 v3 = v1 * v2 = (v1 * v2, y1 * y2, z1 * z2, w1 * w2);
// 减法
vec4 v3 = v1 / v2 = (x1 / x2, y1 / y2, z1 / z2, w1 / w2);

看起来很简单，但是有一点需要注意，向量之间乘法有三种，上面的 * 号乘法规则是为了使用方便。

在数学领域，向量之间还有两种乘法点乘和叉乘，具体区别我们在中级进阶 --- 数学：点、向量、矩阵章节详细介绍。

GLSL 中增加了两种内置函数，用来实现点乘和叉乘运算，它们分别是 dot和cross，使用起来也很简单：

// 点乘
float v3 = dot(v1, v2);

// 叉乘
vec3 v3 = cross(v1, v2);

在计算光照效果时，会经常使用这两个函数。

以上就是向量相关内容，大多数运算规则和线性代数一致。

矩阵​

矩阵是 GLSL 中和数学相关的另一块重要内容，在着色器程序中，我们会经常使用矩阵来完成各种变换，比如坐标转换、计算光照时的法向量转换等。

矩阵分类​

矩阵按照维度分为二阶、三阶、四阶，其中三阶和四阶矩阵用的较多，我们下面主要讲解四阶矩阵。

四阶矩阵​

四阶矩阵，包含 4 行 4 列共 16 个浮点数，在着色器程序中初始化一个四阶矩阵有很多种方式。

  • 用 16 个浮点数构造矩阵。

这是最简单最直观的构造方式：

mat4 m = mat4(
    1, 2, 3, 4,  //第一列
    5, 6, 7, 8,  //第二列
    9, 10, 11, 12, //第三列
    13, 14, 15,16 // 第四列
);
  • 用 1 个浮点数构造对角线矩阵。
mat4 a = mat4(1.0);

mat4 传入一个浮点数构造出的矩阵，对角线上的值都是 1.0:

[      1.0, 0, 0, 0,    0, 1.0, 0, 0,    0, 0, 1.0, 0,    0, 0, 0, 1.0]
  • 利用列向量构造

四阶矩阵可以理解为四个列向量组合而成，所以 GLSL 提供了利用向量构造矩阵的方法。

//第一列
vec4 c0 = vec4(1, 2, 3, 4);
//第二列
vec4 c1 = vec4(5, 6, 7, 8);
//第三列
vec4 c2 = vec4(1, 2, 3, 4);
//第四列
vec4 c3 = vec4(5, 6, 7, 8);

mat4 m = mat4(c0, c1, c2, c4);
  • 向量与浮点数混合构造。 当然除了纯数字构造、纯向量构造，GLSL 也允许向量和数字混合构造：
vec4 c0 = vec4(1, 2, 3, 4);
vec4 c1 = vec4(5, 6, 7, 8);
vec4 c2 = vec4(1, 2, 3, 4);

mat4 m = mat4(c0, c1, c2, 5, 6, 7, 8);

观察上面的构造方式，我们发现，mat4构造函数 中传入的数字只要满足 16 个就可以构造成四阶矩阵。

所以，大家还可以想到利用二维、三维向量进行构造的方式。

总之，GLSL 为矩阵提供的构造方式很灵活，毕竟，在 GLSL 中我们用的最多的除了向量就是矩阵了。

  • 矩阵运算
乘法运算​

我们用的最多的就是乘法运算了，在GLSL 中，矩阵乘法用 * 来表示，但大家要记住，由于 GLSL 中矩阵采用的是列主序，所以，矩阵和向量相乘时，要置在乘号左侧，如下：

mat4 m = mat4(1.0);
vec4 v1 = m * vec4(1, 2, 3, 4);

还有一些其他的矩阵运算方法，比如转置、求逆等：

mat4 m0 = mat4(1.0);
// 转置
mat4 m1 = transpose(m0);
// 求逆
mat4 m2 = inverse(m0)

内置变量​

内置属性在前面章节中已经学过一些了，比如大家很熟悉的 gl_Position、gl_FragColor 等，除此之外，还有一些不常用的属性。

顶点着色器​

  • gl_Position：顶点坐标。
  • gl_PointSize：点的尺寸。
  • gl_Normal：顶点法线。

片元着色器​

  • gl_FragColor，当前片元的颜色，类型 vec4。
  • gl_FragCoord，屏幕像素的x，y，z，1 / w。
  • gl_FragDepth，片元的最终深度值，在后面的深度测试用到，在片元着色器中我们无法修改x, y值，但是可以修改z值。

内置函数​

GLSL 内置了很多数学函数，下面列举一些经常用到的。

向量函数​

函数作用
cross计算两个向量的叉积
dot计算向量的点积。
normalize归一化向量，返回一个和原向量方向相同，但是长度为1的单位向量。
reflect根据入射向量和法线向量，计算出反射向量。
length计算向量的长度
distance计算两个向量之间的距离。

常用数学函数​

函数作用
abs将某个数的绝对值
floor返回不大于某个数的最大整数。
round四舍五入值
ceil返回大于某个数的最小整数。
fract返回浮点数的小数部分
mod取模
min返回两个数中比较小的数
max返回两个数中比较大的数

三角函数​

GLSL 提供了很多三角函数，方便我们进行角度求值：

函数作用
radians将角度（如90度）转化为弧度（PI/2）。
degrees将弧度（如PI / 2）转化为角度（90 度）。
sin求弧度的正弦
cos求弧度的余弦
tan求弧度的正切
asin根据正弦值求对应的弧度
acos根据余弦值求对应的弧度
atan根据正切值求对应的弧度

以上就是常用的三角函数，GLSL 还提供了一些更复杂但是不常用的函数，此处不一一列举了，大家感兴趣的话可以查查 GLSL 语法规范。

限定符​

限定符在之前章节也已经陆续讲过了，再次做个总结。

attribute​

attribute 变量只能定义在顶点着色器中，它的作用是接收 JavaScript 程序传递过来的与顶点有关的数据，比如在之前程序中定义的顶点颜色、法线、坐标等，它们是顶点的属性。

也就是说，如果有一类数据，它是跟随顶点而存在的，每个顶点所对应的数据不尽相同，那么我们就需要用 attribute 限定符定义变量。

uniform​

uniform 用来修饰全局变量，它既可以在顶点着色器中定义，也可以在片元着色器中定义，用来接收与顶点无关的数据。

比如，在之前程序中，我们定义了一个 uniform 变量 u_Matrix，它用来接收 JavaScript 中传递过来的 模型视图投影矩阵，该数据与顶点无关，也就是每个顶点共用变换矩阵，所以我们应该用 uniform 修饰该变量。

varying​

varying变量一般是成对定义的，即在顶点着色器中定义，在片元着色器中使用。它所修饰的变量在传递给片元着色器之前会进行插值化处理。

绘制点(点击随机出颜色)​

基本概念​

  • 图元：WebGL 能够绘制的基本图形元素，包含三种：点、线段、三角形。
  • 片元：可以理解为像素，像素着色阶段是在片元着色器中。
  • 裁剪坐标系：裁剪坐标系是顶点着色器中的 gl_Position 内置变量接收到的坐标所在的坐标系。
  • 设备坐标系：又名 NDC 坐标系，是裁剪坐标系各个分量对 w 分量相除得到的坐标系，特点是 x、y、z 坐标分量的取值范围都在 【-1，1】之间，可以将它理解为边长为 2 的正方体，坐标系原点在正方体中心。

着色器代码​

  • 顶点着色器

顶点着色器的主要任务是告诉 GPU 在裁剪坐标系的原点（也就是屏幕中心）画一个大小为 10 的点。

void main(){
    //声明顶点位置
    gl_Position = vec4(0.0, 0.0, 0.0, 1.0);
    //声明待绘制的点的大小。
    gl_PointSize = 10.0;
}
  • 片元着色器

顶点着色器中的数据经过图元装配和光栅化之后，来到了片元着色器，在本例中，片元着色器的任务是通知 GPU 将光栅化后的像素渲染成红色，所以片元着色器要对内置变量 gl_FragColor （代表像素要填充的颜色）进行赋值。

void main(){
    //设置像素的填充颜色为红色。
    gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0); 
}
  • gl_Position、gl_PointSize、gl_FragColor 是 GLSL 的内置属性。
    • gl_Position：顶点的裁剪坐标系坐标，包含 X, Y, Z，W 四个坐标分量，顶点着色器接收到这个坐标之后，对它进行透视除法，即将各个分量同时除以 W，转换成 NDC 坐标，NDC 坐标每个分量的取值范围都在【-1, 1】之间，GPU 获取这个属性值作为顶点的最终位置进行绘制。
    • gl_FragColor：片元（像素）颜色，包含 R, G, B, A 四个颜色分量，且每个分量的取值范围在【0,1】之间，GPU 获取这个值作为像素的最终颜色进行着色。
    • gl_PointSize：绘制到屏幕的点的大小，需要注意的是，gl_PointSize只有在绘制图元是点的时候才会生效。当我们绘制线段或者三角形的时候，gl_PointSize是不起作用的。
  • vec4：包含四个浮点元素的容器类型，vec 是 vector（向量）的单词简写，vec4 代表包含 4 个浮点数的向量。此外，还有 vec2、vec3 等类型，代表包含2个或者3个浮点数的容器。
  • GLSL 中 gl_Position 所接收的坐标所在坐标系是裁剪坐标系 ，不同于我们的浏览器窗口坐标系。所以当我们赋予 gl_Position 位置信息的时候，需要对其进行转换才能正确显示。
  • gl_FragColor，属于 GLSL 内置属性，用来设置片元颜色，包含 4 个分量 (R, G, B, A)，各个颜色分量的取值范围是【0，1】，也不同于我们常规颜色的【0，255】取值范围，所以当我们给 gl_FragColor 赋值时，也需要对其进行转换。平常我们所采用的颜色值（R, G, B, A），对应的转换公式为： (R值/255，G值/255，B值/255，A值/1）。拿红色举例，在CSS中，红色用 RGBA 形式表示是（255，0，0，1），那么转换成 GLSL 形式就是(255 / 255, 0 / 255, 0 / 255, 1 / 1)，转换后的值为（1.0, 0.0, 0.0, 1.0)。

GLSL 是强类型语言，定义变量时，数据类型和值一定要匹配正确，比如我们给浮点数 a 赋值 1，我们需要这样写：float a = 1.0; 如果用 float a = 1; 的话会报错。

着色器源码本质是字符串，所以我们既可以把着色器源码存储在 JavaScript 变量里，也可以放在 script 标签里，甚至存储在数据库中并通过 ajax 请求获取。

HTML代码​

HTML 文件至少需要包含一个 canvas 标签，另外需要两个存储着色器源码的 script 标签

<body>
    <!-- 顶点着色器源码 -->
    <script type="shader-source" id="vertexShader">
     void main(){
        //声明顶点位置
        gl_Position = vec4(0.0, 0.0, 0.0, 1.0);
        //声明要绘制的点的大小。
        gl_PointSize = 10.0;
    }
    </script>
    
    <!-- 片元着色器源码 -->
    <script type="shader-source" id="fragmentShader">
     void main(){
        //设置像素颜色为红色
        gl_FragColor = vec4(1.0, 0.0, 0.0, 1.0); 
    }
    </script>
    
    <canvas id="canvas"></canvas>
</body>

JavaScipt代码​

获取 WebGL 绘图环境​

var canvas = document.querySelector('#canvas');
var gl = canvas.getContext('webgl') || canvas.getContext("experimental-webgl");

创建顶点着色器对象​

// 获取顶点着色器源码
var vertexShaderSource = document.querySelector('#vertexShader').innerHTML;
// 创建顶点着色器对象
var vertexShader = gl.createShader(gl.VERTEX_SHADER);
// 将源码分配给顶点着色器对象
gl.shaderSource(vertexShader, vertexShaderSource);
// 编译顶点着色器程序
gl.compileShader(vertexShader);

创建片元着色器对象​

// 获取片元着色器源码
var fragmentShaderSource = document.querySelector('#fragmentShader').innerHTML;
// 创建片元着色器程序
var fragmentShader = gl.createShader(gl.FRAGMENT_SHADER);
// 将源码分配给片元着色器对象
gl.shaderSource(fragmentShader, fragmentShaderSource);
// 编译片元着色器
gl.compileShader(fragmentShader);

创建着色器程序​

//创建着色器程序
var program = gl.createProgram();
//将顶点着色器挂载在着色器程序上。
gl.attachShader(program, vertexShader); 
//将片元着色器挂载在着色器程序上。
gl.attachShader(program, fragmentShader);
//链接着色器程序
gl.linkProgram(program);

启用着色器程序​

// 使用刚创建好的着色器程序。
gl.useProgram(program);

开始绘制​

//设置清空画布颜色为黑色。
gl.clearColor(0.0, 0.0, 0.0, 1.0);

//用上一步设置的清空画布颜色清空画布。
gl.clear(gl.COLOR_BUFFER_BIT);

//绘制点。
gl.drawArrays(gl.POINTS, 0, 1);

void gl.drawArrays(mode, first, count);

  • 参数：
    • mode，代表图元类型。
    • first，代表从第几个点开始绘制。
    • count，代表绘制的点的数量。

gl.drawArrays 是执行绘制的 API，上面示例中的第一个参数 gl.POINTS 代表我们要绘制的是点图元，第二个参数代表要绘制的顶点的起始位置，第三个参数代表顶点绘制个数。

代码封装​

//获取canvas
var canvas = getCanvas(id);

//获取webgl绘图环境
var gl = getWebGLContext(canvas);

//创建顶点着色器
var vertexShader = createShaderFromScript(gl, gl.VERTEX_SHADER,'vertexShader');
//创建片元着色器
var fragmentShader = createShaderFromScript(gl, gl.FRAGMENT_SHADER,'fragmentShader');

//创建着色器程序
var program = createProgram(gl ,vertexShader, fragmentShader);
//告诉 WebGL 运行哪个着色器程序
gl.useProgram(program);

//设置清空画布颜色为黑色。
gl.clearColor(0.0, 0.0, 0.0, 1.0);
//用上一步设置的清空画布颜色清空画布。
gl.clear(gl.COLOR_BUFFER_BIT);
//绘制点
gl.drawArrays(gl.POINTS, 0, 1);

动态点绘制​

通过 JavaScript 往着色器程序中传入顶点位置和颜色数据，从而改变点的位置和颜色

着色器代码​

  • 顶点着色器
//设置浮点数精度为中等精度
precision mediump float;
//接收点在 canvas 坐标系上的坐标 (x, y)
attribute vec2 a_Position;
//接收 canvas 的宽高尺寸
attribute vec2 a_Screen_Size;
void main(){
    //start 将屏幕坐标系转化为裁剪坐标（裁剪坐标系）
   vec2 position = (a_Position / a_Screen_Size) * 2.0 - 1.0; 
   position = position * vec2(1.0, -1.0);
   gl_Position = vec4(position, 0, 1);
   //end 将屏幕坐标系转化为裁剪坐标（裁剪坐标系）
   //声明要绘制的点的大小。
   gl_PointSize = 10.0;
}

在顶点着色器中定义两个 attribute 变量： a_Position 和 a_Screen_Size，a_Position 接收 canvas 坐标系下的点击坐标。 vec2 代表存储两个浮点数变量的容器

a_Screen_Size 变量用来接收 JavaScript 传递过来的 canvas 的宽高尺寸

vec2 position = (a_Position / a_Screen_Size) * 2.0 - 1.0

将浏览器窗口坐标转换成裁剪坐标，之后通过透视除法，除以 w 值（此处为 1 ）转变成设备坐标（NDC坐标系）。这个算法首先将(x,y) 转化到[0, 1]区间，再将 [0,1]之间的值乘以2转化到[0,2]区间，之后再减去1，转化到[-1,1]之间的值，即 NDC 坐标

  • 片元着色器
//设置浮点数精度为中等精度
precision mediump float;
//接收 JavaScript 传过来的颜色值（RGBA）。
uniform vec4 u_Color;
void main(){
    //将普通的颜色表示转化为 WebGL 需要的表示方式，即将【0-255】转化到【0,1】之间。
   vec4 color = u_Color / vec4(255, 255, 255, 1);
   gl_FragColor = color; 
}

片元着色器定义了一个全局变量 (被 uniform 修饰的变量) ，用来接收 JavaScript 传递过来的随机颜色

  • attribue 变量：只能在顶点着色器中定义。
  • uniform 变量：既可以在顶点着色器中定义，也可以在片元着色器中定义。
  • 最后一种变量类型 varing 变量：它用来从顶点着色器中往片元着色器传递数据。使用它我们可以在顶点着色器中声明一个变量并对其赋值，经过插值处理后，在片元着色器中取出插值后的值来使用。

JavaScript代码​

动态绘制点的逻辑是：

  • 声明一个数组变量 points，存储点击位置的坐标。
  • 绑定 canvas 的点击事件。
  • 触发点击操作时，把点击坐标添加到数组 points 中。
  • 遍历每个点执行 drawArrays(gl.Points, 0, 1) 绘制操作。
//找到顶点着色器中的变量a_Position
var a_Position = gl.getAttribLocation(program, 'a_Position');
//找到顶点着色器中的变量a_Screen_Size
var a_Screen_Size = gl.getAttribLocation(program, 'a_Screen_Size');
//找到片元着色器中的变量u_Color
var u_Color = gl.getUniformLocation(program, 'u_Color');
//为顶点着色器中的 a_Screen_Size 传递 canvas 的宽高信息
gl.vertexAttrib2f(a_Screen_Size, canvas.width, canvas.height);
//存储点击位置的数组。
var points = [];
canvas.addEventListener('click', e => {
   var x = e.pageX;
   var y = e.pageY;
   var color = randomColor();
   points.push({ x: x, y: y, color: color })
   gl.clearColor(0, 0, 0, 1.0);
   //用上一步设置的清空画布颜色清空画布。
    gl.clear(gl.COLOR_BUFFER_BIT);
   for (let i = 0; i < points.length; i++) {
     var color = points[i].color;
     //为片元着色器中的 u_Color 传递随机颜色
     gl.uniform4f(u_Color, color.r, color.g, color.b, color.a);
     //为顶点着色器中的 a_Position 传递顶点坐标。
     gl.vertexAttrib2f(a_Position, points[i].x, points[i].y);
     //绘制点
     gl.drawArrays(gl.POINTS, 0, 1);
   }
 })
 // 设置清屏颜色
 gl.clearColor(0, 0, 0, 1.0);
 // 用上一步设置的清空画布颜色清空画布。
 gl.clear(gl.COLOR_BUFFER_BIT);

坐标系​

WebGL中应用了很多类型的坐标系，他们分别是：

模型坐标系（object space） 世界坐标系（world space）

观察坐标系（view space）

裁剪坐标系（clip space）

规范化的设备坐标系（NDC，normalized device coordinates）

屏幕坐标系（screen space）

img

总结​

  • GLSL
    • gl_Position： 内置变量，用来设置顶点坐标。
    • gl_PointSize： 内置变量，用来设置顶点大小。
    • vec2：2 维向量容器，可以存储 2 个浮点数。
    • gl_FragColor： 内置变量，用来设置像素颜色。
    • vec4：4 维向量容器，可以存储 4 个浮点数。
    • precision：精度设置限定符，使用此限定符设置完精度后，之后所有该数据类型都将沿用该精度，除非单独设置。
    • 运算符：向量的对应位置进行运算，得到一个新的向量。
      • vec 浮点数： vec2(x, y) 2.0 = vec(x 2.0, y 2.0)。
      • vec2 vec2：vec2(x1, y1) vec2(x2, y2) = vec2(x1 x2, y1 y2)。
      • 加减乘除规则基本一致。但是要注意一点，如果参与运算的是两个 vec 向量，那么这两个 vec 的维数必须相同。
  • JavaScript 程序如何连接着色器程序
    • createShader：创建着色器对象
    • shaderSource：提供着色器源码
    • compileShader：编译着色器对象
    • createProgram：创建着色器程序
    • attachShader：绑定着色器对象
    • linkProgram：链接着色器程序
    • useProgram：启用着色器程序
  • JavaScript 如何往着色器中传递数据
    • getAttribLocation：找到着色器中的 attribute 变量地址。
    • getUniformLocation：找到着色器中的 uniform 变量地址。
    • vertexAttrib2f：给 attribute 变量传递两个浮点数。
    • uniform4f：给uniform变量传递四个浮点数。
  • WebGL 绘制函数
    • drawArrays: 用指定的图元进行绘制。
  • WebGL 图元
    • gl.POINTS: 将绘制图元类型设置成点图元。

绘制三角形(点击绘制三角形)​

三角形图元的分类​

  • 基本三角形（TRIANGLES）

基本三角形是一个个独立的三角形，假如我们提供给着色器六个顶点，那么 WebGL 会绘制两个三角形，前三个顶点绘制一个，后三个顶点绘制另一个，互不相干。 举个例子来说，假如我们有六个顶点【v1, v2, v3, v4, v5, v6】

【v1, v2, v3】为一个三角形，【v4, v5, v6】 为另一个三角形。

绘制三角形的数量 = 顶点数 / 3

img

  • 三角带（TRIANGLE_STRIP）

同样是这六个顶点，如果采用三角带的方式绘制的话，则会绘制 【v1, v2, v3】, 【v3, v2, v4】, 【v3, v4, v5】, 【v5, v4, v6】 共计 4 个三角形

img

绘制三角形的数量 = 顶点数 - 2

  • 三角扇（TRIANGLE_FAN）

三角扇的绘制方式是以第一个顶点作为所有三角形的顶点进行绘制的。采用三角扇绘制方式所能绘制的三角形的数量和顶点个数的关系如下：

绘制三角形的数量 = 顶点数 - 2

img

绘制基本三角形​

顶点着色器​

//设置浮点数据类型为中级精度
precision mediump float;
//接收顶点坐标 (x, y)
attribute vec2 a_Position;

void main(){
   gl_Position = vec4(a_Position, 0, 1);
}

片元着色器​

//设置浮点数据类型为中级精度
precision mediump float;
//接收 JavaScript 传过来的颜色值（rgba）。
uniform vec4 u_Color;

void main(){
   vec4 color = u_Color / vec4(255, 255, 255, 1);
   gl_FragColor = color;
}

JavaScript代码​

首先，定义三角形的三个顶点：

var positions = [1,0, 0,1, 0,0];

给着色器传递顶点数据和上节采用的方式不同，区别在于如何将三角形的三个顶点数据传递到顶点着色器中。 按照惯例，我们还是先找到 a_Position 变量：

var a_Position = gl.getAttribLocation(program, 'a_Position')

找到了该变量，接下来我们该怎么传递数据呢？按照上节绘制点的方式传递数据肯定不行了，因为这次我们要传递多个顶点数据。这里我们借助一个强大的工具缓冲区，通过缓冲区我们可以向着色器传递多个顶点数据。

首先创建一个缓冲区：

var buffer = gl.createBuffer();

缓冲区创建好了，我们绑定该缓冲区为 WebGL 当前缓冲区 gl.ARRAY_BUFFER，绑定之后，对缓冲区绑定点的的任何操作都会基于该缓冲区（即buffer） 进行。

gl.bindBuffer(gl.ARRAY_BUFFER, buffer);

接下来往当前缓冲区（即上一步通过 bindBuffer 绑定的缓冲区）中写入数据。

gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(positions), gl.STATIC_DRAW);

注意，着色器程序中的变量需要强类型数据，所以我们在往缓冲区写数据的时候，JS 的弱类型数组一定要用类型化数组转化一下。上面的 new Float32Array(positions)，目的就是将 JavaScript 中的弱类型数组转化为强类型数组。

步骤：

  • 首先，创建了一个保存顶点坐标的数组，保存了三角形的顶点信息。
  • 然后我们使用gl.createBuffer创建了一个缓冲区，并通过gl.bindBuffer(gl.ARRAY_BUFFER, buffer)绑定 buffer 为当前缓冲区。
  • 之后我们用new Float32Array(positions)将顶点数组转化为更严谨的类型化数组。
  • 最后我们使用 gl.bufferData 将类型化后的数组复制到缓冲区中，最后一个参数 gl.STATIC_DRAW 提示 WebGL 我们不会频繁改变缓冲区中的数据，WebGL 会根据这个参数做一些优化处理。

把顶点组成的模型渲染到屏幕

需要告诉 WebGL 如何从之前创建的缓冲区中获取数据，并且传递给顶点着色器中的 a_Position 属性。 那么，首先启用对应属性 a_Position：

gl.enableVertexAttribArray(a_Position);

接下来我们需要设置从缓冲区中取数据的方式：

//每次取两个数据
var size = 2;
//每个数据的类型是32位浮点型
var type = gl.FLOAT;  
//不需要归一化数据
var normalize = false; 
// 每次迭代运行需要移动数据数 * 每个数据所占内存 到下一个数据开始点。
var stride = 0;   
// 从缓冲起始位置开始读取     
var offset = 0; 
// 将 a_Position 变量获取数据的缓冲区指向当前绑定的 buffer。
gl.vertexAttribPointer(
   a_Position, size, type, normalize, stride, offset)

需要注意的是，我们通过 gl.vertexAttribPointer 将属性绑定到了当前的缓冲区，即使之后我们使用 bindBuffer 绑定到其他缓冲区时，a_Position 也依然会从 buffer 这个缓冲区中获取数据。

  • gl.vertexAttribPointer (target, size, type, normalize, stride, offset)。
    • target： 允许哪个属性读取当前缓冲区的数据。
    • size：一次取几个数据赋值给 target 指定的目标属性。在我们的示例中，顶点着色器中 a_Position 是 vec2 类型，即每次接收两个数据，所以 size 设置为 2。以后我们绘制立体模型的时候，a_Position 会接收三个数据，size 相应地也会设置成 3。
    • type：数据类型，一般而言都是浮点型。
    • normalize：是否需要将非浮点类型数据单位化到【-1, 1】区间。
    • stride：步长，即每个顶点所包含数据的字节数，默认是 0 ，0 表示一个属性的数据是连续存放的。在我们的例子中，我们的一个顶点包含两个分量，X 坐标和 Y 坐标，每个分量都是一个 Float32 类型，占 4 个字节，所以，stride = 2 * 4 = 8 个字节。但我们的例子中，缓冲区只为一个属性a_Position服务，缓冲区的数据是连续存放的，因此我们可以使用默认值 0 来表示。但如果我们的缓冲区为多个属性所共用，那么 stride 就不能设置为 0 了，需要进行计算。
    • offset：在每个步长的数据里，目标属性需要偏移多少字节开始读取。在我们的例子中，buffer 只为 a_Position 一个属性服务，所以 offset 为 0 * 4 = 0。

假如我们的顶点数组为【10, 20, 30, 30, 40, 50, 60, 70】，每两个相邻数字代表一个顶点的 X 坐标和 Y 坐标。由于我们使用的是 Float32Array 浮点数组，每个数字占 4 个字节。

设置完变量和缓冲区的绑定之后，编写绘制代码：

//绘制图元设置为三角形
var primitiveType = gl.TRIANGLES;
//从顶点数组的开始位置取顶点数据
var offset = 0;
//因为我们要绘制三个点，所以执行三次顶点绘制操作。
var count = 3;
gl.drawArrays(primitiveType, offset, count);

img

动态绘制三角形​

到目前为止，我们已经实现了在屏幕上绘制一个固定三角形的功能，接下来我们实现动态绘制三角形，大家回想一下上节动态绘制点的逻辑，动态三角形的绘制和它基本类似。

着色器部分​

  • 顶点着色器增加一个变量用来接收 canvas 的尺寸，将 canvas 坐标转化为 NDC 坐标。
//设置浮点数精度为中等精度
precision mediump float;
// 接收顶点坐标 (x, y)
attribute vec2 a_Position;
// 接收 canvas 的尺寸(width, height)
attribute vec2 a_Screen_Size;
void main(){
    vec2 position = (a_Position / a_Screen_Size) * 2.0 - 1.0;
    position = position * vec2(1.0,-1.0);
    gl_Position = vec4(position, 0, 1);
}
  • 片元着色器部分没有改动。

JavaScript 部分​

在 JavaScript 代码部分，我们多了一些交互操作：

  • 鼠标点击 canvas，存储点击位置的坐标。
  • 每点击三次时，再执行绘制命令。因为三个顶点组成一个三角形，我们要保证当顶点个数是3的整数倍时，再执行绘制操作。

关键代码如下：

canvas.addEventListener('mouseup', e => {
    var x = e.pageX;
    var y = e.pageY;
    positions.push(x, y);
    if (positions.length % 6 == 0) {
      //向缓冲区中复制新的顶点数据。
        gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(positions), gl.DYNAMIC_DRAW);
        //重新渲染
        render(gl);
    }
})

//渲染函数
function render(gl) {
    gl.clearColor(0, 0, 0, 1.0);
    //用上一步设置的清空画布颜色清空画布。
    gl.clear(gl.COLOR_BUFFER_BIT);
    //绘制图元设置为三角形
    var primitiveType = gl.TRIANGLES;
    //从顶点数组的开始位置取顶点数据
    var drawOffset = 0;
    //因为我们要绘制 N 个点，所以执行 N 次顶点绘制操作。
    gl.drawArrays(primitiveType, 0, positions.length / 2);
}

总结​

  • 三角形图元分类
    • gl.TRIANGLES：基本三角形。
    • gl.TRIANGLE_STRIP：三角带。
    • gl.TRIANGLE_FAN：三角扇。
  • 类型化数组的作用。
    • Float32Array：32位浮点数组。
  • 使用缓冲区传递数据。
    • gl.createBuffer：创建buffer。
    • gl.bindBuffer：绑定某个缓冲区对象为当前缓冲区。
    • gl.bufferData：往缓冲区中复制数据。
    • gl.enableVertexAttribArray：启用顶点属性。
    • gl.vertexAttribPointer：设置顶点属性从缓冲区中读取数据的方式。
  • 动态绘制三角形。
    • 改变顶点信息，然后通过缓冲区将改变后的顶点信息传递到着色器，重新绘制三角形。

动态绘制线段(点击动态绘制线段)​

线段图元分类​

线段图元分为三种：

  • LINES：基本线段。
  • LINE_STRIP：带状线段。
  • LINE_LOOP：环状线段。

LINES 图元​

LINES 图元称为基本线段图元，绘制每一条线段都需要明确指定构成线段的两个端点。

我们还是通过每次点击产生一个点，并将点击位置坐标放进 positions 数组中。

注意，我们的坐标还是相对于屏幕坐标系，顶点着色器中会将屏幕坐标系转换到裁剪坐标系，也就是坐标区间在[-1, 1]之间。

var positions = [];
canvas.addEventListener('mouseup', e => {
    var x = e.pageX;
    var y = e.pageY;
    positions.push(x);
    positions.push(y);
    if (positions.length > 0) {
        gl.bufferData(
        gl.ARRAY_BUFFER,
        new Float32Array(positions),
        gl.DYNAMIC_DRAW
    );
        render(gl);
    }
});

之后进行绘制，注意执行 drawArrays 时，图元参数应该设置为 gl.LINES。

gl.drawArrays(gl.LINES, 0, positions.length / 2);

img

可以看到，每次点击两次之后才能绘制一条新的线段，也就是说，采用 gl.LINES 进行绘制的话，必须制定两个端点坐标。

LINE_STRIP​

LINE_STRIP 图元的绘制特点和 LINES 的有所区别，在绘制线段时，它会采用前一个顶点作为当前线段的起始端点。我们还是通过一个例子理解一下。

依然采用上面的代码，只不过这次在绘制时，将图元设置为 LINE_STRIP：

gl.drawArrays(gl.LINE_STRIP, 0, positions.length/2);

img

可以看到，除了第一条线段需要指定两个端点，之后每次点击一个新的点，都会自动绘制一条新线段，新线段的起点是上一个线段的终点。

LINE_LOOP​

顾名思义，环状线段除了包含 LINE_STRIP 的绘制特性，还有一个特点就是将线段的终点和第一个线段的起点进行连接，形成一个线段闭环。

废话不多说，看下效果大家就明白了。

gl.drawArrays(gl.LINE_LOOP, 0, positions.length/2);

img

绘制渐变三角形​

渐变三角形颜色不单一，在顶点与顶点之间进行颜色的渐变过渡，这就要求我们的顶点信息除了包含坐标，还要包含颜色。这样在顶点着色器之后，GPU 根据每个顶点的颜色对顶点与顶点之间的颜色进行插值，自动填补顶点之间像素的颜色，于是形成了渐变三角形。

需要为每个顶点传递坐标信息和颜色信息，因此需要在顶点着色器中额外增加一个 attribute 变量a_Color，用来接收顶点的颜色，同时还需要在顶点着色器和片元着色器中定义一个 varying 类型的变量v_Color，用来传递顶点颜色信息

着色器​

  • 依然从顶点着色器开始，顶点着色器新增一个 attribute 变量，用来接收顶点颜色。
    //设置浮点数精度为中等精度。
    precision mediump float;
    //接收顶点坐标 (x, y)
    attribute vec2 a_Position;
    //接收浏览器窗口尺寸(width, height)
    attribute vec2 a_Screen_Size;
    //接收 JavaScript 传递的顶点颜色
    attribute vec4 a_Color;
    //传往片元着色器的颜色。
    varying vec4 v_Color;
    void main(){
      vec2 position = (a_Position / a_Screen_Size) * 2.0 - 1.0;
      position = position * vec2(1.0,-1.0);
      gl_Position = vec4(position, 0, 1);
      v_Color = a_Color;
    }
  • 片元着色器

片元着色器新增一个 varying 变量 v_Color，用来接收插值后的颜色。

    //设置浮点数精度为中等。
    precision mediump float;
    //接收 JavaScript 传过来的颜色值（rgba）。
    varying vec4 v_Color;
    void main(){
      vec4 color = v_Color / vec4(255, 255, 255, 1);
      gl_FragColor = color;
   }

着色器部分还是和之前一样简，只是在顶点着色器中增加了顶点颜色这一变量。

JavaScript 部分​

用缓冲区向着色器传递数据有两种方式：

  • 利用一个缓冲区传递多种数据。
  • 另一种是利用多个缓冲区传递多个数据。

上节绘制三角形的时候我们给顶点着色器传递的只是坐标信息，并且只用了一个 buffer，本节示例，我们除了传递顶点的坐标数据，还要传递顶点颜色。 按照正常思路，我们可以创建两个 buffer，其中一个 buffer 传递坐标，另外一个 buffer 传递颜色。

img

创建两个 buffer，将 a_Position 和 positionBuffer 绑定，a_Color 和 colorBuffer 绑定，然后设置各自读取 buffer 的方式。

谨记：程序中如果有多个 buffer 的时候，在切换 buffer 进行操作时，一定要通过调用 gl.bindBuffer 将要操作的 buffer 绑定到 gl.ARRAY_BUFFER 上，这样才能正确地操作 buffer 。您可以将 bindBuffer 理解为一个状态机，bindBuffer 之后的对 buffer 的一些操作，都是基于最近一次绑定的 buffer 来进行的。

buffer 的操作需要在绑定 buffer 之后进行：

  • gl.bufferData：传递数据。
  • gl.vertexAttribPointer：设置属性读取 buffer 的方式

多个 buffer 传递传递信息​

我们使用一个 buffer 传递坐标信息，另一个 buffer 传递颜色信息。

// 创建 坐标信息 buffer
var positionBuffer = gl.createBuffer();
// 将当前 buffer 设置为 postionBuffer，接下来对 buffer 的操作都是针对 positionBuffer 了。
gl.bindBuffer(gl.ARRAY_BUFFER, positionBuffer);
// 设置 a_Position 变量读取 positionBuffer 缓冲区的方式。
var size = 2;
var type = gl.FLOAT;
var normalize = false;
var stride = 0;
var offset = 0;
gl.vertexAttribPointer(
      a_Position, size, type, normalize, stride, offset);
      
// 创建 颜色信息 buffer
var colorBuffer = gl.createBuffer();
// 将当前 buffer 设置为 postionBuffer，接下来对 buffer 的操作都是针对 positionBuffer 了。
gl.bindBuffer(gl.ARRAY_BUFFER, colorBuffer);
// 设置 a_Position 变量读取 positionBuffer 缓冲区的方式。
var size = 4;
var type = gl.FLOAT;
var normalize = false;
var stride = 0;
var offset = 0;
gl.vertexAttribPointer(
      a_Color, size, type, normalize, stride, offset);

我们发现，上面代码对 buffer 的操作有些冗余，我们还是提取出一个方法 createBuffer 放到 webgl-helper.js，减少重复编码，之后我们对 buffer 的一系列调用只需要如下两句就可以了：

var positionBuffer = createBuffer(gl, a_Position, { size: 2});
var colorBuffer = createBuffer(gl, a_Color, { size: 4});

假如我们顶点坐标数组中有四个顶点 8 个元素【30, 30, 30, 40, 40, 30, 20, 0】，顶点着色器中的 a_Position 属性在读取顶点坐标信息时，以 2 个元素为一组进行读取：

img

又假如我们顶点颜色数组中有两个顶点 8 个元素 【244, 230, 100, 1, 125, 30, 206, 1】，那么顶点着色器中的 a_Color 属性在读取顶点颜色信息时，以 4 个元素（r, g, b, a）为一组进行读取，如下图所示。

img

以多少元素作为一个顶点信息进行读取的设置，是在调用 gl.vertexAttribPointer 时设置的 size 参数值。

言归正传，接下来我们为 canvas 添加点击事件：

canvas.addEventListener('click', e => {
    var x = e.pageX;
    var y = e.pageY;
    positions.push(x, y);
    //随机一种颜色
    var color = randomColor();
    //将随机颜色的 rgba 值添加到顶点的颜色数组中。
    colors.push(color.r, color.g, color.b, color.a);
    //顶点的数量是 3 的整数倍时，执行绘制操作。
    if (positions.length % 6 == 0) {
        gl.bindBuffer(gl.ARRAY_BUFFER, buffer);
        gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(positions), gl.DYNAMIC_DRAW);
        gl.bindBuffer(gl.ARRAY_BUFFER, colorBuffer);
        gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(colors), gl.DYNAMIC_DRAW);
        render(gl);
    }
})

绘制：

    function render(gl) {
      //用设置的清空画布颜色清空画布。
      gl.clear(gl.COLOR_BUFFER_BIT);
      if (positions.length <= 0) {
        return;
      }
      //绘制图元设置为三角形。
      var primitiveType = gl.TRIANGLES;
      //因为我们要绘制三个点，所以执行三次顶点绘制操作。
      gl.drawArrays(primitiveType, 0, positions.length / 2);
    }

使用 1 个 buffer 同时传递坐标和颜色信息​

常规思路使用多个 buffer 传递多种数据（坐标和颜色），我们再演示另外一种思路：使用 1 个 buffer 同时传递多种数据。

着色器部分的代码和上面的一样，无需改动，改动的主要部分是 JavaScript 程序。

首先，我们依然是创建 buffer，只不过这次是创建一个 buffer。

var buffer = gl.createBuffer();
gl.bindBuffer(gl.ARRAY_BUFFER, buffer);

创建完 buffer，接下来设置读取 buffer 的方式，我们有两个属性 a_Position、a_Color，由于我们只有一个 buffer，该 buffer 中既存储坐标信息，又存储颜色信息，所以两个属性需要读取同一个 buffer：

image-20220727094242012

我们可以看到，一个顶点信息占用 6 个元素，前两个元素代表坐标信息，后四个元素代表颜色信息，所以在下面设置属性读取 buffer 方式时，a_Color 和 a_Position 的设置会有不同：

  • a_Position：坐标信息占用 2 个元素，故 size 设置为 2。 坐标信息是从第一个元素开始读取，偏移值为 0 ，所以 offset 设置为 0.
  • a_Color：由于 color 信息占用 4 个元素，所以 size 设置为 4 。 color 信息是在坐标信息之后，偏移两个元素所占的字节（2 * 4 = 8）。所以，offset 设置为 8。
  • stride：代表一个顶点信息所占用的字节数，我们的示例，一个顶点占用 6 个元素，每个元素占用 4 字节，所以，stride = 4 * 6 = 24 个字节。
gl.vertexAttribPointer(
      a_Color, 4, gl.FLOAT, false, 24, 8);
      
gl.vertexAttribPointer(
      a_Position, 2, gl.FLOAT, false, 24, 0);

canvas 的点击事件也有所不同，一个顶点占用 6 个元素，三个顶点组成一个三角形，所以我们的 positions 的元素数量必须是 18 的整数倍，才能组成一个三角形：

    canvas.addEventListener('click', e => {
      var x = e.pageX;
      var y = e.pageY;
      positions.push(x);
      positions.push(y);
      //随机出一种颜色
      var color = randomColor();
      //将随机颜色的 rgba 值添加到顶点的颜色数组中。
      positions.push(color.r, color.g, color.b, color.a);
      //顶点的数量是 18 的整数倍时，执行绘制操作。
      if (positions.length % 18 == 0) {
        gl.bufferData(gl.ARRAY_BUFFER, new Float32Array(positions), gl.STATIC_DRAW);
        render(gl);
      }
    })

实现效果和上面操作多缓冲区的方式一样，但是单缓冲区不仅减少了缓冲区的数量，而且减少了传递数据的次数以及复杂度。

绘制矩形​

基本三角形构建矩形​

一个矩形其实可以由两个共线的三角形组成，即 V0, V1, V2, V3，其中 V0 -> V1 -> V2 代表三角形A，V0 -> V2 -> V3代表三角形B。

组成三角形的顶点要按照一定的顺序绘制。默认情况下，WebGL 会认为顶点顺序为逆时针时代表正面，反之则是背面，区分正面、背面的目的在于，如果开启了背面剔除功能的话，背面是不会被绘制的。当我们绘制 3D 形体的时候，这个设置很重要。

着色器​

  • 顶点着色器
    • a_Position
    • a_Color
    • a_Screen_Size
    • v_Color
  • 片元着色器
    • v_Color

JavaScript代码​

绘制固定顶点的矩形。

首先准备组成矩形的三角形，每个三角形由三个顶点组成，两个矩形共需要六个顶点。

var positions = [
    30, 30, 255, 0, 0, 1,    //V0
    30, 300, 255, 0, 0, 1,   //V1
    300, 300, 255, 0, 0, 1,  //V2
    30, 30, 0, 255, 0, 1,    //V0
    300, 300, 0, 255, 0, 1,  //V2
    300, 30, 0, 255, 0, 1    //V3
]

我们给两个三角形设置不同颜色，其中，V0->V1->V2 三角形设置为红色， VO->V2->V3 三角形设置为绿色

img

索引方式绘制​

我们在绘制一个矩形的时候，实际上只需要 V0, V1, V2, V3 四个顶点即可，可是我们却存储了六个顶点，每个顶点占据 4 6 = 24 个字节，绘制一个简单的矩形我们就浪费了 24 2 = 48 字节的空间，那真正的 WebGL 应用都是由成百上千个，甚至几十万、上百万个顶点组成，这个时候，重复的顶点信息所造成的内存浪费就不容小觑了

WebGL 除了提供 gl.drawArrays 按顶点绘制的方式以外，还提供了一种按照顶点索引进行绘制的方法：gl.drawElements，使用这种方式，可以避免重复定义顶点，进而节省存储空间

gl.drawElements 的使用方法

void gl.drawElements(mode, count, type, offset);

  • mode：指定绘制图元的类型，是画点，还是画线，或者是画三角形。
  • count：指定绘制图形的顶点个数。
  • type：指定索引缓冲区中的值的类型,常用的两个值：gl.UNSIGNED_BYTE和gl.UNSIGNED_SHORT，前者为无符号8位整数值，后者为无符号16位整数。
  • offset：指定索引数组中开始绘制的位置，以字节为单位。

例子

gl.drawElements(gl.TRIANGLES, 3, gl.UNSIGNED_BYTE, 0);

解释

采用三角形图元进行绘制，共绘制 3 个顶点，顶点索引类型是 gl.UNSIGNED_BYTE，从顶点索引数组的开始位置绘制

使用 drawElements 绘制矩形​

JavaScript代码​

采用索引绘制方式，我们除了准备存储顶点信息的数组，还要准备存储顶点索引的数组

//存储顶点信息的数组
var positions = [
    30, 30, 255, 0, 0, 1,    //V0
    30, 300, 255, 0, 0, 1,   //V1
    300, 300, 255, 0, 0, 1,  //V2
    300, 30, 0, 255, 0, 1    //V3
];
//存储顶点索引的数组
var indices = [
    0, 1, 2, //第一个三角形
    0, 2, 3  //第二个三角形
];

除了多准备一个数组容器存储顶点索引以外，我们还需要将索引传递给 GPU，所以，仍然需要创建一个索引 buffer.

var indicesBuffer = gl.createBuffer();

按照惯例，创建完 buffer，我们需要绑定，这里要和 ARRAY_BUFFER 区分开来，索引 buffer 的绑定点是gl.ELEMENT_ARRAY_BUFFER。

gl.bindBuffer(gl.ELEMENT_ARRAY_BUFFER, indicesBuffer);

接下来，我们就可以往 indicesBuffer 中传入顶点索引了：

gl.bufferData(gl.ELEMENT_ARRAY_BUFFER, new Uint16Array(indices), gl.STATIC_DRAW);

之后执行绘制操作：

gl.drawElements(gl.TRIANGLES, 6, gl.UNSIGNED_SHORT, 0);

img

我们用 drawArrays 进行绘制的时候，使用了六个顶点，每个三角形的顶点颜色一致，所以两个三角形的颜色都是单一的。 当采用 drawElements 方法进行绘制的时候，使用了四个顶点，第二个三角形的两个顶点 V0、V2 是红色的，第三个顶点 V3 是绿色的，所以造成了从 V0、V2 向 V3 的红绿渐变

使用三角带构建矩形​

三角带的绘制特点是前后两个三角形是共线的，并且我们知道顶点数量与绘制的三角形的数量之间的关系是：

顶点数或者索引数 = 三角形数量 + 2

仍然以绘制矩形为目标，如果采用基本三角形进行绘制的话，需要准备六个顶点，即两个三角形。那如果采用三角带进行绘制的话，利用三角带的特性，我们实际需要的顶点数为 2 + 2 = 4，即矩形的四个顶点位置。

img

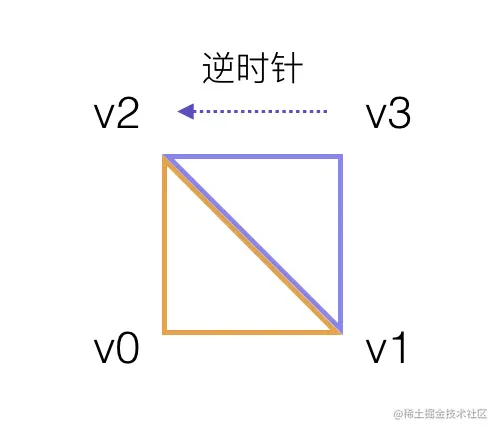
绘制三角带图元的时候，V0->V1->V2 组成第一个三角形，V2->V1->V3 组成第二个三角形

三角带与基本三角形绘制在代码上的区别有两点：

  • 顶点数组的数据不同。
  • drawArrays 的第一个参数代表的图元类型不同。
    • 基本三角形：TRIANGLES。
    • 三角带：TRIANGLE_STRIP。
    • 三角扇：TRIANGLE_FAN。

关键代码​

顶点数组：

var positions = [
    30, 300, 255, 0, 0, 1,   //V0  
    300, 300, 255, 0, 0, 1,  //V1
    30, 30, 255, 0, 0, 1,    //V2
    300, 30, 0, 255, 0, 1    //V3
]

绘制方法：

gl.drawArrays(gl.TRIANGLE_STRIP, 0, );

如果V1->V2->V0 绘制第一个三角形，V0->V2->V3绘制第二个三角形

var positions = [
   300, 300, 255, 0, 0, 1,  //V1
   30, 30, 255, 0, 0, 1,    //V2
   30, 300, 255, 0, 0, 1,   //V0
   300, 30, 0, 255, 0, 1    //V3
]

img

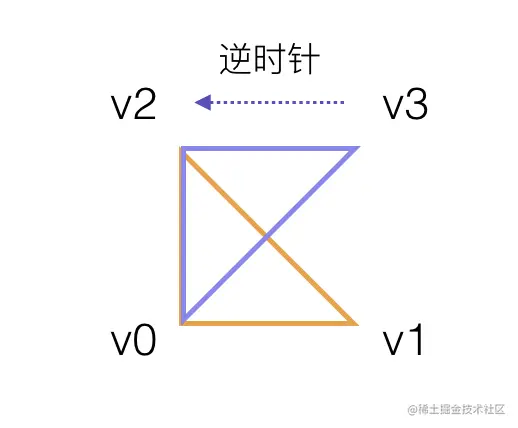
三角扇绘制矩形​

三角扇是围绕着第一个顶点作为公共顶点绘制三角形的，并且使用三角扇绘制出来的三角形的数量和顶点数量之间的关系和三角带一样：

顶点数或者索引数 = 三角形数量 + 2

img

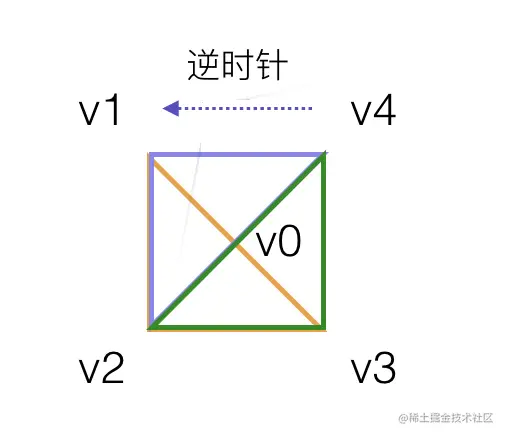
使用三角扇需要绘制 4 个三角形，相应地顶点数量为 6 个：

三角形顶点组成
左边三角形V0 -> V1 -> V2
上边三角形V0 -> V2 -> V3
右边三角形V0 -> V3 -> V4
下边三角形V0 -> V4 -> V1

需要的顶点数组为

var positions = [
    165, 165, 255, 255, 0, 1, //V0
    30, 30, 255, 0, 0, 1,    //V1
    30, 300, 255, 0, 0, 1,   //V2
    300, 300, 255, 0, 0, 1,  //V3
    300, 30, 0, 255, 0, 1,   //V4
    30, 30, 255, 0, 0, 1,    //V1
]

绘制方式改为三角扇：

gl.drawArrays(gl.TRIANGLE_FAN, 0, positions.length / 6);

四个三角形都以中心点为顶点

img

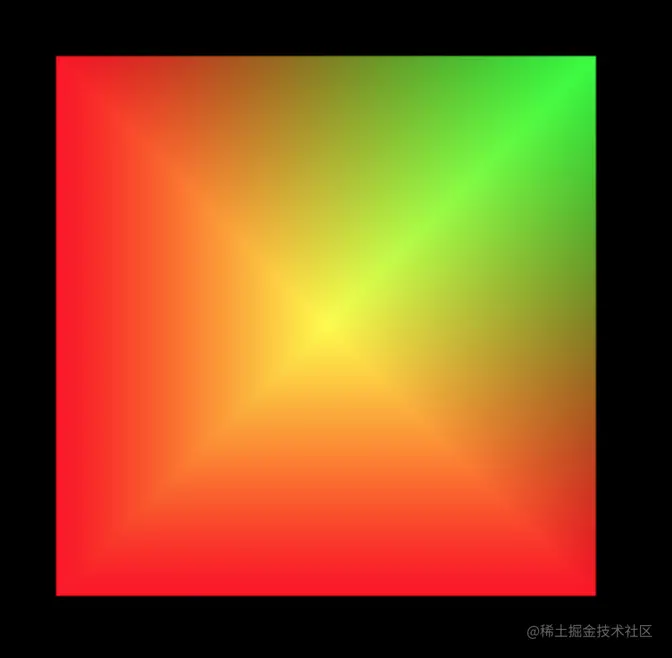
绘制圆形​

将圆形分割成以圆心为共同顶点的若干个三角形，三角形数越多，圆形越平滑。

img

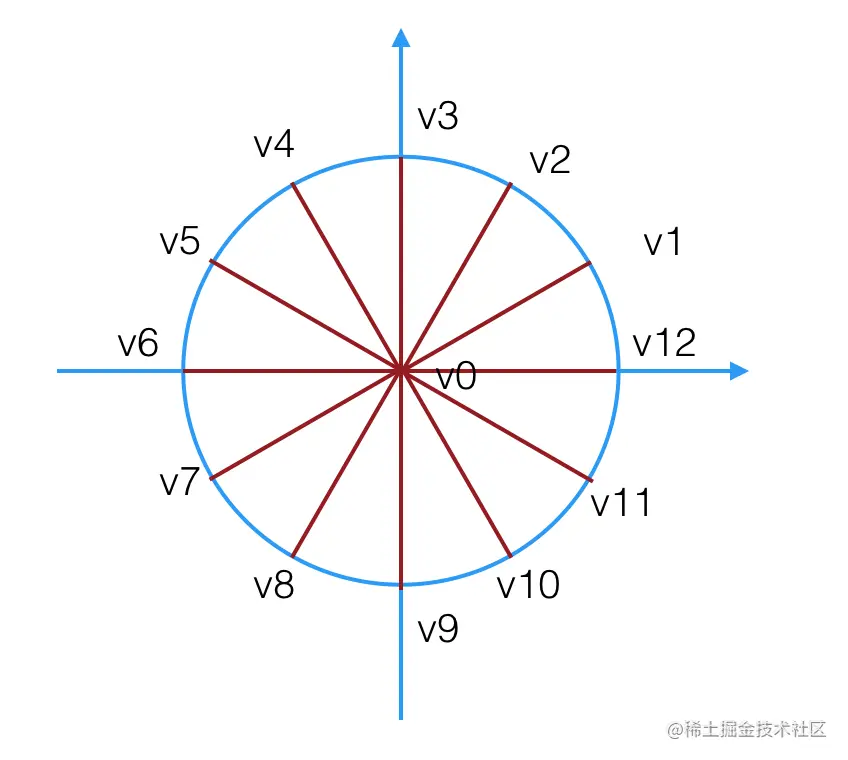
将圆形划分成 12 个三角形，13 个顶点，我们需要计算每个顶点的坐标，我们定义一个生成圆顶点的函数：

  • x：圆心的 x 坐标
  • y：圆心的 y 坐标
  • radius：半径
  • n：三角形的数量
    var sin = Math.sin;
    var cos = Math.cos;
    function createCircleVertex(x, y, radius, n) {
      var positions = [x, y, 255, 0, 0, 1];
      for (let i = 0; i <= n; i++) {
        var angle = i * Math.PI * 2 / n;
        positions.push(x + radius * sin(angle), y + radius * cos(angle), 255, 0, 0, 1);
      }
      return positions;
    }
   var positions = createCircleVertex(100, 100, 50,  12);

圆切分成 50 个三角形试试：

var positions = createCircleVertex(100, 100, 50,  50);

img

绘制环形​

img

建立两个圆，一个内圆，一个外圆，划分n个近似于扇形的三角形，每个三角形的两条边都会和内圆和外圆相交，产生四个交点，这四个交点组成一个近似矩形，然后将近似矩形划分成两个三角形：

function createRingVertex(x, y, innerRadius, outerRadius, n) {
    var positions = [];
    var color = randomColor();
    for (var i = 0; i <= n; i++) {
        if (i % 2 == 0) {
            color = randomColor();
        }
        var angle = i * Math.PI * 2 / n;
        positions.push(x + innerRadius * sin(angle), y + innerRadius * cos(angle), color.r, color.g, color.b, color.a);
        positions.push(x + outerRadius * sin(angle), y + outerRadius * cos(angle), color.r, color.g, color.b, color.a);
    }
    var indices = [];
    for (var i = 0; i < n; i++) {
        var p0 = i * 2;
        var p1 = i * 2 + 1;
        var p2 = (i + 1) * 2 + 1;
        var p3 = (i + 1) * 2;
        if (i == n - 1) {
          p2 = 1;
          p3 = 0;
        }
        indices.push(p0, p1, p2, p2, p3, p0);
    }
    return { 
        positions: positions, 
        indices: indices 
    };
}

上面这个方法能够根据内圆半径和外圆半径以及三角形的数量返回顶点数组和索引数组，我们生成 100 个三角形的信息。

var geo = createRingVertex(100, 100, 20, 50, 100);

为了节省空间，我们采用索引绘制：

gl.drawElements(gl[currentType], indices.length, gl.UNSIGNED_SHORT, 0);

效果如下：

img

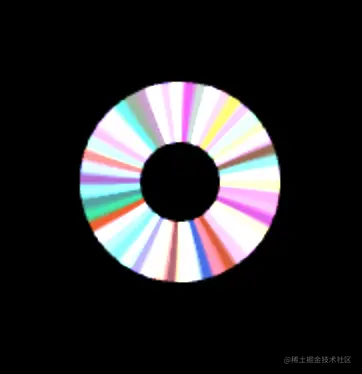
纹理贴图​

在实际的建模中（游戏居多），模型表面往往都是丰富生动的图片。这就需要有一种机制，能够让我们把图片素材渲染到模型的一个或者多个表面上，这种机制叫做纹理贴图

纹理图片格式​

WebGL 对图片素材是有严格要求的，图片的宽度和高度必须是 2 的 N 次幂，比如 16 x 16，32 x 32，64 x 64 等。实际上，不是这个尺寸的图片也能进行贴图，但是这样会使得贴图过程更复杂，从而影响性能，所以我们在提供图片素材的时候最好参照这个规范。

纹理坐标系统​

纹理也有一套自己的坐标系统，为了和顶点坐标加以区分，通常把纹理坐标称为 UV，U 代表横轴坐标，V 代表纵轴坐标。

  • 图片坐标系统的特点是：
    • 左上角为原点(0, 0)。
    • 向右为横轴正方向，横轴最大值为 1，即横轴坐标范围【1，0】。
    • 向下为纵轴正方向，纵轴最大值为 1，即纵轴坐标范围【0，1】。
  • 纹理坐标系统不同于图片坐标系统，它的特点是：
    • 左下角为原点(0, 0)。
    • 向右为横轴正方向，横轴最大值为 1，即横轴坐标范围【1，0】。
    • 向上为纵轴正方向，纵轴最大值为 1，即纵轴坐标范围【0，1】。

img

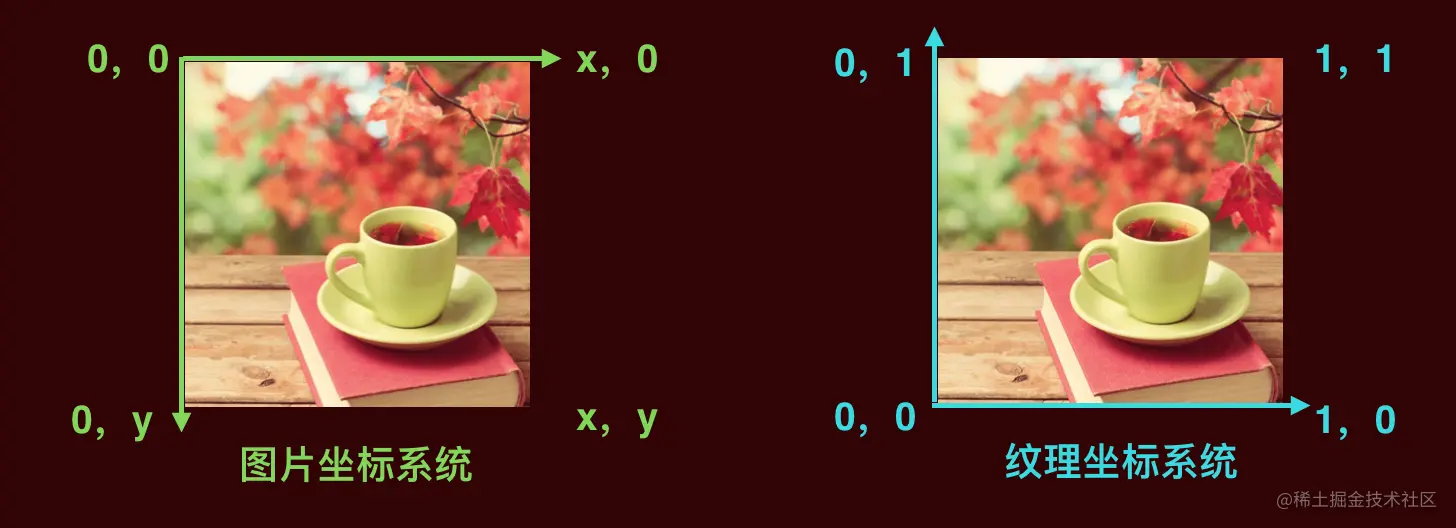
着色器​

片元着色器中，不再是接收单纯的颜色了，而是接收纹理图片对应坐标的颜色值，所以我们的着色器要能够做到如下几点：

  • 顶点着色器接收顶点的 UV 坐标，并将UV坐标传递给片元着色器。

  • 片元着色器要能够接收顶点插值后的UV坐标，同时能够在纹理资源找到对应坐标的颜色值。

  • 顶点着色器

首先，增加一个名为 v_Uv 的 attribute 变量，接收 JavaScript 传递过来的 UV 坐标。 其次，增加一个 varying 变量 v_Uv，将 UV 坐标插值化，并传递给片元着色器。

    precision mediump float;
   // 接收顶点坐标 (x, y)
   attribute vec2 a_Position;
   // 接收 canvas 尺寸(width, height)
   attribute vec2 a_Screen_Size;
   // 接收JavaScript传递过来的顶点 uv 坐标。
   attribute vec2 a_Uv;
   // 将接收的uv坐标传递给片元着色器
   varying vec2 v_Uv;
   void main(){
     vec2 position = (a_Position / a_Screen_Size) * 2.0 - 1.0;
     position = position * vec2(1.0,-1.0);
     gl_Position = vec4(position, 0, 1);
     // 将接收到的uv坐标传递给片元着色器
     v_Uv = a_Uv;
   }
  • 片元着色器 首先，增加一个 varying 变量 v_Uv，接收顶点着色器插值过来的 UV 坐标。 其次，增加一个 sampler2D 类型的全局变量 texture，用来接收 JavaScript 传递过来的纹理资源（图片数据）。
    precision mediump float;
    // 接收顶点着色器传递过来的 uv 值。
    varying vec2 v_Uv;
    // 接收 JavaScript 传递过来的纹理
    uniform sampler2D texture;
    void main(){
        // 提取纹理对应uv坐标上的颜色，赋值给当前片元（像素）。
        gl_FragColor = texture2D(texture, vec2(v_Uv.x, v_Uv.y));
    }

JavaScript​

我们首先要将纹理图片加载到内存中：

    var img = new Image();
    img.onload = textureLoadedCallback;
    img.src = "";

图片加载完成之后才能执行纹理的操作，我们将纹理操作放在图片加载完成后的回调函数中，即textureLoadedCallback。

需要注意的是，我们使用 canvas 读取图片数据是受浏览器跨域限制的，所以首先要解决跨域问题。

可以将图片资源和页面资源部署在同一域名下，这样就不存在跨域问题了

实际生产环境中，图片资源往往部署在 CDN 上，图片和页面分属不同域，这种情况的跨域访问我们就需要正面解决了。

假设我们的图片资源所属域名为：https://cdn-pic.com，页面所属域名为 https://test.com。

解决方法如下：

  • 首先：为图片资源设置跨域响应头：
Access-Control-Allow-Origin：`https://test.com`
  • 其次：在图片加载时，为 img 设置 crossOrigin 属性。
var img = new Image();
img.crossOrigin = '';
img.src = 'https://cdn-pic.com/test.jpg'

我们定义六个顶点，这六个顶点能够组成一个矩形，并为顶点指定纹理坐标。

    var positions = [
      30, 30, 0, 0,    //V0
      30, 300, 0, 1,   //V1
      300, 300, 1, 1,  //V2
      30, 30, 0, 0,    //V0
      300, 300, 1, 1,  //V2
      300, 30, 1, 0    //V3
    ]

加载图片

    var img  = new Image();
    img.onload = textureLoadedCallback;
    img.src=""

图片加载完成后，我们进行如下操作：

首先：激活 0 号纹理通道gl.TEXTURE0，0 号纹理通道是默认值，本例也可以不设置。

    gl.activeTexture(gl.TEXTURE0);

然后创建一个纹理对象：

    var texture = gl.createTexture();

之后将创建好的纹理对象texture绑定 到当前纹理绑定点上，即 gl.TEXTURE_2D。绑定完之后对当前纹理对象的所有操作，都将基于 texture 对象，直到重新绑定。

    gl.bindTexture(gl.TEXTURE_2D, texture);

为片元着色器传递图片数据：

gl.texImage2D(gl.TEXTURE_2D, 0, gl.RGBA, gl.RGBA, gl.UNSIGNED_BYTE, img);

gl.texImage2D 方法是一个重载方法，其中有一些参数可以省略：

glTexImage2D(GLenum target, GLint level, GLint components, GLsizei width, glsizei height, GLint border, GLenum format, GLenum type, const GLvoid *pixels);

参数含义
target纹理类型，TEXTURE_2D代表2维纹理
level表示多级分辨率的纹理图像的级数，若只有一种分辨率，则 level 设为 0，通常我们使用一种分辨率
components纹理通道数，通常我们使用 RGBA 和 RGB 两种通道
width纹理宽度，可省略
height纹理高度，可省略
border边框，通常设置为0，可省略
format纹理映射的格式
type纹理映射的数据类型
pixels纹理图像的数据

我们将 img 变量指向的图片数据传递给片元着色器，取对应纹理坐标的 RGBA 四个通道值，赋给片元，每个通道的数据格式是无符号单字节整数

设置图片在放大或者缩小时采用的算法gl.LINEAR。

gl.LINEAR 代表采用最靠近象素中心的四个象素的加权平均值，这种效果表现的更加平滑自然。 gl.NEAREST 采用最靠近象素中心的纹素，该算法可能使图像走样，但是执行效率高，不需要额外的计算。

gl.texParameterf(gl.TEXTURE_2D, gl.TEXTURE_MAG_FILTER, gl.LINEAR);
gl.texParameterf(gl.TEXTURE_2D, gl.TEXTURE_MIN_FILTER, gl.LINEAR);

之后为片元着色器传递 0 号纹理单元：

gl.uniform1i(uniformTexture, 0);

这里，我们为片元着色器的 texture 属性传递 0，此处应该与激活纹理时的通道值保持一致。

贴图原理​

只是指定了三角形的顶点对应的 UV 坐标，GPU 就能够将纹理图片的其他坐标的颜色贴到三角形表面呢？

在光栅化阶段，GPU 处理两件事情：

  • 计算图元覆盖了哪些像素。
  • 根据顶点着色器的顶点位置计算每个像素的纹理坐标的插值。

注：片元可以理解为像素。

光栅化结束后，来到片元着色器，片元着色器此时知道每个像素对应的 UV 坐标，根据当前像素的 UV 坐标，找到纹理资源对应坐标的颜色信息，赋值给当前像素，从而能够为图元表面的每个像素贴上正确的纹理颜色。

平面属性总结​

  • GLSL：着色器
    • 数据类型
      • vec2：2 维向量容器。
      • vec4：4 维向量容器。
      • 运算法则：向量与向量、向量与浮点数的运算法则。
    • 修饰符
      • attribute：属性修饰符。
      • uniform：全局变量修饰符。
      • varying：顶点着色器传递给片元着色器的属性修饰符。
    • precision：设置精度
      • highp：高精度。
      • mediump：中等精度。
      • lowp：低精度。
    • 内置变量
      • gl_Position：顶点坐标。
      • gl_FragColor：片元颜色。
      • gl_PointSize：顶点大小。
    • 屏幕坐标系到设备坐标系的转换。
      • 屏幕坐标系左上角为原点，X 轴坐标向右为正，Y 轴坐标向下为正。
      • 坐标范围：
        • X轴：【0, canvas.width】
        • Y轴：【0, canvas.height】
      • 设备坐标系以屏幕中心为原点，X 轴坐标向右为正，Y 轴向上为正。
      • 坐标范围是
        • X轴：【-1, 1】。
        • Y轴：【-1, 1】。
  • WebGL API
    • shader：着色器对象
      • gl.createShader：创建着色器。
      • gl.shaderSource：指定着色器源码。
      • gl.compileShader：编译着色器。
    • program：着色器程序
      • gl.createProgram：创建着色器程序。
      • gl.attachShader：链接着色器对象。
      • gl.linkProgram：链接着色器程序。
      • gl.useProgram：使用着色器程序。
    • attribute：着色器属性
      • gl.getAttribLocation：获取顶点着色器中的属性位置。
      • gl.enableVertexAttribArray：启用着色器属性。
      • gl.vertexAttribPointer：设置着色器属性读取 buffer 的方式。
      • gl.vertexAttrib2f：给着色器属性赋值，值为两个浮点数。
      • gl.vertexAttrib3f：给着色器属性赋值，值为三个浮点数。
    • uniform：着色器全局属性
      • gl.getUniformLocation：获取全局变量位置。
      • gl.uniform4f：给全局变量赋值 4 个浮点数。
      • gl.uniform1i：给全局变量赋值 1 个整数。
    • buffer：缓冲区
      • gl.createBuffer：创建缓冲区对象。
      • gl.bindBuffer：将缓冲区对象设置为当前缓冲。
      • gl.bufferData：向当前缓冲对象复制数据。
    • clear：清屏
      • gl.clearColor：设置清除屏幕的背景色。
      • gl.clear：清除屏幕。
    • draw：绘制
      • gl.drawArrays：数组绘制方式。
      • gl.drawElements：索引绘制方式。
    • 图元
      • gl.POINTS：点。
      • gl.LINE：基本线段。
      • gl.LINE_STRIP：连续线段。
      • gl.LINE_LOOP：闭合线段。
      • gl.TRIANGLES：基本三角形。
      • gl.TRIANGLE_STRIP：三角带。
      • gl.TRIANGLE_FAN：三角扇。
    • 纹理
      • gl.createTexture：创建纹理对象。
      • gl.activeTexture：激活纹理单元。
      • gl.bindTexture：绑定纹理对象到当前纹理。
      • gl.texImage2D：将图片数据传递给 GPU。
      • gl.texParameterf：设置图片放大缩小时的过滤算法。

绘制立方体​

WebGL 坐标系​

3D 形体的顶点坐标需要包含深度信息 Z 轴 坐标

WebGL 采用左手坐标系，X 轴向右为正，Y 轴向上为正，Z 轴沿着屏幕往里为正，如下图：

img

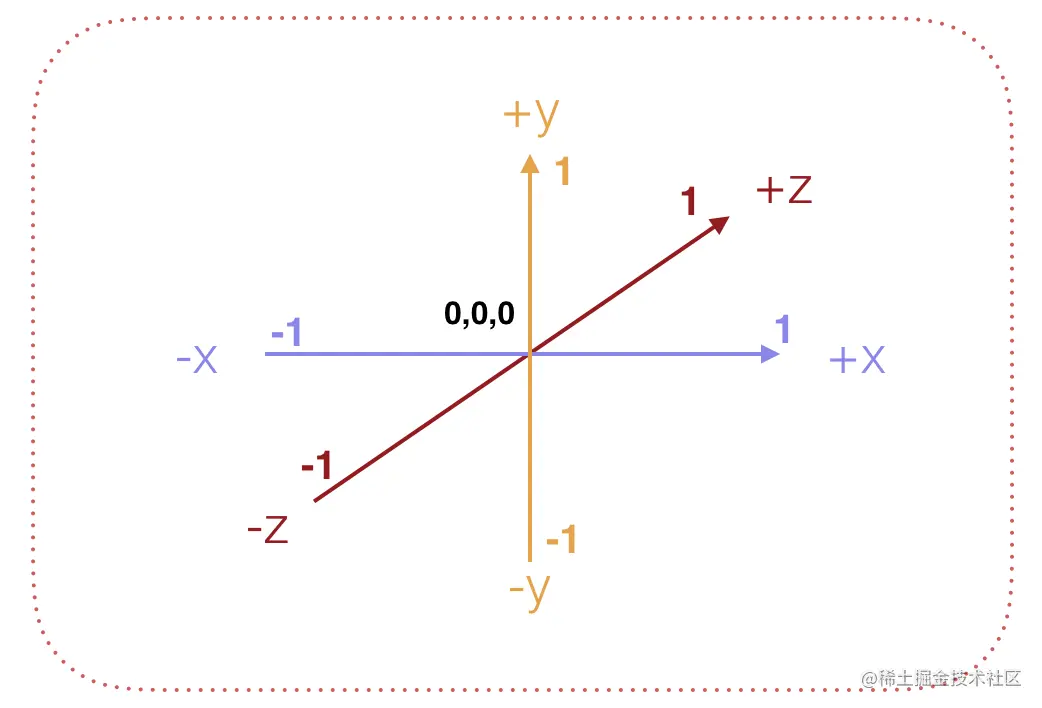
WebGL 是遵循右手坐标系，但仅仅是遵循，是期望大家遵守的规范。其实 WebGL 内部 (裁剪坐标系) 是基于左手坐标系的，Z 轴沿屏幕向里为正方向

WebGL 坐标系 X、Y、Z 三个坐标分量的的范围是【-1，1】，即一个边长为 2 的正方体，原点在正方体中心。我们称这个坐标系为标准设备坐标系，简称 NDC 坐标系。

大家应该还记得，前面章节我们经常在顶点着色器中使用内置属性 gl_Position，并且在为 gl_Position 赋值之前做了一些坐标系转换（屏幕坐标系转换到裁剪坐标系）操作。

为了理解 gl_Position 接收坐标前所做的变换目的，这就需要理解 gl_Position 接收什么样的坐标。

gl_Position 接收一个 4 维浮点向量，该向量代表的是裁剪坐标系的坐标。gl_Position 接收的坐标范围是顶点在裁剪坐标系中的坐标。

裁剪坐标系中的坐标通常由四个分量表示：(x, y, z, w)。请注意，w 分量代表齐次坐标分量，在之前的例子中，w 都是设置成 1 ，这样做的目的是让裁剪坐标系和 NDC 坐标系就保持一致，省去裁剪坐标到 NDC 坐标的转换过程。

gl_Position 接收到裁剪坐标之后，顶点着色器会对坐标进行透视除法，透视除法的公式是 (x/w, y/w, z/w, w/w) ，透视除法过后，顶点在裁剪坐标系中的坐标就会变成 NDC 坐标系中的坐标，各个坐标的取值范围将被限制在【-1，1】之间，如果某个坐标超出这个范围，将会被 GPU 丢弃。

透视除法这个步骤是顶点着色器程序黑盒执行的，对开发者来说是透明的，无法通过编程手段干预。但是我们需要明白有这么一个过程存在。

顶点坐标基于屏幕坐标系，然后在顶点着色器中对顶点作简单转换处理，转变成 NDC 坐标。

如何用三角形构建正方体​

一个只包含坐标信息的立方体实际上是由 6 个正方形，每个正方形由两个三角形组成，每个三角形由三个顶点组成，所以一个立方体由 6 个正方形 2 个三角形 3 个顶点 = 36 个顶点组成，但是这 36个顶点中有很多是重复的，我们很容易发现：一个纯色立方体实际上由 6 个矩形面，或者 8 个不重复的顶点组成。

请谨记，顶点的重复与否，不只取决于顶点的坐标信息一致，还取决于该顶点所包含的其他信息是否一致。比如顶点纹理坐标 uv、顶点法线，顶点颜色等。一旦有一个信息不同，就必须用两个顶点来表示。

以矩形举例，每个顶点只包含坐标和颜色两类信息

//顶点信息
var positions = [
    30, 30, 1, 0, 0, 1,    //V0
    30, 300, 1, 0, 0, 1,   //V1
    300, 300, 1, 0, 0, 1,  //V2
    30, 30, 1, 0, 0, 1,    //V0
    300, 300, 1, 0, 0, 1,  //V2
    300, 30, 1, 0, 0, 1    //V3
]

重复顶点的定义：两个顶点必须是所有信息一致，才可以称之为重复顶点。

彩色立方体​

立方体是 3 维形体，所以它们的顶点坐标需要从 2 维扩展成 3 维，除了 x、y 坐标，还需要深度值： z 轴坐标。

  • 顶点属性不再使用一个 buffer 混合存储，改为每个属性对应一个 buffer，便于维护。

  • 顶点坐标我们不再使用屏幕坐标系，而是采用 NDC 坐标系

  • 定义顶点

  • 传递数据

  • 执行绘制。

首先定义顶点，由于立方体包含六个面，每个面采用同一个颜色，所以我们需要定义 6 个矩形面 * 4 个顶点 = 24 个不重复的顶点。

    //正方体 8 个顶点的坐标信息
let zeroX = 0.5;
let zeroY = 0.5;
let zeroZ = 0.5;
let positions = [
    [-zeroX, -zeroY, zeroZ],  //V0
    [zeroX, -zeroY, zeroZ],  //V1
    [zeroX, zeroY, zeroZ],   //V2
    [-zeroX, zeroY, zeroZ],  //V3
    [-zeroX, -zeroY, -zeroZ],//V4
    [-zeroX, zeroY, -zeroZ], //V5
    [zeroX, zeroY, -zeroZ],  //V6
    [zeroX, -zeroY, -zeroZ]  //V7
]

接下来定义六个面包含的顶点索引：

const CUBE_FACE_INDICES = [
  [0, 1, 2, 3], //前面
  [4, 5, 6, 7], //后面
  [0, 3, 5, 4], //左面
  [1, 7, 6, 2], //右面
  [3, 2, 6, 5], //上面
  [0, 4, 7, 1] // 下面
];

定义六个面的颜色信息：

const FACE_COLORS = [
    [1, 0, 0, 1], // 前面，红色
    [0, 1, 0, 1], // 后面，绿色
    [0, 0, 1, 1], // 左面，蓝色
    [1, 1, 0, 1], // 右面，黄色
    [1, 0, 1, 1], // 上面，品色
    [0, 1, 1, 1]  // 下面，青色
]

有了顶点坐标和颜色信息，接下来我们写一个方法生成立方体的顶点属性。 该方法接收三个参数：宽度、高度、深度，返回一个包含组成立方体的顶点坐标、颜色、索引的对象。

function createCube(width, height, depth) {
  let zeroX = width / 2;
  let zeroY = height / 2;
  let zeroZ = depth / 2;

  let cornerPositions = [
    [-zeroX, -zeroY, -zeroZ],
    [zeroX, -zeroY, -zeroZ],
    [zeroX, zeroY, -zeroZ],
    [-zeroX, zeroY, -zeroZ],
    [-zeroX, -zeroY, zeroZ],
    [-zeroX, zeroY, zeroZ],
    [zeroX, zeroY, zeroZ],
    [zeroX, -zeroY, zeroZ]
  ];
  let colorInput = [
    [255, 0, 0, 1],
    [0, 255, 0, 1],
    [0, 0, 255, 1],
    [255, 255, 0, 1],
    [0, 255, 255, 1],
    [255, 0, 255, 1]
  ];

  let colors = [];
  let positions = [];
  var indices = [];

  for (let f = 0; f < 6; ++f) {
    let faceIndices = CUBE_FACE_INDICES[f];
    let color = colorInput[f];
    for (let v = 0; v < 4; ++v) {
      let position = cornerPositions[faceIndices[v]];
      positions = positions.concat(position);
      colors = colors.concat(color);
    }
    let offset = 4 * f;
    indices.push(offset + 0, offset + 1, offset + 2);
    indices.push(offset + 0, offset + 2, offset + 3);
  }
  indices = new Uint16Array(indices);
  positions = new Float32Array(positions);
  colors = new Float32Array(colors);
  return {
    positions: positions,
    indices: indices,
    colors: colors
  };
}

有了生成立方体顶点的方法，我们生成一个边长为 1 的正方体：

var cube = createCube(1, 1, 1);

拿到了顶点的信息，就可以用我们熟悉的索引绘制方法来进行绘制了，这部分代码和之前一样，我们就不写了，看下效果：

img

为什么显示的是长方形？

我们给 gl_Position 赋的坐标，在 渲染到屏幕之前，GPU 还会对其做一次坐标变换：视口变换。该变换会将 NDC 坐标转换成对应设备的视口坐标。

假设有一顶点 P（0.5，0.5，0.5，1）， gl_Position 接收到坐标后，会经历如下阶段：

  • 首先执行透视除法，将顶点 P 的坐标从裁剪坐标系转换到 NDC 坐标系，转换后的坐标为： P1（0.5 / 1, 0.5 / 1, 0.5 / 1, 1 / 1）。由于 w 分量是 1， 所以 P1 和 P 的坐标一致。
  • 接着，GPU 将顶点渲染到屏幕之前，对顶点坐标执行视口变换。假设我们的 canvas 视口宽度 300，高度 400，顶点坐标在 canvas 中心。那么 3D 坐标转换成 canvas 坐标的算法是:
  • canvas 坐标系 X 轴坐标 = NDC 坐标系下 X 轴坐标 300 / 2 = 0.5 150 = 75
  • canvas 坐标系 Y 轴坐标 = NDC 坐标系下 Y 轴坐标 400 / 2 = 0.5 200 = 100

所以会有一个问题，立方体的每个面宽度和高度虽然都是 1 ，但是渲染效果会随着显示设备的尺寸不同而不同

需要进行投影变换

如何看到立方体的其他表面？

因为我们绘制的是立方体，没有施加动画效果，所以我们只能看到立方体前表面 需要进行模型变换

每个转换可以用一个矩阵来表示，转换矩阵相乘，得出的最终矩阵用来表示组合变换

让立方体转动起来

  • 引入模型变换让立方体可以转动，以便我们能观察其他表面。
  • 引入投影变换让我们的正方体能够以正常比例渲染到目标设备，不再随视口的变化而拉伸失真。

为了引入这两个变换，我们需要引入矩阵乘法、绕 X 轴旋转、绕 Y 轴旋转、正交投影四个方法，如下：

//返回一个单位矩阵
function identity() {}
//计算两个矩阵的乘积，返回新的矩阵。
function multiply(matrixLeft, matrixRight){}
//绕 X 轴旋转一定角度，返回新的矩阵。
function rotationX(angle) {}
//绕 Y 轴旋转一定角度，返回新的矩阵。
function rotateY(m, angle) {}
//正交投影，返回新的矩阵
function ortho(left, right, bottom, top, near, far, target) {}

在顶点着色器中定义一个变换矩阵，用来接收 JavaScript 中传过来的模型投影变换矩阵，同时将变换矩阵左乘顶点坐标。

    // 接收顶点坐标 (x, y, z)
    precision mediump float;
    attribute vec3 a_Position;
    attribute vec4 a_Color;
    varying vec4 v_Color;
    uniform mat4 u_Matrix;
    void main(){
      gl_Position =  u_Matrix * vec4(a_Position, 1);
      v_Color = a_Color;
    }

增加旋转动画效果：每隔 50 ms 分别绕 X 轴和 Y 轴转动 1 度，然后将旋转对应的矩阵传给顶点着色器。

//生成单位矩阵
var initMatrix = matrix.identify();
var currentMatrix = null;
var xAngle = 0;
var yAngle = 0;
var deg = Math.PI / 180;
function animate(e) {
      if (timer) {
        clearInterval(timer);
        timer = null;
      } else {
        timer = setInterval(() => {
          xAngle += 1;
          yAngle += 1;
          
          currentMatrix = matrix.rotationX(deg * xAngle);
          currentMatrix = matrix.rotateY(currentMatrix, deg * yAngle);
          gl.uniformMatrix4fv(u_Matrix, false, currentMatrix);
          render(gl);
        }, 50);
      }
    }

我们看下效果：

img

可以看到，渲染画面不再只是一幅静态的平面了，而是一个能够自由转动的立方体。

实现球体​

我们可以将球体按照纬度等分成 n 份，形成 n 个圆面，每个圆面的 Y 坐标都相同，然后将每个圆面按照经度划分成 m 份，形成 m 个顶点，这 m 个顶点的 Y 坐标也都相同。按照这个逻辑，我们思考下球体的顶点生成过程：

function createSphere(radius, divideByYAxis, divideByCircle) {
  let yUnitAngle = Math.PI / divideByYAxis;
  let circleUnitAngle = (Math.PI * 2) / divideByCircle;
  let positions = [];
  for (let i = 0; i <= divideByYAxis; i++) {
    let yValue = radius * Math.cos(yUnitAngle * i);
    let yCurrentRadius = radius * Math.sin(yUnitAngle * i);

    for (let j = 0; j <= divideByCircle; j++) {
      let xValue = yCurrentRadius * Math.cos(circleUnitAngle * j);
      let zValue = yCurrentRadius * Math.sin(circleUnitAngle * j);
      positions.push(xValue, yValue, zValue);
    }
  }

  let indices = [];
  let circleCount = divideByCircle + 1;
  for (let j = 0; j < divideByCircle; j++) {
    for (let i = 0; i < divideByYAxis; i++) {
      indices.push(i * circleCount + j);
      indices.push(i * circleCount + j + 1);
      indices.push((i + 1) * circleCount + j);

      indices.push((i + 1) * circleCount + j);
      indices.push(i * circleCount + j + 1);
      indices.push((i + 1) * circleCount + j + 1);
    }
  }
  return {
    positions: new Float32Array(positions),
    indices: new Uint16Array(indices)
  };
}

通过这个函数，我们得到了一个顶点对象，该对象包含所有顶点的坐标信息和索引信息。接下来我们为球体的每个三角面增加颜色信息。

我们知道，如果一个顶点的坐标相同，颜色不同的话，也必须视为两个顶点，否则会产生渐变颜色。因此，我们目前得到的球体的顶点仅仅坐标相同，如果我们要为每一个三角面绘制一种颜色的话，需要额外增加顶点，且不再使用索引绘制，而是采用顶点数组绘制。

function transformIndicesToUnIndices(vertex) {
  let indices = vertex.indices;
  let vertexsCount = indices.length;
  let destVertex = {};

  Object.keys(vertex).forEach(function(attribute) {
    if (attribute == 'indices') {
      return;
    }
    let src = vertex[attribute];
    let elementsPerVertex = getElementsCountPerVertex(attribute);
    let dest = [];
    let index = 0;
    for (let i = 0; i < indices.length; i++) {
      for (let j = 0; j < elementsPerVertex; j++) {
        dest[index] = src[indices[i] * elementsPerVertex + j];
        index++;
      }
    }
    let type = getArrayTypeByAttribName();
    destVertex[attribute] = new type(dest);
  });
  return destVertex;
}

该方法将我们第一步获取的球体顶点数组展开，得到所有三角形的顶点对象。

接着，我们可以为顶点施加颜色了。

function createColorForVertex(vertex) {
  let vertexNums = vertex.positions;
  let colors = [];
  let color = {
    r: 255,
    g: 0,
    b: 0
  };

  for (let i = 0; i < vertexNums.length; i++) {
    if (i % 36 == 0) {
      color = randomColor();
    }
    colors.push(color.r, color.g, color.b, 255);
  }

  vertex.colors = new Uint8Array(colors);
  return vertex;
}

生成球体顶点、增加三角面颜色这两个关键步骤做完之后，我们就可以执行绘制操作了，看下绘制后的效果：

img

实现椎体、柱体、台体​

椎体、柱体、台体可以归为一类构建方法，因为他们都受上表面、下表面、高度这三个因素的影响。 按照这种思路，我们再思考下它们的构建方法：

  • 定义上表面的半径：topRadius。
  • 定义下表面的半径：bottomRadius。
  • 定义高度：height。
  • 定义横截面的切分数量：bottomDivide。
  • 定义垂直方向的切分数量：verticalDivide。
 function createCone(
  topRadius,
  bottomRadius,
  height,
  bottomDivide,
  verticalDivide
) {
    
  let vertex = {};
  let positions = [];
  let indices = [];

  for (let i = -1; i <= verticalDivide + 1; i++) {
    let currentRadius = 0;
    if (i > verticalDivide) {
      currentRadius = topRadius;
    } else if (i < 0) {
      currentRadius = bottomRadius;
    } else {
      currentRadius =
        bottomRadius + (topRadius - bottomRadius) * (i / verticalDivide);
    }
    let yValue = (height * i) / verticalDivide - height / 2;
    if (i == -1 || i == verticalDivide + 1) {
      currentRadius = 0;
      if (i == -1) {
        yValue = -height / 2;
      } else {
        yValue = height / 2;
      }
    }

    for (let j = 0; j <= bottomDivide; j++) {
      let xValue = currentRadius * Math.sin((j * Math.PI * 2) / bottomDivide);
      var zValue = currentRadius * Math.cos((j * Math.PI * 2) / bottomDivide);
      positions.push(xValue, yValue, zValue);
    }
  }

  // indices
  let vertexCountPerRadius = bottomDivide + 1;
  for (let i = 0; i < verticalDivide + 2; i++) {
    for (let j = 0; j < bottomDivide; j++) {
      indices.push(i * vertexCountPerRadius + j);
      indices.push(i * vertexCountPerRadius + j + 1);
      indices.push((i + 1) * vertexCountPerRadius + j + 1);

      indices.push(
        vertexCountPerRadius * (i + 0) + j,
        vertexCountPerRadius * (i + 1) + j + 1,
        vertexCountPerRadius * (i + 1) + j
      );
    }
  }

  vertex.positions = new Float32Array(positions);
  vertex.indices = new Uint16Array(indices);
  return vertex;
}

当我们定义上表面的半径为 0 时，得出的形体是椎体：

let coneVertex = createCone(6, 0, 12, 12, 12);

效果如下：

img

当我们定义上表面和下表面的半径相同，且都不为 0 时，得出的形体是柱体：

let coneVertex = createCone(4, 4, 12, 12, 12);

效果如下：

img

当我们定义上表面和下表面的半径不同，且都不为 0 时，得出的形体是台体（也可以称为棱锥体）：

let coneVertex = createCone(6, 3, 12, 12, 12);

效果如下：

img

开发步骤总结​

绘制单个模型时， WebGL 的开发步骤：

  • 初始化阶段
    • 创建所有着色器程序。
    • 寻找全部 attribute 参数位置。
    • 寻找全部 uniforms 参数位置。
    • 创建缓冲区，并向缓冲区上传顶点数据。
    • 创建纹理，并上传纹理数据。
  • 首次渲染阶段
    • 为 uniforms 变量赋值。
    • 处理 attribute 变量
      • 使用 gl.bindBuffer 重新绑定模型的 attribute 变量。
      • 使用 gl.enableVertexAttribArray 启用 attribute 变量。
      • 使用 gl.vertexAttribPointer设置 attribute变量从缓冲区中读取数据的方式。
      • 使用 gl.bufferData 将数据传送到缓冲区中。
    • 使用 gl.drawArrays 执行绘制。
  • 后续渲染阶段
    • 对发生变化的 uniforms 变量重新赋值。
    • 每个模型的 attribute 变量。
      • 使用 gl.bindBuffer 重新绑定模型的 attribute 变量。
      • 使用 gl.bufferData 重新向缓冲区上传模型的 attribute 数据。
    • 使用 gl.drawArrays 执行绘制。

绘制多个物体​

创建模型类​

每个模型都有对应的顶点数据，包含顶点位置、颜色、法向量、纹理坐标等，我们将这些数据用一个顶点缓冲对象来表示，每个属性对应一个 attribute 变量。除了顶点数据，还需要有众多 uniforms 变量，uniforms 变量存储和顶点无关的属性，比如模型变换矩阵、模型视图投影矩阵MVP，（后续我们用 MVP 指代模型视图投影矩阵），法向量矩阵，光照等。既然模型有这么多共同的属性，那么我们把模型抽象出来。

定义一个模型类，模型类自身属性有模型矩阵u_ModelMatrix，MVP 矩阵u_Matrix，以及所有的 uniforms 变量，顶点缓冲数据。

//模型类
function Model(bufferInfo, uniforms ){
    this.uniforms = uniforms || {};
    this.u_Matrix = matrix.identity();
    this.bufferInfo = bufferInfo || {};
    
    // 偏移
    this.translation = [0, 0, 0];
    // 旋转角度
    this.rotation = [0, 0, 0];
    // 缩放
    this.scalation = [1, 1, 1];
}

matrix.identity 方法生成一个单位矩阵。

设置顶点对象​

提供一个为模型提供顶点数据的方法，顶点数据用一个对象表示，对象的属性用着色器中属性名称来 表示，对应顶点属性。一个完整的 bufferInfo 包含如下内容：

bufferInfo = {
    attributes:{
        a_Positions: {
            buffer: buffer,
            type: gl.FLOAT,
            normalize: false,
            numsPerElement: 4,
        },
        a_Colors:{
            buffer:buffer,
            type: gl.UNSIGNED_BYTE,
            normalize: true,
            numsPerElement: 4
        },
        a_Normals:{
            buffer:buffer,
            type: gl.FLOAT,
            normalize: false,
            numsPerElement: 3
        },
        a_Texcoords:{
            buffer:buffer,
            type: gl.FLOAT,
            normalize: false,
            numsPerElement: 2
        }
    },
    indices:[],
    elementsCount: 30
}

indices 代表顶点的索引数组， elementsCount 表示顶点的个数。buffer 代表 WebGL 创建的 buffer 对象，里面存储着对应的顶点数据。

顶点数据对象除了可以在初始化时为 model 设置以外，还需要为 model 提供一个单独设置方法：

Model.prototype.setBufferInfo = function(bufferInfo){
    this.bufferInfo = bufferInfo || {};
}

我们最初得到的顶点模型数据一般是这种格式的：

let vertexObject = {
    positions: [],
    normals: [],
    texcoords: [],
    indices: [],
    colors: []
}

这和我们上面设置的字段格式都不同，所以我们要添加一个适配器转换一下。

设置模型状态​

我们需要一些方法能够随时对模型对象的信息进行修改，比如位移，旋转角度，缩放比例等，最后还需要增加一个 preRender 预渲染方法，在绘制之前更新矩阵。

设置模型位移。​

位移的设置包含同时对三个分量设置以及对每个分量单独设置：

  • translate：对模型设置 X 轴、Y 轴、Z 轴方向的偏移。
  • translateX：对模型设置 X 轴偏移。
  • translateY：对模型设置 Y 轴偏移。
  • translateZ：对模型设置 Z 轴偏移。
Model.prototype.translate = function(tx, ty, tz){
    this.translateX(tx);
    this.translateY(ty);
    this.translateZ(tz);
}
Model.prototype.translateX = function(tx){
    this.translation[0] = tx || 0;
}
Model.prototype.translateY = function(ty){
    this.translation[1] = ty || 0;
}
Model.prototype.translateZ = function(tz){
    this.translation[2] = tz || 0;
}

设置模型缩放比例。​

缩放比例的设置包含同时对三个分量设置以及对每个分量单独设置：

  • scale：对模型设置 X 轴、Y 轴、Z 轴上的缩放比例。
  • scaleX：对模型设置 X 轴缩放比例。
  • scaleY：对模型设置 Y 轴缩放比例。
  • scaleZ：对模型设置 Z 轴缩放比例。
Model.prototype.scale = function(sx, sy, sz){
    this.scaleX(sx);
    this.scaleY(sy);
    this.scaleZ(sz);
}
Model.prototype.scaleX = function(sx){
    this.scalation[0] = sx || 1;
}
Model.prototype.scaleY = function(sy){
    this.scalation[1] = sy || 1;
}
Model.prototype.scaleZ = function(sz){
    this.scalation[2] = sz || 1;
}

设置模型旋转角度。​

模型旋转角度的设置包含同时对三个分量设置以及对每个分量单独设置：

  • rotate：对模型设置 X轴、Y轴、Z 轴上的旋转角度。
  • rotateX：对模型设置 X 轴旋转角度。
  • rotateY：对模型设置 Y 轴旋转角度。
  • rotateZ：对模型设置 Z 轴旋转角度。
Model.prototype.rotate = function(rx, ry, rz){
    this.rotateX(rx);
    this.rotateY(ry);
    this.rotateZ(rz);
}
Model.prototype.rotateX = function(rx){
    this.rotation[0] = rx || 0;
}
Model.prototype.rotateY = function(ry){
    this.rotation[1] = ry || 0;
}
Model.prototype.rotateZ = function(rz){
    this.rotation[2] = rz || 0;
}

预渲染。​

在将模型矩阵以及模型的 MVP 矩阵传递给 GPU 之前，我们对模型矩阵以及 MVP 矩阵重新计算。

  • rotate：对模型设置 X 轴、Y 轴、Z 轴上的旋转角度。
  • rotateX：对模型设置 X 轴旋转角度。
  • rotateY：对模型设置 Y 轴旋转角度。
  • rotateZ：对模型设置 Z 轴旋转角度。
Model.prototype.preRender =  function( viewMatrix, projectionMatrix){
    let modelMatrix = matrix.identity();
  if (this.translation) {
    modelMatrix = matrix.translate(
      modelMatrix,
      this.translation[0],
      this.translation[1],
      this.translation[2]
    );
  }
  if (this.rotation) {
    if (this.rotation[0] !== undefined)
      modelMatrix = matrix.rotateX(modelMatrix, degToRadians(this.rotation[0]));
    if (this.rotation[1] !== undefined)
      modelMatrix = matrix.rotateY(modelMatrix, degToRadians(this.rotation[1]));
    if (this.rotation[2] !== undefined)
      modelMatrix = matrix.rotateZ(modelMatrix, degToRadians(this.rotation[2]));
  }
  if (this.scalation) {
    modelMatrix = matrix.scale(
      modelMatrix,
      this.scalation[0],
      this.scalation[1],
      this.scalation[2]
    );
  }

  this.u_ModelMatrix = modelMatrix;

  //重新计算 MVP 矩阵

  this.u_Matrix = matrix.multiply(viewMatrix, this.u_ModelMatrix);
  this.u_Matrix = matrix.multiply(projectionMatrix, this.u_Matrix);
}

封装顶点数据的操作​

最为重要的是顶点数据，它们是模型的基本组成元素，顶点数据一般包含如下几个属性：

  • 颜色信息
  • 位置信息
  • 法向量信息
  • 索引信息
  • 纹理坐标
bufferInfo = {
    colors: [],
    positions: [],
    normals: [],
    indices: [],
    texcoords: []
}

我们有了这些顶点信息，还需要通过 attribute 变量传递给 GPU，所以，我们还需要找到对应的 attribute 变量。

在着色器中命名 attribute 变量时，我们通常使用 a_ 开头，后面跟着顶点属性名称，按照这种规范命名也方便我们在 JavaScript 中对变量进行赋值。

attribute vec4 a_Positions;
attribute vec3 a_Normals;
attribute vec2 a_Texcoords;
attribute vec4 a_Colors;

那么我们查找变量时，可以这样查找：

let attributesCount = gl.getProgramParameter(program, param);

当 pname 为 gl.ACTIVE_ATTRIBUTES时，返回program绑定的顶点着色器中 attribute 变量的数量 attributesCount。

有了变量数量，我们就可以对变量进行遍历了。

for(let i = 0; i< attributesCount; i++){
    let attributeInfo = gl.getActiveAttrib(program, i);
}

attributeInfo 对象包含 attribute 的变量名称 name，有了name我们就能够用 JavaScript 查找该 attribute 变量了：

let attributeIndex = gl.getAttribLocation(program, attributeInfo.name);

接着是熟悉的对变量的启用、读取缓冲区方式的设置了，我们将这些操作封装到一个方法中。

function createAttributeSetter(attributeIndex){
    return function(bufferInfo){
        gl.bindBuffer(gl.ARRAY_BUFFER, bufferInfo.buffer);
        gl.enableVertexAttribArray(attributeIndex);
        gl.vertexAttribPointer(
          attributeIndex,
          bufferInfo.numsPerElement || bufferInfo.size,
          bufferInfo.type || gl.FLOAT,
          bufferInfo.normalize || false,
          bufferInfo.stride || 0,
          bufferInfo.offset || 0
        );
    }
}

定义一个 attribute 变量设置对象，对每个 attribute 绑定上面实现的设置方法createAttributeSetter。

let attributeSetter = {};
for(let i = 0; i< attributesCount; i++){
    let attributeInfo = gl.getActiveAttrib(program, i);
    let attributeIndex = gl.getAttribLocation(program, attributeInfo.name);
    attributeSetter[attributeInfo.name] = createAttributeSetter(attributeIndex);
}
return attributeSetter;

以上是对着色器的各个attribute变量初始化操作，那么当我们需要对这些变量赋值时，就可以调用attribute 变量对应的 setter 函数对 attribute 进行设置了。

封装 uniforms 变量操作。​

那么，除了 attribute 变量，程序中还充斥着很多 uniforms 变量，uniforms 变量是与顶点无关的，即不管执行多少遍顶点操作， uniforms 变量始终保持不变。

像 attribute 变量一样，我们仍然需要先找到所有 uniforms 变量：

let uniformsCount = gl.getProgramParameter(program, gl.ACTIVE_UNIFORMS);

之后，遍历所有 uniforms 变量，根据 uniforms 变量名称，生成 uniforms 赋值函数。

let uniformsSetters = {};
for(let i = 0; i< uniformsCount; i++){
    let uniformInfo = gl.getActiveUniform(program, i);
      if (!uniformInfo) {
        break;
      }
      let name = uniformInfo.name;
      if (name.substr(-3) === '[0]') {
        name = name.substr(0, name.length - 3);
      }
      var setter = createUniformSetter(program, uniformInfo);
      uniformSetters[name] = setter;
}

uniforms 赋值函数比较繁琐一些，只因 uniforms 变量类型比较多，我们需要针对 uniforms 变量类型，编写对应的赋值函数。

let enums = {
        FLOAT_VEC2: {
            value: 0x8B50,
            setter: function(location, v){
                gl.uniform2fv(location, v);
            }
        },
        FLOAT_VEC3: {
            value: 0x8B51,
            setter: function(location, v){
                gl.uniform3fv(location, v);
            }
        }
        FLOAT_VEC4: {
            value: 0x8B52,
            setter: function(location, v){
                gl.uniform3fv(location, v);
            }
        },
        INT_VEC2: {
            value: 0x8B53,
            setter: function(location, v){
                gl.uniform2iv(location, v);
            }
        },
        INT_VEC3: {
            value: 0x8B54,
            setter: function(location, v){
                gl.uniform3iv(location, v);
            }
        },
        INT_VEC4: {
            value: 0x8B55,
            setter: function(location, v){
                gl.uniform4iv(location, v);
            }
        },
        BOOL: {
            value: 0x8B56,
            setter: function(location, v){
                gl.uniform1iv(location, v);
            }
        },
        BOOL_VEC2: {
            value: 0x8B57,
            setter: function(location, v){
                gl.uniform2iv(location, v);
            }
        },
        BOOL_VEC3: {
            value: 0x8B58,
            setter: function(location, v){
                gl.uniform3iv(location, v);
            }
        },
        BOOL_VEC4: {
            value: 0x8B59,
            setter: function(location, v){
                gl.uniform4iv(location, v);
            }
        },
        FLOAT_MAT2: {
            value: 0x8B5A,
            setter: function(location, v){
                gl.uniformMatrix2fv(location, false, v);
            }
        },
        FLOAT_MAT3: {
            value: 0x8B5B,
            setter: function(location, v){
                gl.uniformMatrix3fv(location, false, v);
            }
        },
        FLOAT_MAT4: {
            value: 0x8B5C,
            setter: function(location, v){
                gl.uniformMatrix4fv(location, false, v);
            }
        },
        SAMPLER_2D: {
            value: 0x8B5E,
            setter: function(location, texture){
            gl.uniform1i(location, 0);
            gl.activeTexture(gl.TEXTURE0);
            gl.bindTexture(gl.TEXTURE_2D, texture);
          }
        },
        SAMPLER_CUBE: {
            value: 0x8B60,
            setter: function(location, texture){
                gl.uniform1i(location, 0);
            gl.activeTexture(gl.TEXTURE0);
            gl.bindTexture(gl.TEXTURE_CUBE_MAP, texture);
            }
        },
        
        INT: {
            value: 0x1404,
            setter: function(location, v){
                gl.uniform1i(location, v);
            }
        },
        
        FLOAT: {
            value: 0x1406,
            setter: function(location, v){
                gl.uniform1f(location, v);
            }
        }
};

enums 是所有的变量类型，但没有包含普通数组，所以我们还需要通过 uniformInfo.size 属性判断该 uniform 变量是否是数组，uniform 变量的 size 大于 1 并且该变量名称的最后三个字符是[0]，说明该 uniform 变量是数组类型，大家可以尝试一下。

有两点需要大家注意： 1、如果 uniform 或者 attribute 变量只是在着色器中进行了定义，但没有被使用，那么它将被编译器抛弃，我们通过gl.getProgramParameter(program, gl.ACTIVE_UNIFORMS)这种方式获取不到该变量。 2、uniform 和 attribute 变量的数量并不是可以无限定义的，而是有一定上限，不同平台数量不同，一般 windows 平台 256 个，mac 和 linux 平台一般为 1024 个，如果定义数量超过这个上限，着色器程序会报编译错误。

function createUniformSetter(gl, program, uniformInfo) {
    let uniformLocation = gl.getUniformLocation(program, uniformInfo.name);
    let type = uniformInfo.type;
    let isArray = uniformInfo.size > 1 && uniformInfo.name.substr(-3) === '[0]';
    
    if(isArray && type == enums.INT.value){
        return function(v) {
          gl.uniform1iv(location, v);
        };
    }
    if(isArray && type == enums.FLOAT.value){
        return function(v) {
          gl.uniform1fv(location, v);
        };
    }
    return function createSetter(v){
        return enums[getKeyFromType(type)].setter(location, v)
    }
}

以上就是 uniforms 变量的初始化过程，相对繁琐，但比较简单，容易理解。

绘制多个物体​

既然有了模型类、uniforms 和 attribute 变量的赋值函数，接下来我们就可以创建一个模型列表和一个渲染列表，模型列表中存放所有模型对象，渲染列表中存放着待渲染的对象。

// 渲染列表
let renderList = new List();
// 模型列表
let modelList = new list();

// 列表类
function List(list){
    this.list = list || [];
    this.uuid = list.length;
}
// 添加对象
List.prototype.add = function(object){
    object.uuid = this.uuid;
    this.list.push(object);
    this.uuid++;
}
// 删除对象
List.prototype.remove = function(object){
    this.list.splice(object.uuid, 1);
}
// 查找对象
List.prototype.get = function(index){
    return this.list[index];
}
// 遍历列表
List.prototype.forEach = function(callback){
    return this.list.forEach(callback);
}

模型列表和渲染列表的区别在于，渲染列表只存储和渲染相关的数据，比如着色器程序，模型的顶点缓冲数据，uniforms 数据等。

一个完整的模型对象有如下内容：

let modelObject={
    // 偏移状态
    translation:[0, 0, 0],
    // 缩放状态
    scalation:[1, 1, 3],
    // 旋转状态
    rotation:[30, 60, 100],
    bufferInfo:{
        // 顶点属性
        attributes:{
            // 顶点坐标
            a_Position: {
                buffer: [],
                type: gl.FLOAT,
                normalize: false,
                numsPerElement: 4
            },
            ...
        },
        // 顶点索引
        indices: [],
        // 顶点数量
        elementsCount: 30
    },
    uniforms: {
        // MVP 矩阵
        u_Matrix: ...,
        // 模型矩阵
        u_ModelMatrix: ...,
        // 法向量矩阵
        u_NormalMatrix: ...,
        // 全局光照
        u_LightColor: ...,
        ...
    }
}

而一个渲染对象通常包含对应模型的几个属性：

let renderObject = {
    // 模型
    bufferInfo: modelObject.bufferInfo,
    program: program,
    uniforms: modelObject.uniforms,
}

添加一个新模型时，我们只需要初始化模型对象，添加到 objectList 中，同时往 renderList 中添加渲染对象。

let cube = createCube(5, 5, 5);
let cubeModel = new Model(cube);
objectList.add(cubeModel);
let renderObject= {
    program: program,
    model: cubeModel,
    primitive: 'TRIANGLES',
    renderType: 'drawArrays'
}
renderList.add(renderObject);

每次渲染时，首先遍历 objectList 中的模型对象，计算模型的 uniforms 变量，比如代表模型状态的 MVP 矩阵，模型矩阵，法向量矩阵等，以及顶点数据 bufferInfo，然后遍历 renderList 中的渲染对象，设置对应的 bufferInfo 和 uniforms 变量 ，执行绘制即可。

objectList.forEach(function(modelObject){
    // 计算相关 uniforms 属性。
    modelObject.preRender();
})
renderList.forEach(function(renderObject){
    let bufferInfo = renderObject.model.bufferInfo;
    let uniforms = renderObject.model.uniforms;
    let program = renderObject.program;
    // 往顶点缓冲区传递数据
    setBufferInfos(gl, program, bufferInfo);
    // 设置 uniforms 变量。
    setUniforms(gl, program, uniforms);
    // 绘制
    if (renderObject.renderType === 'drawElements') {
        if (bufferInfo.indices) {
            gl.drawElements(object.primitive, bufferInfo.indices.length, gl.UNSIGNED_SHORT, 0);
            return;
        } else {
            console.warn('model buffer does not support indices to draw');
            return;
        }
    } else {
          gl.drawArrays(gl[object.primitive], 0, bufferInfo.elementsCount);
    }
})

计算机表示光照​

颜色并不是客观存在的东西，只是一个视觉效果，决定这个视觉效果的关键因素是有三个：光、物体、视觉系统。

当光线照射到物体上时，物体能够吸收可见光的一部分，并反射不能吸收的那部分，反射出来的这部分可见光会刺激人眼，经过视神经传到大脑，形成对物体的色彩信息，这就是我们所说的颜色人眼看到的物体是什么颜色，就代表这个物体反射该颜色。

颜色在计算机中的表示​

在计算机中创建一个光源时，需要给光源设置一个颜色（光源也是有颜色的哦），我们给光源设置为白色：

以下的代码部分为 GLSL 语法。

vec3 light = vec3(1, 1, 1);

假设我们有一个物体是红色的：

vec3 color = vec3(1, 0, 0);

在计算机领域中，将光源颜色的各个分量与物体颜色的各个分量相乘，得到的就是物体所反射的颜色，即该物体在该光源照射下进入人眼的颜色：

vec3 resultColor = light * color

在 GLSL 语言中，vec3 与 vec3 相乘的实质是将两个 vec3 的分量分别相乘，得到一个新的 vec3。

得到的结果是 vec3(1 * 1, 1 * 0, 1 * 0) = vec3(1, 0, 0)，很明显，是红色，这也和现实生活中的表现一致。

前面讲了，如果蓝色的光线照射到红色的物体上，进入人眼的颜色是黑色，我们验证一下：

vec3 light = vec3(0, 0, 1);
vec3 color = vec3(1, 0, 0);
vec3 resultColor = light * color;

将光线的 rgb分量 和 物体颜色的 rgb 分量相乘：

resultColor = (0 * 1, 0 * 0, 1 * 0) = (0, 0, 0)

最终结果是黑色，很明显，和现实生活中的表现一致。

环境光​

在现实世界中，物体由于有本身材质的不同，对光线的反射效果也不同。材质粗糙的物体会将光线向各个方向进行反射，即漫反射，这也是现实生活中最为常见的反射类型，当漫反射的光线碰到另一个物体时，还会再次进行漫反射，所以，即使在没有光线照射到某个物体的情况下，其他物体的漫反射光也能照射到该物体，所以我们能够看到它。

那么在计算机中，如果想真实地模拟现实生活中没有光源直接照射物体时，通过其他物体的漫反射我们仍然能够看到该物体的情况，耗费的算力特别大，所以定义一种环境光的概念，来近似模拟这种效果。

环境光要模拟的并不是有光线照射下的漫反射，而是多个物体的漫反射互相作用的光线效果。

环境光计算​

假设有一个光源，发出的光线是白色光：

vec3 lightColor = vec3(1, 1, 1);

我们定义环境光的常量因子为 0.1

float ambientFactor = 0.1;

那么环境光的计算如下：

vec3 ambientColor = ambientFactor * lightColor;

GLSL中浮点数和 vec 向量相乘的实质是将该浮点数分别与vec向量的各个分量相乘，并返回新的 vec向量

计算出的环境光是： ambientColor = (1 * 0.1, 0.1 * 1, 0.1 * 1) = (0.1, 0.1, 0.1)

给物体增加环境光​

默认有一个白色的环境光在里面的

之前的片元着色器

gl_FragColor = v_Color;

其实可以理解为一个强度因子为 1 的白色光源：

vec3 ambientFactor = 1.0;
vec3 lightColor = vec3(1, 1, 1);
vec3 ambientColor = ambientFactor * lightColor;
gl_FragColor = vec4(ambientColor, 1) * v_Color;

那这次，我们要改变强度因子，同时改变光线颜色，所以我们要定义两个常量，强度因子u_AmbientFactor和光源颜色u_LightColor。

增加了环境光的片元着色器如下：

    precision mediump float;
    varying vec4 v_Color;
    //光源颜色
    uniform vec3 u_LightColor;
    //环境光强度因子
    uniform float u_AmbientFactor;
    void main(){
      vec3 ambientColor = u_AmbientFactor * u_LightColor;
      gl_FragColor = vec4(ambientColor, 1) * v_Color;
    }

接下来我们需要通过 JavaScript 给片元着色器传递这两个常量：

var u_AmbientFactor = gl.getUniformLocation(program, 'u_AmbientFactor');
var u_LightColor = gl.getUniformLocation(program, 'u_LightColor');

找到这两个常量位置，我们需要为他们传递强度因子和光线颜色，强度因子默认值是 0.2，光线颜色默认是白色：

<div>
    环境光因子：
    <input id="ambientFactor" class="range" type="range" min="0" max="1" step="0.01" value="0.2" /> 
</div>
<div>
    光线颜色：
    <input id="lightColor" class="color" type="color" value="#FFFFFF" />
</div>

冯氏光照模型(漫反射)​

现实世界中一个物体展示出来的颜色除了受环境光的影响，还要看该物体是否被光源直接照射，以及物体本身的材质

除了物体本身的因素会对最终进入人眼的颜色产生影响，人眼、物体、光源之间的位置也会决定进入人眼的颜色。

现实生活中的光照效果如此复杂，而且受到很多因素的影响，即使在计算机硬件飞速发展的今天，也依然会消耗很大的算力，无法精确模拟这种效果，所以需要一种能够近似现实光照效果的简化模型。业界比较著名的是冯氏光照模型（Phong Lighting Model）。

冯氏光照模型模拟现实生活中的三种情况，分别是环境光(Ambient)、漫反射(Diffuse)和镜面高光(Specular)。

  • 环境光：环境光在上节已经讲过了，主要用来模拟晚上或者阴天时，在没有光源直接照射的情况下，我们仍然能够看到物体，只是偏暗一些，通常情况我们使用一个较小的光线因子乘以光源颜色来模拟。
  • 漫反射：漫反射是为了模拟平行光源对物体的方向性影响，我们都知道，如果光源正对着物体，那么物体正对着光源的部分会更明亮，反之，背对光源的部分会暗一些。在冯氏光照模型中，漫反射分量占主要比重。
  • 镜面高光：为了模拟光线照射在比较光滑的物体时，物体正对光源的部分会产生高亮效果。该分量颜色会和光源颜色更接近。

有了冯氏光照模型，我们就可以通过这三个分量模拟出相对真实的光照效果了

计算漫反射光照​

当一束光线照射到物体表面时，光线的入射角越小，该表面的亮度就越大，看上去也就越亮。反之，该表面的亮度就越小，看上去越暗。

img

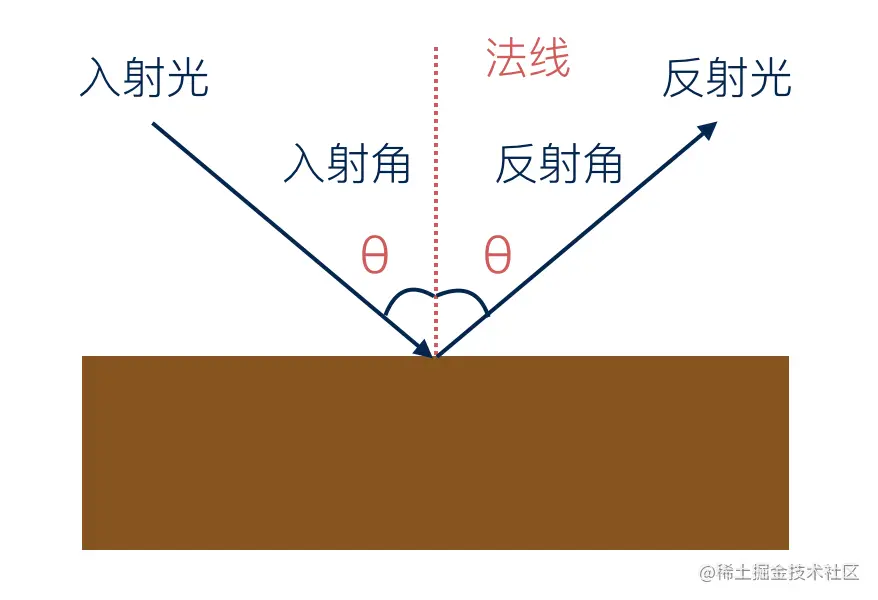
这种现象我们该如何在计算机中表示呢？

关键在于入射角的表示与光线强度的计算

入射角的表示与计算​

我们需要定义一个类似法线的概念，即法向量，法向量垂直于物体表面，并且朝向平面外部，如下图：

有了法向量，我们还需要光线照射方向，光线照射方向根据光源的不同有两种表示方法：

  • 平行光线
    • 光线方向是全局一致的，与照射点的位置无关，不会随着照射点的不同而不同，不是很真实。
  • 点光源。
    • 向四周发射光线，光线方向与照射点的位置有关，越靠近光源的部分越亮，光照效果比较真实。

计算反射光强度​

因为入射角的大小与反射光的亮度成反比，所以我们使用入射角的余弦值来表示漫反射的光线强度。

法向量​

法向量是垂直于顶点所在平面，指向平面外部的向量，只有方向，没有大小，类比光学现象中的法线，如下所示：

img

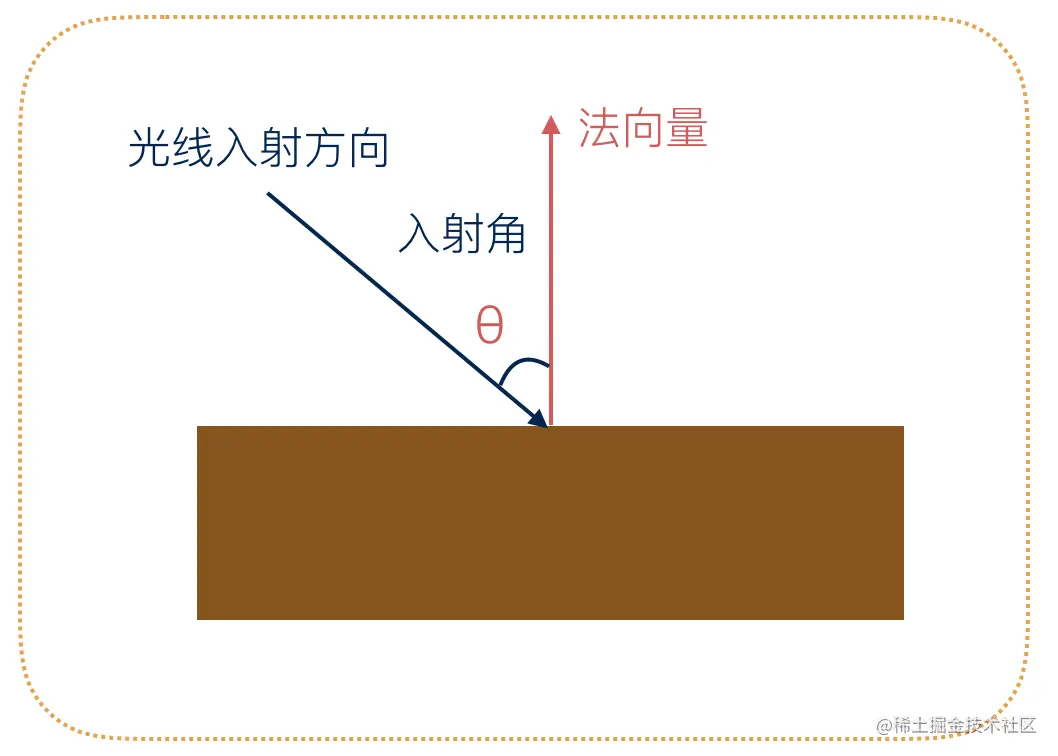
法向量存储在顶点属性中，为了便于计算入射角的余弦值，法向量的长度通常设置为 1。

除了法向量，我们还需要知道光线的入射角，即光源的照射方向向量和法向量的夹角

光源照射方向向量的计算​

光源位置坐标是基于世界坐标系的，所以我们在计算光源入射方向向量的时候，需要将照射点的坐标也转换到世界坐标系中。

在世界坐标系中，假设有一光源 p0 (x0, y0, z0)。

vec3 p0 = vec3(10, 10, 10);

光线照射到物体表面上的一点 p1 (x1, y1, z1)。

vec3 p1 = vec3(20, 25, 30);

那么光线照射在该点的方向向量为：

vec3 light_Direction = p1 - p0

GLSL中的 +、-、*、/ 操作符的左右两个数如果是向量的话，得出的新向量的各个分量等于原有向量逐分量的相减结果。

这样我们就得出了光源的照射方向向量。

计算漫反射光照​

有了入射角，我们的漫反射光照分量就可以求出来了。

  • 漫反射光照 = 光源颜色 * 漫反射光照强度因子
  • 漫反射光照强度因子 = 入射角的余弦值

通常我们如果要求入射角的余弦值，需要首先知道入射角，然后再求入射角的余弦值。不过由于我们使用的是向量，根据向量的运算规则，我们可以使用向量之间的点积，再除以向量的长度之积，就可以得出余弦值。

我们首先将两个向量归一化，转换成单位向量，然后进行点积计算求出夹角余弦。

归一化向量的实质是将向量的长度转换成 1，得出的一个单位向量。

所以我们需要两个数学方法来操作他们

  • dot
    • 求出两个向量的点积。
  • normalize
    • 将向量转化为长度为 1 的向量。

所幸的是，GLSL 内置了这两个函数方便我们计算，一些有名的 3D 框架中也包含这两个方法。

所以，我们的入射角余弦值就可以这样求出了：

//light_Direction表示光源照射方向向量。
//normal 代表当前入射点的法向量
vec3 light_Color = vec3(1, 1, 1);
float diffuseFactor = dot(normalize(light_Direction), normalize(normal))
vec4 lightColor = vec4(light_Color * diffuseFactor, 1);

这样我们就求出了漫反射光照的分量

平行光漫反射​

顶点着色器​

顶点着色器需要接收顶点法向量，插值化后传递给片元着色器，所以我们需要定义一个varying类型的 3 维向量来表示法向量，完整的顶点着色器如下：

// 顶点坐标
attribute vec4 a_Position;
// 顶点颜色
attribute vec4 a_Color;
// 顶点法向量
attribute vec3 a_Normal;
// 传递给片元着色器的法向量
varying vec3 v_Normal;
// 传递给片元着色器的颜色
varying vec4 v_Color;
// 模型视图投影变换矩阵。
uniform mat4 u_Matrix;

void main(){
    // 将顶点坐标转化成裁剪坐标系下的坐标。
    gl_Position = u_Matrix * vec4(a_Position, 1);
    // 将顶点颜色传递给片元着色器
    v_Color = a_Color;
    // 将顶点法向量传递给片元着色器
    v_Normal = a_Normal;
}

细心的读者已经看到了，着色器中我们使用了 GLSL 中的矩阵容器类型 mat4，4 * 4 矩阵，用来表示模型视图投影变换。我们将 4 阶矩阵左乘 4 维向量，即可表示对 4 维向量所表示的点执行 4 阶矩阵所表示的变换。

片元着色器​

漫反射光照分量在片元着色器中计算，按照上面的计算公式，我们需要接收顶点着色器传递过来的插值后的法向量v_Normal和全局光源位置 u_LightPosition，以及光线的颜色u_LightColor。

// 片元法向量
varying vec3 v_Normal;
// 片元颜色
varying vec4 v_Color;
// 光线颜色
uniform vec3 u_LightColor;
// 光源位置
uniform vec3 u_LightPosition;
void main(){
      // 环境光分量
      vec3 ambient = u_AmbientFactor * u_LightColor; 
      // 光源照射方向向量
      vec3 lightDirection = u_LightPosition - vec3(0, 0, 0);
      // 漫反射因子
      float diffuseFactor = dot(normalize(lightDirection), normalize(v_Normal));
      // 如果是负数，说明光线与法向量夹角大于 90 度，此时照不到平面上，所以没有光照，即黑色。
      diffuseFactor = max(diffuseFactor, 0.0);
      // 漫反射光照 = 光源颜色 * 漫反射因子。
      vec3 diffuseLightColor = u_LightColor * diffuseFactor;
      // 物体在光照下的颜色 = （环境光照 + 漫反射光照） * 物体颜色。
      gl_FragColor = v_Color * vec4((ambient + diffuseLightColor),1);   
}

JavaScript部分​

着色器的程序完成了，接下来我们需要给着色器传递数据了。和之前的例子相比，我们多了两个全局变量光照颜色、光照位置，以及一个顶点属性法向量。

首先我们给顶点增加法向量：

var normalInput = [    [0, 0, 1],  //前平面
    [0, 0, -1], //后平面
    [-1, 0, 0], //左平面
    [1, 0, 0], //右平面
    [0, 1, 0], //上平面
    [0, -1, 0] //下平面
];

各个平面的法向量准备好后，我们就可以为组成平面的顶点设置法向量属性了，限于篇幅，此处不再展示源码，大家可以在此处查看完整源代码 光照演示源码。

接下来，创建立方体的顶点数据：

var cube = createCube(10, 10, 10);

此处创建一个长、宽、高各位 10 的立方体，坐标原点在立方体中心。

接下来，我们设置光源位置，我们希望将光源放在立方体前面 z 轴坐标正方向 10 的位置。

gl.uniform3f(u_LightPosition, 0, 0, 10);

设置光源颜色为白色：

gl.uniform3f(u_LightColor, 1, 1, 1);

按照这种放置，光源在立方体的正前方，它始终照亮前面。我们看下演示效果：

img

JavaScript部分​

JavaScript 部分需要为顶点着色器传入模型矩阵u_ModelMatrix的值，那么，模型矩阵如何计算呢？还好矩阵库为我们解决了这个问题。

var modelMatirx = matrix.identity();
modelMatrix = matrix.rotateX(modelMatrix, Math.PI / 180 * (uniforms['xRotation']));

这里利用了矩阵库的两个方法identity 和 rotateX：

  • identity 用来初始化一个 4 维矩阵，对角线分量均为1。
  • rotateX 将原来的矩阵沿着 X 轴旋转，得到一个新的矩阵。

img

立方体正对光源的平面都能够被照亮了

点光源的漫反射​

前面的平行光漫反射可以模拟遥远的光源，比如太阳光，由于太阳距离地球过于遥远，所以光线照射在物体各个点的方向还是可以近似平行的。

但现实生活中还有很多人造光源，这些光源距离物体比较近，照在物体不同点时，入射角也会不一样，所以光照强度也有差别，在一个平面上产生距离光源近的部分比较亮，距离光源远的部分比较暗的效果。

接下来我们模拟这种情况。

我们在之前平行光漫反射的基础上进行改造，大家可以看到，之前的平行光漫反射计算入射角余弦时，是根据光源位置和世界坐标系的原点计算的入射角，只要我们不改变光源位置，那么光线方向就始终一致。

但是，点光源需要根据光源位置和入射点位置计算入射角，所以我们需要计算出入射点的世界坐标系坐标。

入射点的世界坐标系坐标的求法也比较简单，只需要左乘模型矩阵就可以了

顶点着色器​

顶点着色器需要定义一个入射点位置，插值化后传给片元着色器计算入射角的余弦。

...略
varying vec3 v_Position;
void main(){
    ...略
    v_Position = vec3(u_ModelMatrix * vec4(a_Position, 1));
}
片元着色器​

片元着色器部分的改变只有在计算光源入射方向时，用光源位置减去入射点位置：

...略
// 光源照射方向向量
vec3 lightDirection = u_LightPosition - v_Position;
...略

JavaScript部分不需要改动，我们看下演示效果：

img

可以看到，在点光源的作用下，平面上的不同点也产生了明暗效果。

物体缩放时的表现​

结束了吗？当然没有，我们还有一个问题没有解决。

假设有一物体表面被光线照射：

img

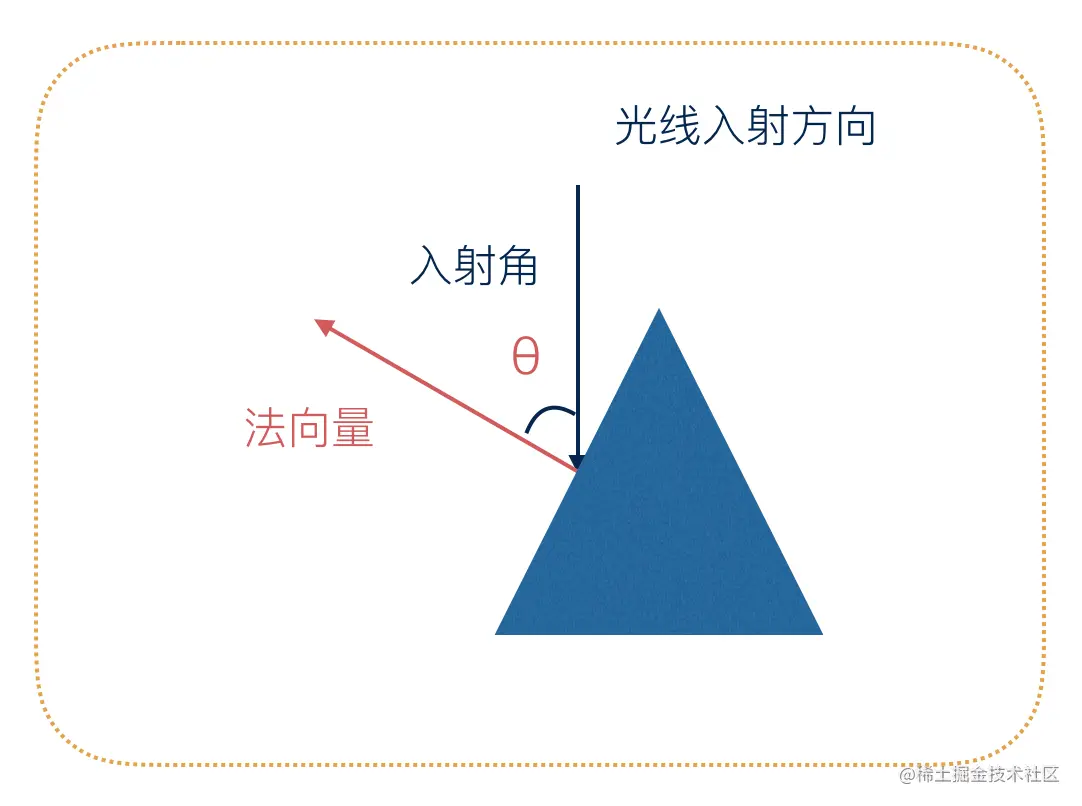
当对物体执行非等比缩放时，顶点法向量也会执行非等比缩放，但是执行缩放后的法向量却不再垂直于顶点所在平面了，如下图：

img

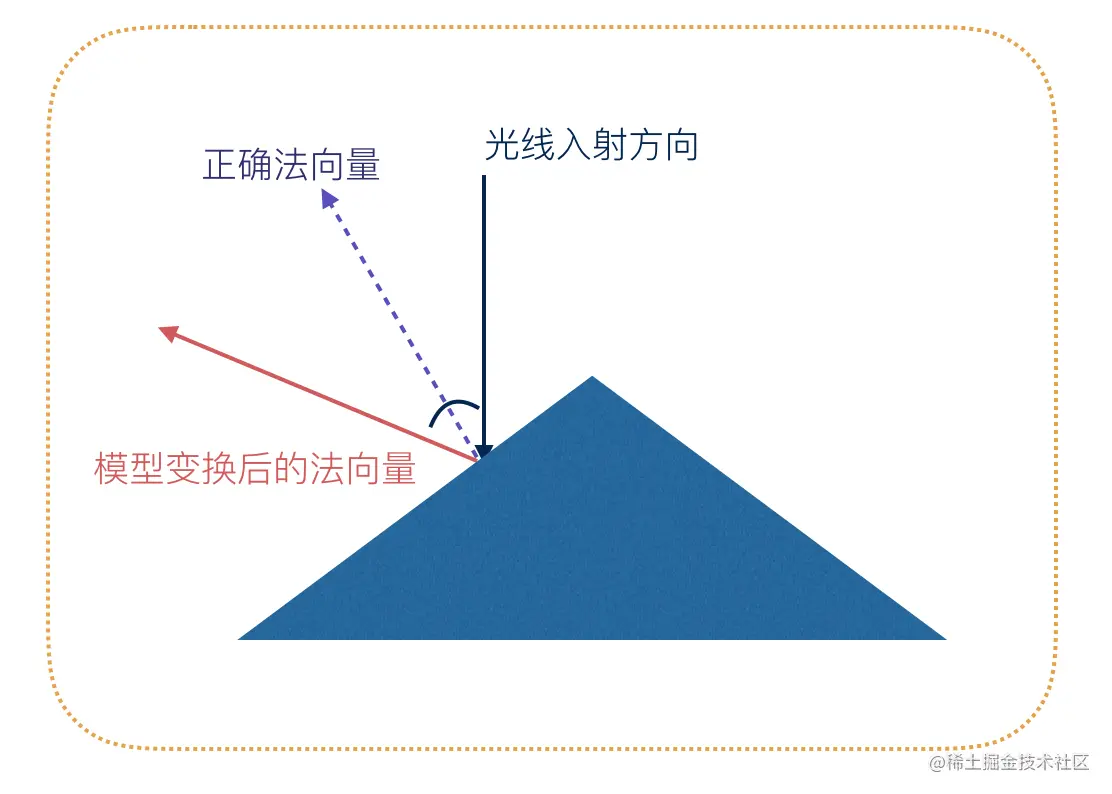
法向量不正确带来的后果是光照计算不准，表现如下：

img

可以看到，当我们队球体执行纵向放大的时候，放大的部分虽然正对着光源，但是没有光照。

因此，我们不能使用简单的模型矩阵来变换顶点法向量了。为了解决这个问题，我们需要专门为法向量的变换定义一个单独的矩阵法线矩阵，法线矩阵可以用「模型矩阵左上角的3维矩阵的逆矩阵的转置矩阵」来代替。听起来比较复杂，其实很简单。

  • 1、对模型矩阵执行逆矩阵操作。
  • 2、对上一步得出的矩阵执行转置矩阵。
  • 3、取上一步得出的矩阵的前三阶矩阵。

我们修改一下程序，顶点着色器和片元着色器部分不用改变，我们需要修改 JavaScript 部分。

我们使用矩阵库的两个方法 transpose 和 inverse 来对模型矩阵执行转置操作和求逆操作。

var normalMatrix = matrix.transpose(matrix.inverse(modelMatrix));

然后将该矩阵传递给顶点着色器即可，我们看下修改后的效果：

img

冯氏光照模型(增加镜面高光效果)​

镜面高光的表示与计算​

与漫反射分量相同，镜面高光也是根据光线的入射方向向量和法向量来决定的，只不过镜面高光还需要依赖视线的观察方向，也就是眼睛是从什么方向观察的物体。

视线方向向量与反射光向量的之间的夹角越小，夹角余弦值就会越大，那么人眼感受到的光照就会越强，反之，光照越暗。因此，我们使用夹角的余弦值表示镜面高光因子，然后再用镜面高光因子乘以光线颜色即可求出镜面高光分量：

img

  • 1、首先需要求出反射光向量reflectDirection和人眼视线方向向量viewDirection。
  • 2、归一化两个向量。
  • 3、求出两个归一化向量的点积，得到镜面高光因子。
  • 4、将上一步求出的高光因子乘以光线颜色，得到镜面高光分量。

本节我们使用 GLSL 内置的反射向量算法reflect(inVec, normal)，其中 inVec 为入射向量，方向由光源指向入射点，normal 为入射点的法向量。

计算反射光向量​

反射光向量在片元着色器中实现，参照上一节漫反射分量的计算，我们已经有了光源位置u_LightPosition和入射点位置v_Position，所以可以求得入射光向量：

//求出入射光向量
vec3 lightDirection = v_Position - u_LightPosition

切记，在使用GLSL 的reflect 函数计算反射光向量时，一定要确保入射光向量的方向是从光源位置指向入射点位置。

有了入射光向量，我们还需要入射点的法向量v_Normal，这个值已经从顶点着色器中插值化后传到片元着色器了，所以我们可以直接拿来用：

vec3 reflectDirection =reflect(normalize(lightDirection), normalize(v_Normal));

这样就求出了反射光向量，接下来我们计算视线观察向量。

计算视线观察向量​

我们将入射点到观察者的方向向量定义为视线观察向量，为了计算这个向量，我们需要知道入射点的位置以及观察者的位置，入射点的位置我们有了，现在需要观察者的位置，我们将人眼在世界坐标系下的坐标作为观察者位置，然后将其用 uniform 变量的形式传递到片元着色器中。

因此我们的片元着色器要增加一个 uniform 变量接收观察者坐标。

// 观察者坐标。
uniform vec3 viewPosition;

有了观察者坐标，我们就可以计算出视线观察向量了。

// 视线观察向量
vec3 viewDirection = viewPosition - v_Position;

计算镜面高光因子​

前面求出了视线观察向量和反射光向量，接下来我们就可以计算镜面高光因子了。

首先，归一化视线观察向量和反射光向量

viewDirection = normalize(viewDirection);
reflectDirection = normalize(reflectDirection);

然后计算这两个向量的点积，这里要注意一点，就是如果这两个向量的点积为负数，则说明视线观察向量和反射光向量大于 90 度，是没有反射光进入眼睛的，所以我们使用 max函数取点积和 0 之间的最大值。

// 镜面高光因子
float specialFactor = dot(viewDirection, reflectDirection);
// 如果为负值，一律设置为 0。
specialFactor = max(specialFactor, 0.0);

完整的片元着色器程序如下：

    precision mediump float;
    varying vec4 v_Color;
    uniform vec3 u_LightColor;
    uniform float u_AmbientFactor;
    uniform vec3 u_LightPosition;
    varying vec3 v_Position;
    varying vec3 v_Normal;
    uniform vec3 u_ViewPosition;
    void main(){
      // 环境光分量
      vec3 ambient = u_AmbientFactor * u_LightColor; //环境光分量
      // 光线照射向量
      vec3 lightDirection =  v_Position - u_LightPosition;
      // 归一化光线照射向量
      lightDirection= normalize(lightDirection);
      // 漫反射因子
      float diffuseFactor = dot(normalize(lightDirection), normalize(v_Normal));
      // 如果大于 90 度，则无光线进入人眼，漫反射因子设置为0。
      diffuseFactor = max(diffuseFactor, 0.0);
      // 漫反射光照
      vec3 diffuseLightColor =u_LightColor * diffuseFactor;
      
      // 归一化视线观察向量
      vec3 viewDirection = normalize(v_Position - u_ViewPosition);
        //反射向量
      vec3 reflectDirection = reflect(-lightDirection, normalize(v_Normal));
      
      // 初始化镜面光照因子
      float specialFactor = 0.0;
      // 如果有光线进入人眼。
      if(diffuseFactor > 0.0){
        specialFactor = dot(normalize(viewDirection), normalize(reflectDirection));
        specialFactor = max(specialFactor,0.0);
     }
     // 计算镜面光照分量
      vec3 specialLightColor  = u_LightColor * specialFactor * 0.5;
      // 计算总光照
      vec3 outColor = ambient + diffuseLightColor + specialLightColor;
      // 将物体自身颜色乘以总光照，即人眼看到的物体颜色。
      gl_FragColor = v_Color * vec4(outColor, 1); 
    }

加入光照之后，我们的着色器代码就变多了，但其实并不复杂，仅仅是取值、计算、赋值操作而已。

JavaScript 部分​

镜面光照我们需要为着色器传递一个人眼观察位置，所以我们的JavaScript 部分需要修改：

// 获取着色器全局变量 `u_ViewPosition`
var u_ViewPosition = gl.getUniformLocation(program, 'u_ViewPosition');

将人眼观察位置放置在 z 轴正方向 10 位置，即物体的前面。

var uniforms = {
    eyeX: 0,
    eyeY: 0,
    eyeZ: 10
};

gl.uniform3f(u_ViewPosition, uniforms['eyeX'], uniforms['eyeY'], uniforms['eyeZ']);

完整的代码大家可以参见这里，我们比较下加入镜面高光前后的效果。

无镜面高光时：

img

添加镜面高光后：

img

观察上面两幅图，我们能很直观地看到添加镜面高光后，球体正中央有一个明晃晃的光圈，符合真实世界中的场景。

反光度​

这个刺眼的光圈面积太大了，我们需要给它添加一个称为反光度(shininess)的参数约束光圈的大小，一个物体的反光度越大，反光率就越强，散射的光就越少，我们看到的高光面积就越小。

我们定义一个u_Shininess的变量表示物体的反光度，然后用前面求得的高光因子乘以 2 的shininess次幂作为最终的高光因子。这样就可以让我们的光圈变得小一些。

求幂计算可以通过GLSL 内置的公式 pow(2, shininess)求得。

specialFactor = max(specialFactor, 0.0);
specialFactor = pow(specialFactor, u_Shininess);

一般情况下，我们设置物体的反光度为 32 就可以了，但是特殊场景下，效果可能不理想，这时候，我们就需要根据实际情况调整反光度了。

我们将反光度设置成 32，看下增加反光度后的效果：

img

Blinn-Phong光照模型​

冯氏光照模型不仅能够很好的近似真实光照，而且性能也相当高。但是 这种光照在某些场景下仍然有些缺陷，大家观察前面没有添加反光度时的图片，应该能发现高光光圈边缘有一圈很明显的暗灰色断痕，但大家再看一下增加反光度后的效果，却没发现这种现象。这是为什么呢？

产生这个问题的原因是，在高光边缘部位，由于人眼视线向量和反射光向量夹角大于90度，那么夹角的余弦值便小于 0，按照冯氏光照模型的镜面光照算法，夹角余弦值小于 0 时， 我们的镜面高光分子系数就会用 0 来代替。所以高光边缘部位及以外的部分就没有了镜面光照分量，试想一下，如果反光度越小，镜面高光区域就越大，那高光区域边缘部位漫反射光的分量所占比重就会比较小，在高光边缘部位就会产生一种较大的亮度差，给人一种暗灰色断痕的感觉。反之，反光度越小，光圈越小，相应地，光圈周围漫反射光的分量所占比重就比较大，所以不会在高光边缘产生过大的亮度差。

如下图，反射光线和视线观察向量之间的夹角γ 大于90度，所以此时镜面高光分量为 0。

img

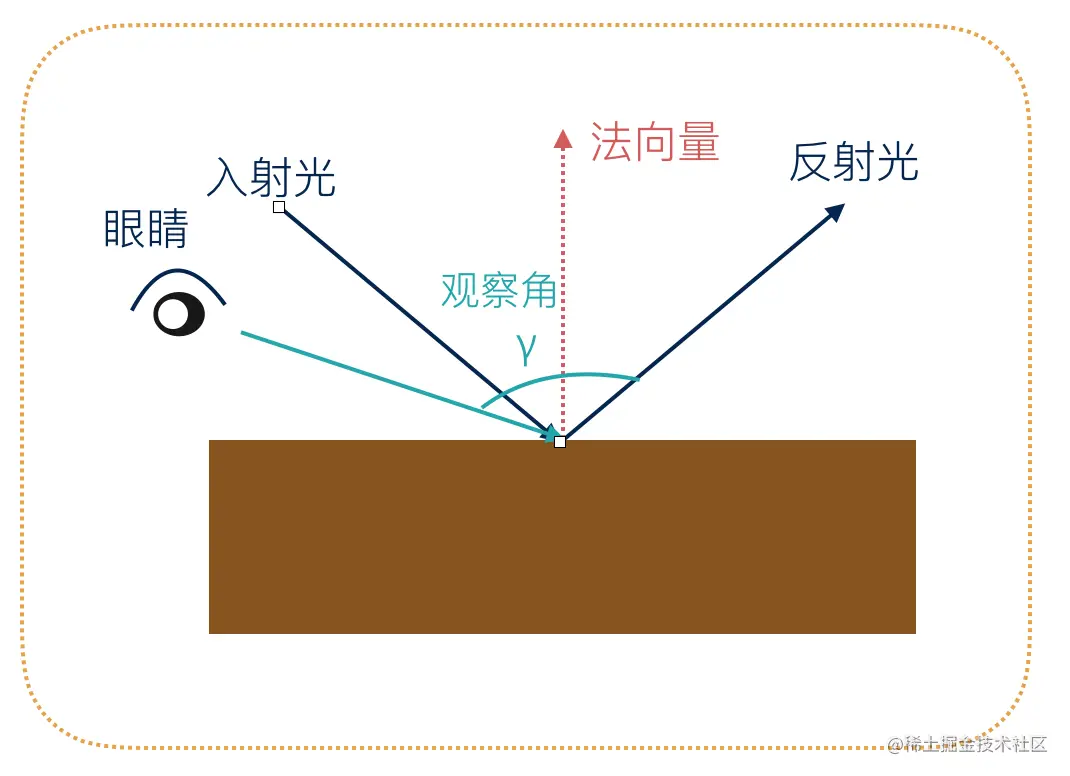
其实，这种观察角度，镜面高光分量还是应该有的，只是值比较小而已。所以，出现了 Blin Phong 光照模型，这种光照模型不再利用反射向量，而是采用了半程向量 ，半程向量是视线和反射光之间夹角的一半方向上的单位向量，利用半程向量和法向量之间的夹角余弦来表示镜面高光因子，半程向量和法向量之间的夹角越小，镜面高光分量越大，如下图所示：

img

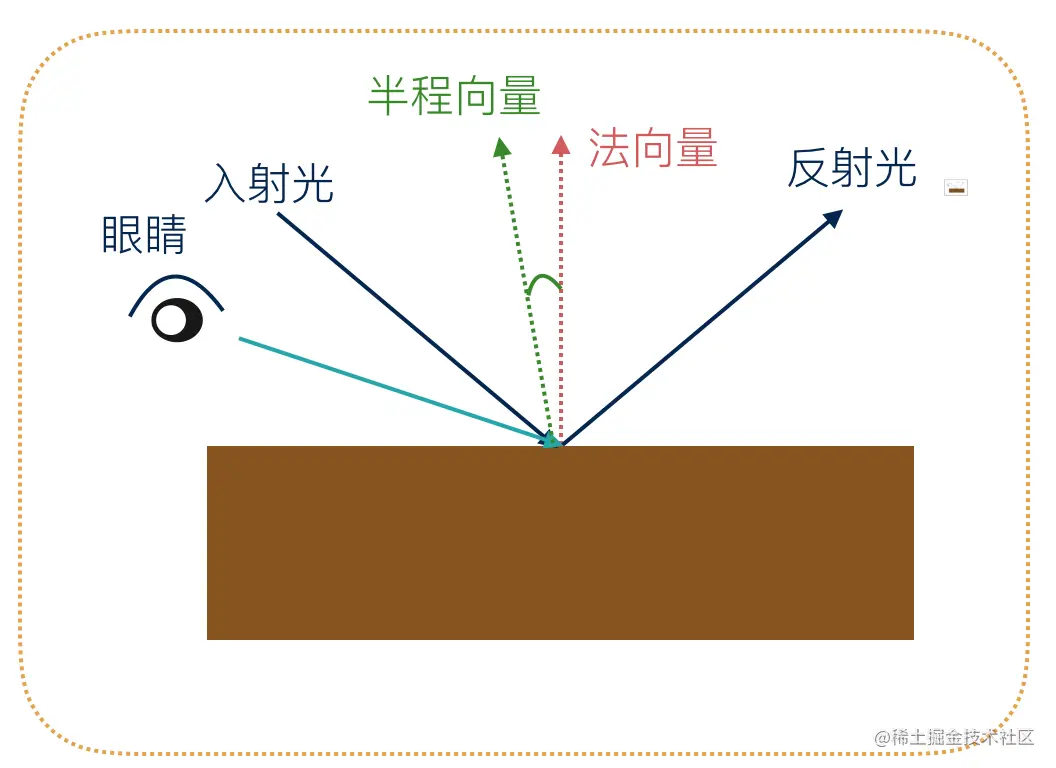
实现 Blin Phong 光照​

我们在冯氏光照代码的基础上加以修改，实现 Blin 光照模型。与冯氏光照模型不同的是，我们需要半程向量，半程向量该如何求呢？

按照向量的计算规则，半程向量只需要我们将视线观察向量和反射向量相加，然后将得出的结果归一化就可以求出了。

// 计算半程向量
vec3 halfVector = normalize(reflectDirection + viewDirection);
// 计算高光因子
float specialFactor = dot(normalize(v_Nomral), halfVector);

利用 GLSL 的内置函数，我们就很容易的求出来了。

从冯氏光照模型进化成 Blin光照模型，我们只需要改动这么一处就可以了，是不是觉得很简单呢？

好了，我们比较一下反光度同时为 1 的时候，冯氏光照和 Blin 光照之间的差别。

冯氏光照效果：

img

Blin 光照效果：

img

可以看到，采用 Blin光照模型后， 镜面高光区域过度的更加自然。

数学问题​

矩阵在 GLSL 中的存储特点​

WebGL 应用中的数据一般是从 CPU 传入 GPU 的，语言层面从 JavaScript 传入 GLSL。假如我们要把在 JavaScript 中生成的矩阵传入到 GLSL 中，那么就得保证生成的矩阵能够被 GLSL 所理解，换句话说，JavaScript 矩阵和 GPU 中的矩阵要有相同的表示形式，避免不必要的转换过程。

行主序和列主序​

存储顺序说明了线性代数中的矩阵如何在线性的内存数组中存储，按照存储方式分为行主序和列主序。

行主序是按照行向量的方式组织矩阵。列主序是按照列向量的方式组织矩阵

假设有一个 3 阶方阵 M：

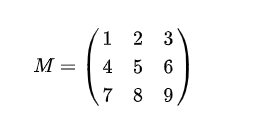
image-20220727152726273

那么它在内存中的排布方式如下：

img

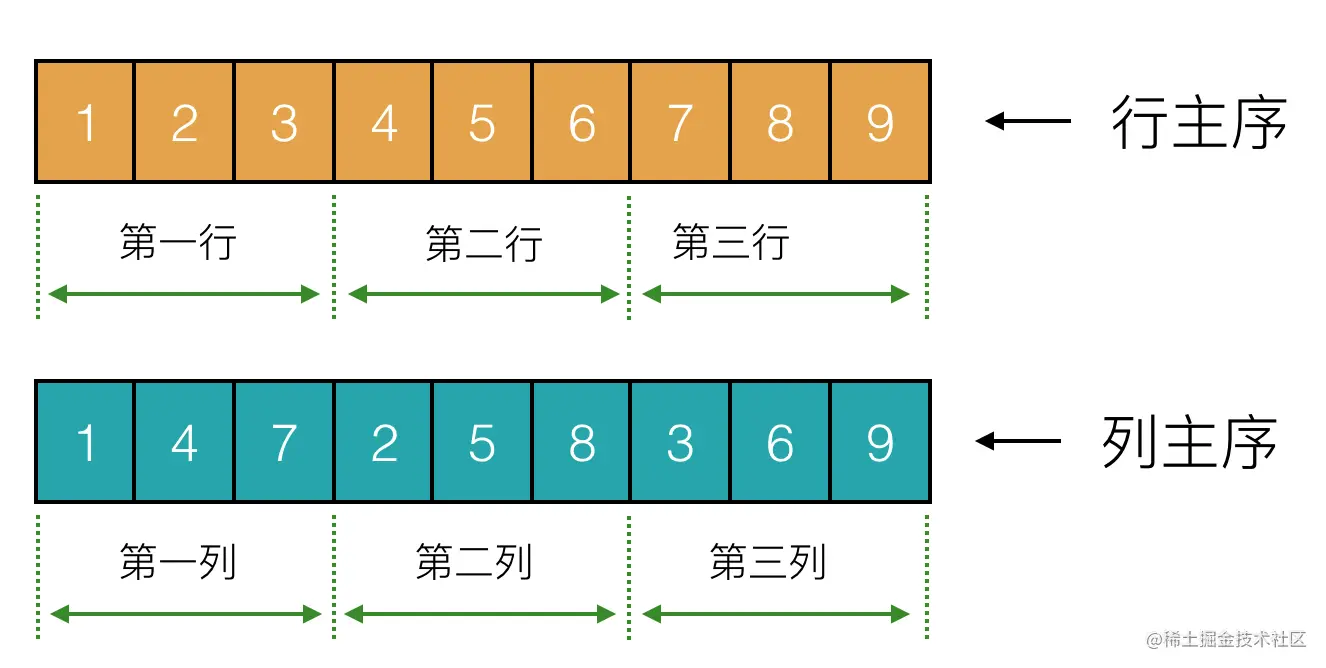
观察上面的图，就能够一目了然地看出行主序和列主序的区别了。

请务必谨记，D3D 中矩阵采用的是行主序的存储方式，GLSL 中采用的是列主序

JavaScript存储矩阵​

我们用数组来表示矩阵，但由于 JavaScript 数组是弱类型的，并没有严格按照内存位置进行排布，而 GLSL 中的矩阵元素是严格按照内存地址顺序排列的，所以我们需要将弱类型数组转化成二进制形式，通常我们使用 Float32Array 把弱类型数组转化成强类型数组。

let M = [1, 2, 3, 4, 5, 6, 7, 8, 9];
M = new Float32Array(M);

WebGL 坐标系​

WebGL 是如何把 3D 世界中的模型（物体）渲染到屏幕上的呢？ 这其中的最大难点就是坐标系的变换

顶点如何渲染到屏幕上​

如果想在屏幕上绘制一个点，我们需要将点的坐标从 CPU 通过 JavaScript 传递给 GPU ，GPU 接收到顶点坐标，进行一些坐标转换（通常将转换过程放在 JavaScript 中），然后将坐标赋值给 gl_Position：

gl_Position = vec4(x, y, z, 1);

请注意：gl_Position 接收一个 4 维向量表示的坐标，即(X, Y ,Z ,W)，W 不等于 0，这个坐标是在裁剪坐标系中，我们称它为裁剪坐标。

透视除法​

GPU 得到裁剪坐标后，下一步会对坐标进行透视除法。所谓透视除法就是将裁剪坐标的各个分量同时除以 W 分量，使得 W 分量为 1。经过透视除法得到的坐标便处在 NDC 坐标系（设备独立坐标系）中， NDC 坐标系是一个边长为 2 的正方体，超出正方体的顶点都将被抛弃，不会显示到屏幕上。

在 NDC 坐标系内的坐标都会落在【-1，1】之间，因此很多顶点坐标往往都是小数。

视口转换​

接下来，GPU 就要将顶点绘制到屏幕上了，顶点此时的坐标已经转变到 NDC 坐标系中，但是 NDC 坐标系和屏幕坐标系不一致，所以就产生了最后一个坐标变换，视口转换，将顶点坐标从 NDC 坐标系下转换到屏幕坐标系下的坐标，最终将顶点显示在屏幕指定位置上。

以上便是顶点的坐标转换过程。

按照这种规则，我们传给 GPU 的顶点坐标需要遵循裁剪坐标系或者 NDC 坐标系的特点，将顶点坐标控制在 【-1，1】之间，这样的坐标往往掺杂着很多小数，不是很直观。

我们给出的模型坐标一般都是易于理解的，比如：

  • 玩家的坐标是 (10, 10, 20)
  • 箱子长度、宽度、高度都是 10。

但是 GPU 希望接收的是：

  • 玩家坐标(0.2333333, 0.222333, 0.3333444)。
  • 正方体边长 0.333333。

难以理解的小数！

为了将易于理解的起始坐标转换成 GPU 希望 接收的晦涩坐标，于是就有了坐标系的划分，开发者可以专心在各个坐标系内处理对应数据，至于具体的坐标转换过程交给通用的特定转换算法完成。

坐标系分类​

为了将模型坐标转换成裁剪坐标，我们增加了坐标转换流水线。顶点坐标起始于模型坐标系，在这里它被称为模型坐标。模型坐标在 CPU 中经过一系列坐标系变换，生成裁剪坐标，之后 CPU 将裁剪坐标传递给 GPU。

WebGL 坐标系分为如下几类： 模型坐标系 -- 世界坐标系 -- 观察坐标系（又称相机坐标系、视图坐标系） -- 裁剪坐标系（gl_Position接收的值） -- NDC 坐标系 -- 屏幕坐标系。

其中，裁剪坐标系之前的这几个坐标系，我们都可以使用 JavaScript 控制。从裁剪坐标系到 NDC 坐标系，这一个步骤是 顶点着色器的最后自动完成的，我们无法干预。

坐标转换流水线​

  • CPU 中将模型坐标转换成裁剪坐标
    • 顶点在模型坐标系中的坐标经过模型变换，转换到世界坐标系中。
    • 然后通过摄像机观察这个世界，将物体从世界坐标系中转换到观察坐标系。
    • 之后进行投影变换，将物体从观察坐标系中转换到裁剪坐标系。
  • GPU 接收CPU 传递过来的裁剪坐标。
    • 接收裁剪坐标，通过透视除法，将裁剪坐标转换成 NDC 坐标。
    • GPU 将 NDC 坐标通过视口变换，渲染到屏幕上。

img

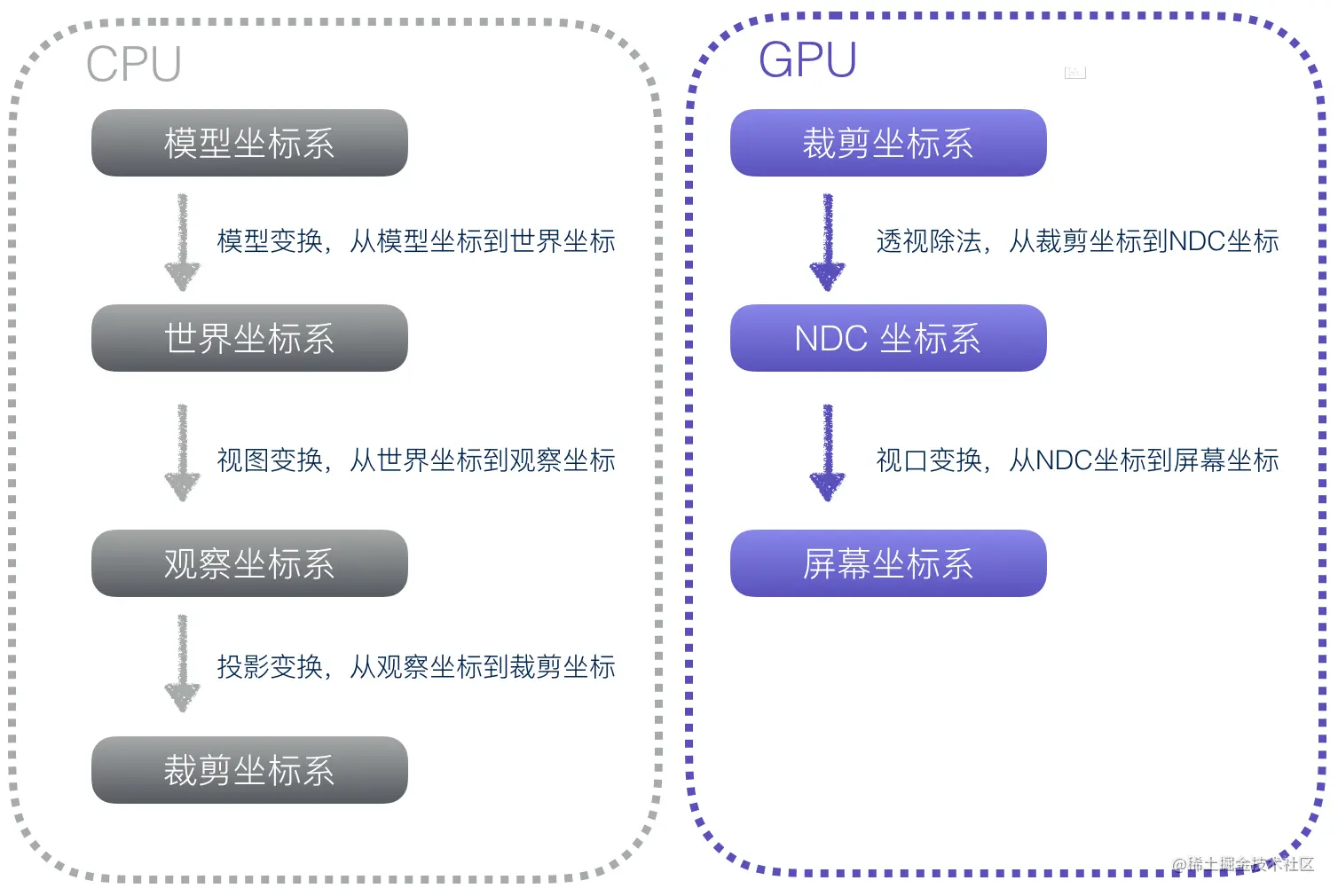
模型坐标系​

一个物体通常由很多点构成，每个点在模型的什么位置？我们需要用一个坐标系来参照，这个坐标系就叫模型坐标系，模型坐标系原点通常在模型的中心，各个坐标轴遵循右手坐标系，即 X 轴向右，Y 轴向上，Z 轴朝向屏幕外。

一般在建模软件中创建模型的时候，各个顶点的坐标都是以模型的某一个点为参照点建立的。

世界坐标系​

我们创建好的模型需要放置在世界中的各个位置，默认情况模型坐标系和世界坐标系重合。如果模型不在世界坐标系中心，那么就需要对模型坐标系进行转换，将模型的各个相对于模型中心的顶点坐标转换成世界坐标系下的坐标。

世界坐标系也是遵循右手坐标系，X 轴水平向右，Y 轴垂直向上，Z 轴指向屏幕外面。

假如模型中有一点 P ，相对于模型中心的坐标（1，1）。 该模型在世界坐标系的（3，0）位置，那么，顶点 P 在世界坐标系中的坐标就变成了（4，1）。

观察坐标系​

观察坐标系是将世界空间坐标转化为用户视野前方的坐标而产生的结果。人眼或者摄像机看到的世界中的物体相对于他自身的位置所参照的坐标系就叫观察坐标系。

在我们日常生活中，精准描述一个街道，我们一般用经纬度来表示，但是如果有人问你：某某街道在什么位置？如果我们告诉他世界坐标：某某街道在东经 M 度，北纬 N 度，我想他会打你。

一般我们都会用这样易于理解的描述：在前面多远，往左或右走多远。

这种坐标就称为观察坐标，也叫相机坐标，他是以人眼/摄像机为原点而建立的坐标系。

之所以有相机坐标系，是为了模仿人眼看待世界的效果。世界很大，有很多物体，但是不能把整个世界都显示到屏幕上，只显示人眼所能看到的一部分，这样我们就能通过改变人眼所处的方位，人眼所在的位置，看到整个 3D 空间的不同部分。

裁剪坐标系​

裁剪坐标是将相机坐标进行投影变换后得到的坐标，也就是 gl_Position 接收的坐标，顾名思义，以裁剪坐标系为参照。

裁剪坐标系遵循左手坐标系。

相机坐标系观察的空间是整个 3D 世界，而裁剪坐标系是希望所有的坐标都落在一个特定的范围内，超出这个范围的顶点坐标都将被裁剪掉，被裁剪掉的坐标就不会显示，这就是裁剪坐标系的由来。

我们将坐标全部表示成【-1.0 , 1.0】之间的方式不是很直观，所以我们希望先将观察空间中的某一部分裁剪出来，这一部分作为要显示的区域。

比如，我们希望将各个坐标轴在 【-1000-1000】 范围内的空间区域作为可视空间区域，这一区域的所有物体都将显示到屏幕上。那么如果一个顶点 P 的坐标是（1300，500，10），那么它就会被裁剪掉，因为它没有坐落在可视空间区域。

img

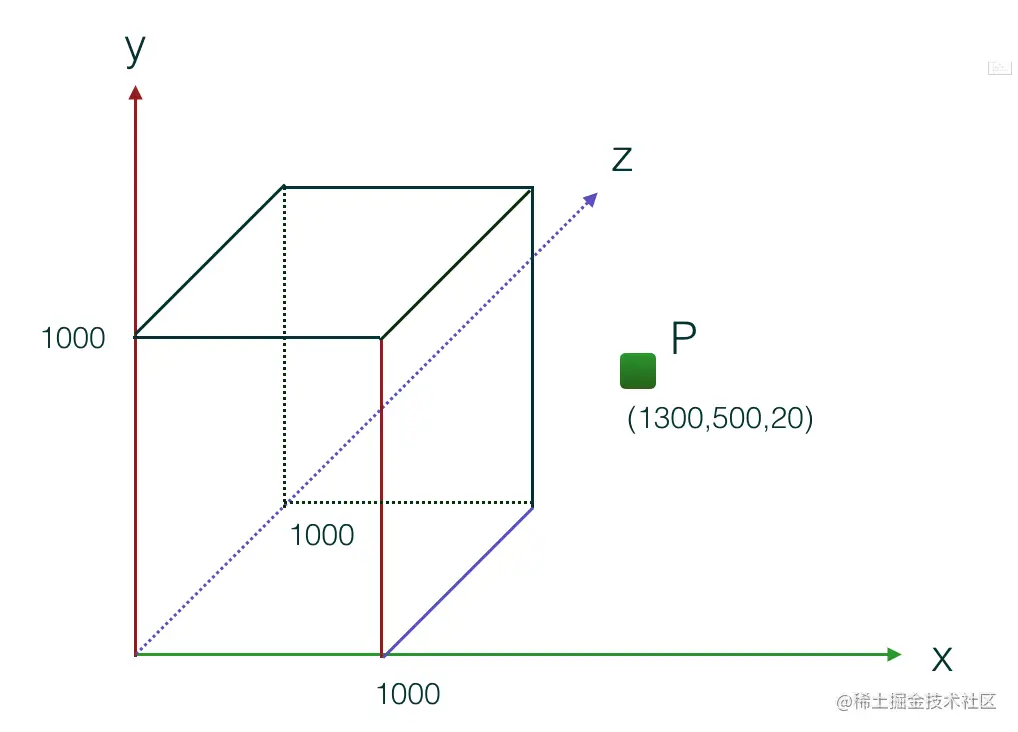
投影矩阵会创建一个观察箱Viewing Box，称为平截头体Frustum，出现在平截头体范围内的坐标最终都会显示在屏幕上。裁剪坐标系中的坐标转化到标准化设备坐标系的过程就很容易，这个过程被称之为投影Projection，使用投影矩阵能将 3D 坐标投影很容易地映射到 2D 的标准设备坐标系中。

将观察坐标变换为裁剪坐标的投影矩阵可以为两种不同的形式，每种形式都定义了不同的平截头体。

正射投影矩阵​

又名正交投影，正射投影矩阵创建的是一个立方体的观察箱，它定义了一个裁剪空间，在该裁剪空间之外的坐标都会被丢弃。 正射投影矩阵需要指定观察箱的长度、宽度和高度。

img

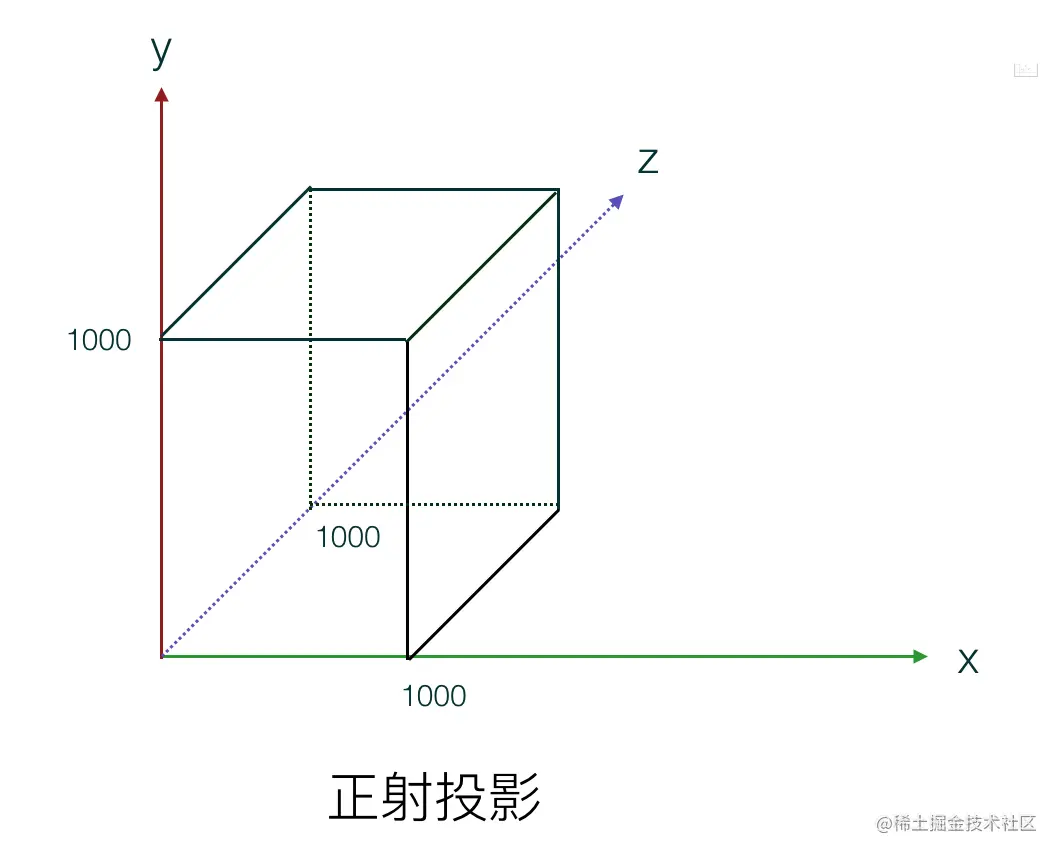
经过正射投影矩阵映射后的坐标 w 分量不会改变，始终是 1，所以在经过透视除法后物体的轮廓比例不会发生改变，这种投影一般用在建筑施工图纸中，不符合人眼观察世界所产生的近大远小的规律。 所以就有了另一种投影：透视投影。

透视投影矩阵​

实际生活中给人带来的感觉是，离我们越远的东西看起来更小。这个奇怪的效果称之为透视Perspective，透视的效果在我们看远处时尤其明显，比如下图：

img

实际上，远处的群山是比近处的房屋大的，但是人眼看上去，群山比房屋小，这就是透视投影要实现的效果。

透视投影矩阵将给定的平截头体范围映射到裁剪空间，除此之外它还会修改每个顶点坐标的 w 值，使得离人眼越远的物体的坐标 w 值越大。被变换到裁剪空间的坐标都会在 -w 到 w 的范围之间（任何大于这个范围的坐标都会被裁剪掉）。WebGL 要求所有可见的坐标都落在【-1.0 - 1.0】范围内，因此，一旦坐标转换到裁剪空间，透视除法就会被应用到裁剪坐标上。

img

透视除法要求顶点坐标的每个分量除以它的 W 分量，距离观察者越远，顶点坐标也就会越小，这就是 W 分量非常重要的另一个原因，它能够帮助我们进行透视投影，经过透视除法后，所有在【-W，W】范围内的坐标都会被转变到 NDC 坐标系中。

透视投影需要设置近平面、远平面、透视深度。

NDC 坐标系​

一旦所有顶点被变换到裁剪空间，GPU 会对裁剪坐标执行透视除法，在这个过程中 GPU 会将顶点坐标的 X，Y，Z 分量分别除以齐次 W 分量。这一步会在每一个顶点着色器运行的最后被自动执行。最终所有坐标分量的范围都会在【-1，1】之间，超出这个范围的坐标都将被 GPU 丢弃。

NDC 坐标系遵循左手坐标系，Z 轴朝向屏幕里面，Z轴值越小，越靠近我们的眼睛，我们可以通过开启 WebGL 的深度检测机制验证一下：

绘制两个三角形，第一个三角形各个顶点 Z 轴坐标为 -0.5，颜色为红色， 第二个三角形各个顶点 Z 轴坐标为 0，颜色为绿色。

开启深度检测前：

img

可以看到，第二个三角形绘制在了前面。不是说左手坐标系吗？按理说 Z 轴越小的越靠近视野，就会显示在前面。其实，在深度检测不开启的情况下，哪个顶点越靠后绘制，哪个顶点就绘制在前面，这时 Z 轴坐标不再决定顶点是否绘制在前面。

开启深度检测后：

img

深度检测开启之后，可以看到 Z 轴小的红色三角形显示在了前面，从而验证了 NDC 坐标系是左手坐标系。

屏幕坐标系​

有了 NDC 坐标之后，GPU 会执行最后一步变换操作，视口变换，这个过程会将所有在【-1, 1】之间的坐标映射到屏幕空间中，并被变换成片段。

我们的模型历尽九九八十一难，终于显示到了屏幕上。

坐标变换举例​

上面的描述大家可能不太理解，接下来我们就以一个简单的例子演示坐标系变换的步骤。

模型坐标​

我们以一个顶点 P 为例，该顶点在边长为 3 的正方体上，初始时顶点所在坐标系是模型坐标系，也就是相对于正方体中心位置，该顶点在模型坐标系中的坐标：

P_m=（3，3，0）

img

世界坐标系​

默认情况下，模型坐标和世界坐标系重合，那该顶点在世界坐标系下的坐标：

P_w = (3, 3, 0)

假设我们将立方体向右移动 5 个单位，向上移动 5 个单位，那么立方体的原点 O 在世界坐标系中的坐标就变成了：

O_w = (5, 5, 0)

那顶点 P 在世界坐标系的坐标也就变成了：

P_w = P_m + O_w = (5+3, 5+3, 0+0) = (8, 8, 0)

img

到这里也很容易理解。

观察坐标系​

世界坐标系中有个人 E 在位置(3, 3, 0)处：

E_w = (3, 3, 0)

E 所看到的世界处于观察坐标系中，X 轴、Y 轴和世界坐标系一致，Z 轴和世界坐标系相反，指向屏幕里面。我们很容易就能想到世界坐标系在观察坐标系中的坐标为：

O_e = -E_w = (-3, -3, 0)

O_e代表世界坐标系的原点在观察坐标系中的坐标。

因此顶点 P 在观察坐标系的坐标就变成了：

P_e = P_w + O_e = (8, 8, 0) + (-3, -3, 0) = (5, 5, 0)

裁剪坐标系​

这里我们为裁剪坐标系指定一个正射投影观察箱，观察箱左侧坐标 -5，右侧坐标 5，上方坐标 5，下方坐标 -5，近平面坐标 0， 远平面坐标 5，那么处于这个观察箱之间的顶点都将被转换到裁剪坐标系中。

由于顶点 P 在观察坐标系的坐标为 (5, 5, 0)，所以它转变到裁剪坐标系下的坐标为：

P_c = (5 / 5, 5 / 5, 0 / 2.5) = (1, 1, 0)

正射投影下， W 分量为 1，到了这一步就有了 W 分量： P_c = (1, 1, 0, 1)

NDC 坐标系​

NDC 坐标是在 GPU 中 将裁剪坐标执行透视除法，所以：

P_n = (1/1, 1/1, 0/1, 1/1) = (1, 1, 0, 1)

坐标没有改变。

视口变换​

接下来该执行视口变换了，视口变换将 NDC 坐标映射到屏幕坐标系。这一步是将 3D 坐标转变成 2D 坐标，在 GPU 中执行，我们无法通过编程干预，

视口我们是通过 WebGL API 中的 gl.viewport来 设置，我们可以设置任意尺寸的视口，这里我们设置宽 500 ，高 300 的尺寸。

gl.viewport(0, 0,  500, 300);

接下来 GPU 就会将 NDC 坐标映射到视口范围内，即将 【-1，1】 的立方体范围内的坐标映射到宽 500，高 300 的屏幕坐标范围。

我们仍然需要先找到 NDC 坐标系原点在 屏幕坐标系中的坐标。

img

由于 NDC 坐标系 X 轴上的一个单位长度就等于视口宽度的一半，Y 轴上的一个单位长度等于视口高度的一半，所以 NDC 坐标系原点在屏幕坐标系下的坐标为

O_s = (250, 150)

又由于 NDC 坐标系 Y 轴方向和 屏幕坐标系 Y 轴方向相反，所以 NDC 坐标系下的 Y 轴坐标转化到屏幕坐标系时要取Y轴坐标的相反数。

那么，顶点 P 转换到屏幕坐标系下的坐标为：

P_s = P_n + O_s = (1 \times 250, -1 \times 150) + (250, 150) = (500, 0)

很明显，顶点显示在 canvas 视口的右上角，这和顶点在裁剪坐标系中设置的观察箱中的位置相吻合。

一个顶点的转换过程大致经历这么几步，我这里只是简单使用坐标偏移演示了一下，其实如果涉及到坐标系的旋转、缩放、Z 轴的加入、透视投影，计算过程将会更复杂。

所幸的是，业界已经有成熟的坐标系变换算法，我们只需要调用他们的方法，传入指定参数，就能生成坐标变换矩阵。

顶点从一个坐标系转换到另一个坐标系，只需要计算出这几点就可以：

  • 计算出原坐标系的原点 O 在新坐标系的坐标。（平移变换）
  • 计算出新坐标系坐标分量的单位向量在原坐标系下的长度。（缩放变换）
  • 计算出原坐标系的坐标分量（基向量）的方向。（旋转变换）

看到平移、缩放、旋转，我们立刻想到了一种快速执行复杂计算的工具：矩阵。

三维坐标系变换​

WebGL原来如此：搞懂三维坐标系变换

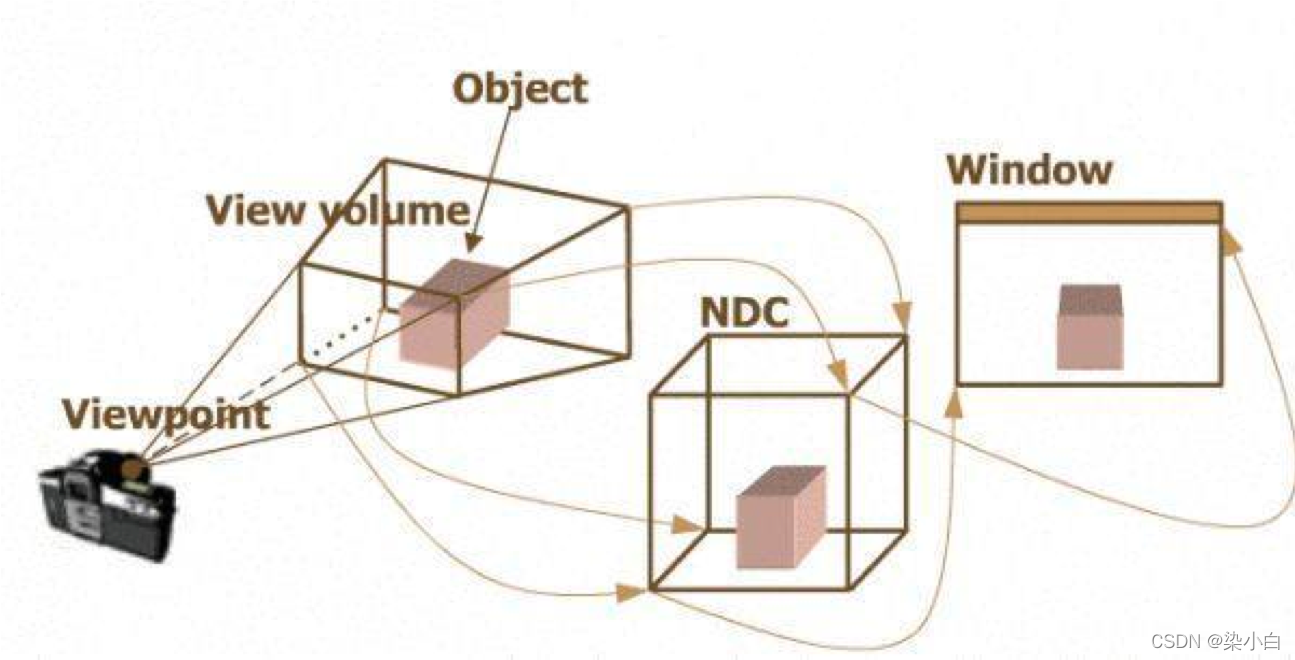img 三维渲染，顾名思义，就是要将多角度可观测的三维物体绘制到一个固定的二维矩形屏幕上，那么三维到二维是如何映射的呢？想必这之间必然经历了一些坐标转换。这也就是前面我说的对图形渲染最基础的认知———坐标转换。

WebGL/OpenGL坐标变换流程图：

img

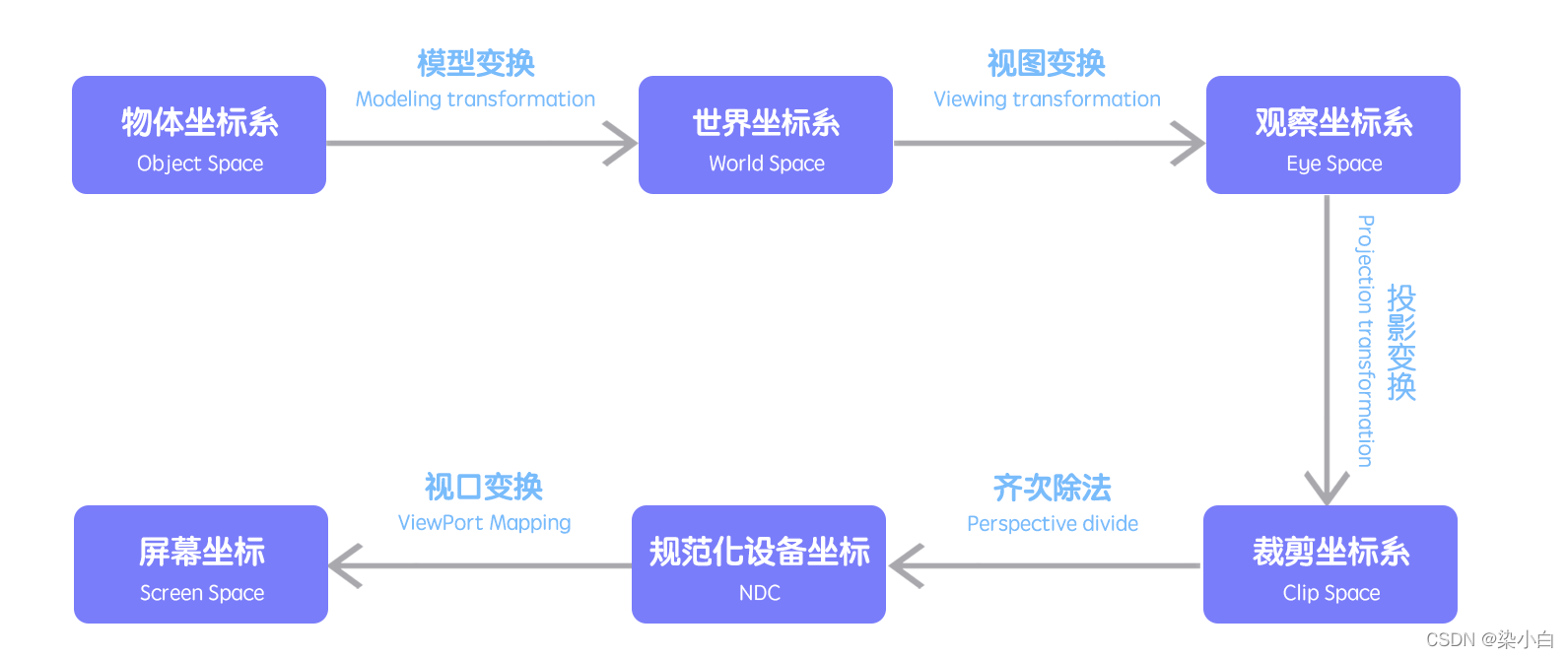
不妨想象一个生活中常见的场景——拍照。

你发现了一处适合拍照的场景，并站过去摆好姿势。（模型变换，model transform）

摄影师找到一个好角度，举起相机对准你。（视图变换，view transform）

摄影师调整焦距，摒除掉干扰物进行拍摄。（投影变换，projection transform）

这就是所谓的MVP变换，整个坐标系变换的核心。

大致有个概念之后，我们再来逐个了解这些变换到底是怎么一回事呢。

一、物体坐标系 -> 世界坐标系（模型变换）​

假设我们想要在屏幕上渲染一只喵和一只汪，对于小喵和小汪这两个模型，他们都有以自己为原点的坐标系，这就是物体坐标系。

世界坐标系可以理解为是这个所有模型共享的虚拟场景空间，要将喵和汪这两个模型都导入到这个大场景中来，并指定其各自的位置。这就需要对物体进行平移、旋转等操作，从而将其摆放到合适的位置上。

这里对物体的操作就是模型变换（Model Transform），将物体坐标与模型矩阵相乘就得到了其在世界坐标系下的坐标。

img

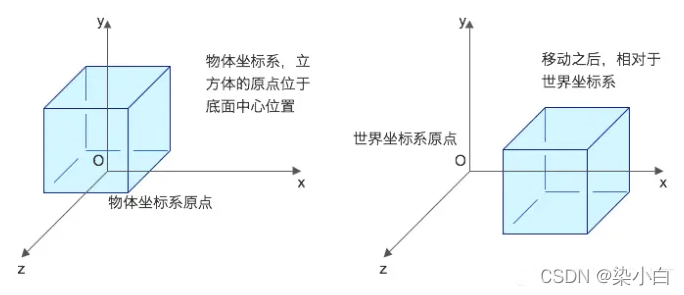
备注：

具体编程中，我们会发现着色器中接收到的顶点坐标在原来(x,y,z)基础上增加了一维1，即齐次坐标，代码如下：

attribute vec3 a_position;
void main() {
    gl_Position = vec4(a_position, 1);
}

之所以使用齐次坐标是由于平移不同于缩放和旋转的线性变换，为了将平移统一进行矩阵计算，就增加一维来做平移，统称为仿射变换。

二、世界坐标系->观察空间（视图变换）​

如同拍摄，对于多角度可观测的三维场景，在屏幕上，我们并不能一下子看到所有视角画面，而是经过摄像机模拟人眼裁剪后所呈现的特定场景。这就需要将坐标变换到以摄像机为原点的观察空间中，该变换过程称为视图变换（View/Camera Transformation）。

我们很容易理解的一个现象，如果物体和相机的相对位置不变的情况下，同时移动相机和物体拍摄出来的结果是一样的。

所以为了计算方便，我们先定义相机的三要素：放置位置在原点（0，0，0）、朝向-z、向上方向为y。

img

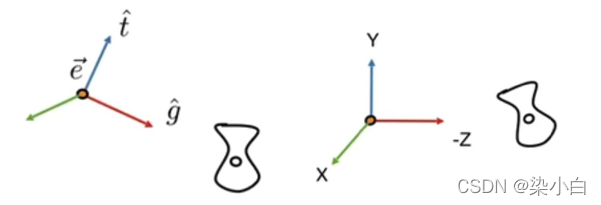
如上图所示，经过平移和旋转将相机变换到约定的位置上来，物体只要相对跟着变换。将平移矩阵与旋转矩阵相乘，就得到了视图变换矩阵Mview = RviewTviewMview=RviewTview。

备注：

1.观察空间使用的是右手坐标系，z轴是摄像机的正前方，故z轴数值表示物体距离摄像机的远近，即深度，此时的深度值还是线性的。

2.如何得到这里的旋转矩阵RviewRviewRview？如果是将任意位置的-g旋转到-z不容易，但反过来容易。所以这里求逆矩阵，并利用“正交矩阵的逆等于转置”性质就得到RviewRviewRview。

3.这样约定相机位置后，结合前一步，其实变换都是作用在了物体上，可以将两个矩阵合并成一个矩阵，也就是大家常说的模型视图变换（ModelView Transform）。

三、观察空间->裁剪空间（投影变换）​

在观察空间中，我们知道只有位于视椎体内的物体才会被摄像机渲染可见，那么对于可见的3D物体如何将其映射到2D平面上呢？就需要接下来的投影变换（Projection Transform）。

投影变换包括了 正交投影（Orthographic Projection） 和 透视投影（Perspective Projection），两者区别由下图显见，正交投影构造的是一个立方体，透视投影构造的是一个上下左右面不平行、远近面大小不一的 视椎体（frustum），所以正交投影变换得到的远近物体大小都一样，而透视投影变换能产生近大远小的效果。

img

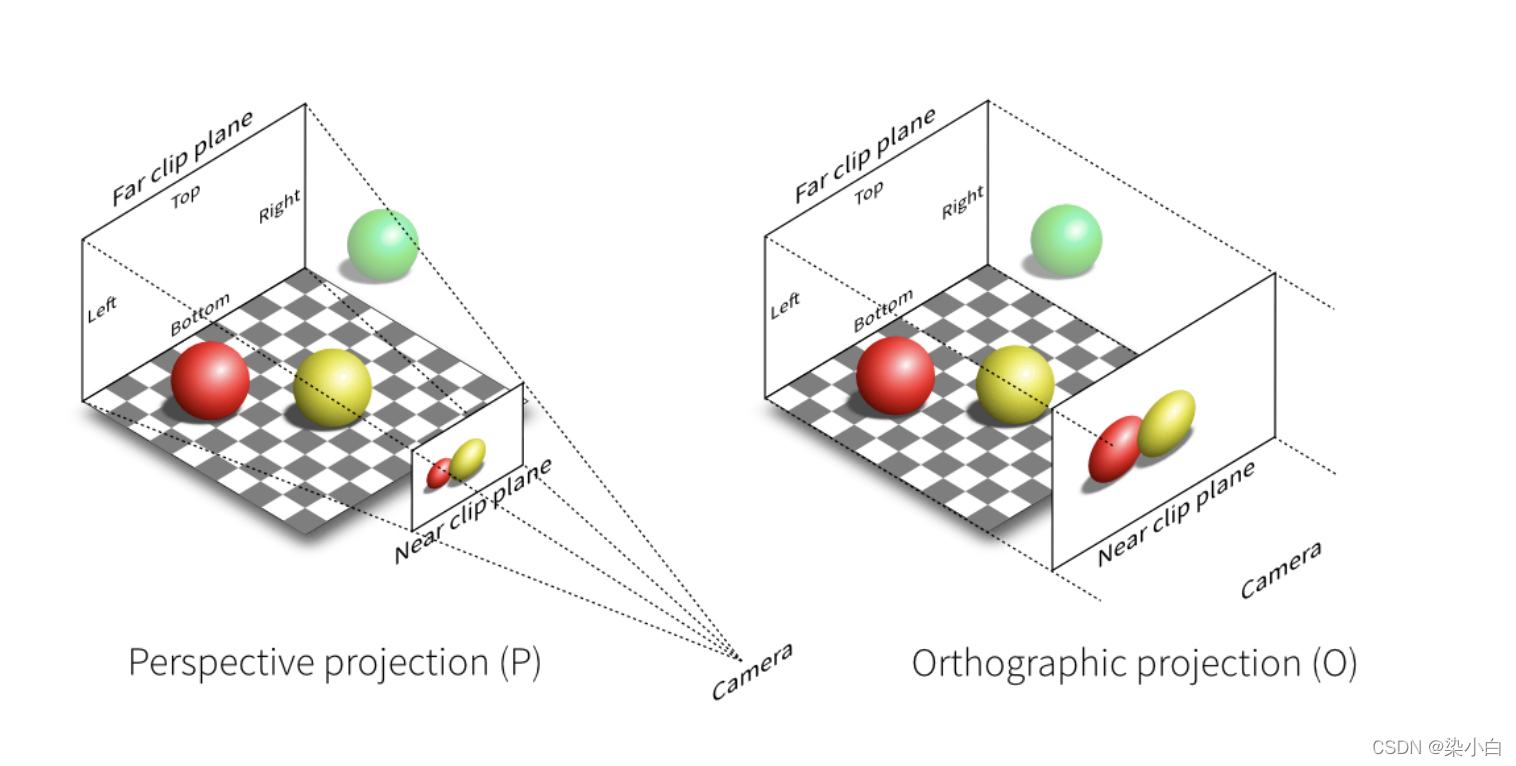
要实现远近裁剪面内的物体能够投影到近平面上，正交投影的标准立方体就很容易实现，但对于透视投影远平面大于近平面的情况就比较复杂。那么拆解问题，首先挤压椎体上下左右平面将其变成跟正交投影一样的立方体，然后再进行正交投影即可。

挤压规则约定三点：① 近平面不变；② 远平面z值不变；③ 远平面中心点不变；

再结合相似三角形性质，可以推导出将透视投影变换到正交投影的矩阵。

此外，对于视椎体定义两个变量：

① 宽高比aspect ratio = width / height；

② 垂直可视角fovY

img

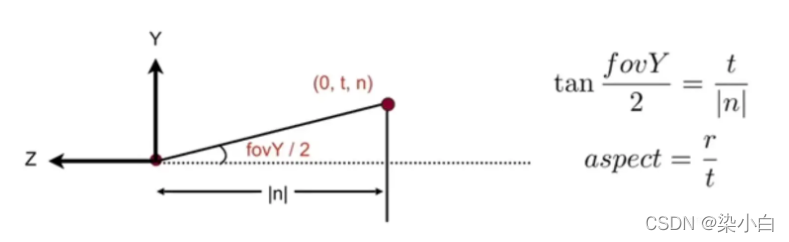
最终得到的透视矩阵：

  • near：近裁剪平面距离

  • far：远裁剪平面距离

  • fov：椎体竖直方向的张开角度（当视野更大时，物体通常变小）

  • aspect：摄像机的宽高比（该参数解决了当画布调整大小和形状时模型的变形问题）

    至此，经过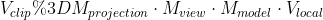V_{clip} = M_{projection}\cdot M_{view} \cdot M_{model} \cdot V_{local}变换得到了裁剪坐标。转换过程中对x,y,z分量都进行了不同程度的缩放和平移，x,y是屏幕横纵坐标，z是垂直屏幕的深度坐标。裁剪是将变换后的x,y,z与w值作比较，如果位于[-w,w]范围内保留，否则剔除。

备注：

1、由于矩阵乘法很耗时，并且矩阵具有结合律，通常我们会将MV矩阵先相乘得到一个模型视图矩阵。

2、性质：将齐次坐标(x,y,z,1)每个分量都乘以不等于0的常数k，得到的（kx,ky,kz,k）在3D空间中与（x,y,z,1）表示同一个点。

3、透视矩阵需要注意的是，会翻转z轴。裁剪空间坐标系是左手坐标系（z轴指向远离观察者并指入屏幕的位置）。

四、裁剪空间 -> 标准化设备空间（齐次除法）​

经过前面的变换，我们在视椎体中得到裁剪后要展示的部分，接下来要将视椎体内物体映射到近平面上，以在2D平面上展示。

就需要将坐标转换到一个与硬件设备无关的 规范化设备坐标（NDC, Normalized Deviced Coordinates），以描述映射到近平面上的坐标，这一步的变换称为 齐次除法 或 透视除法，即将x,y,z分量分别除以w分量，将其变换到[−1,1]3[-1,1]^3[−1,1]3范围内。以x轴为例转换公式： （公式）

在这之前，为了方便仿射变换，我们一直使用的是齐次坐标（x,y,z,w），经过齐次除法变换回笛卡尔坐标（x,y,z）。如下图所示，变换后的原点在（0,0,0），xyz分量均为2个单位的立方体中，并且z轴进行了翻转（由右手系变成左手系）。

img

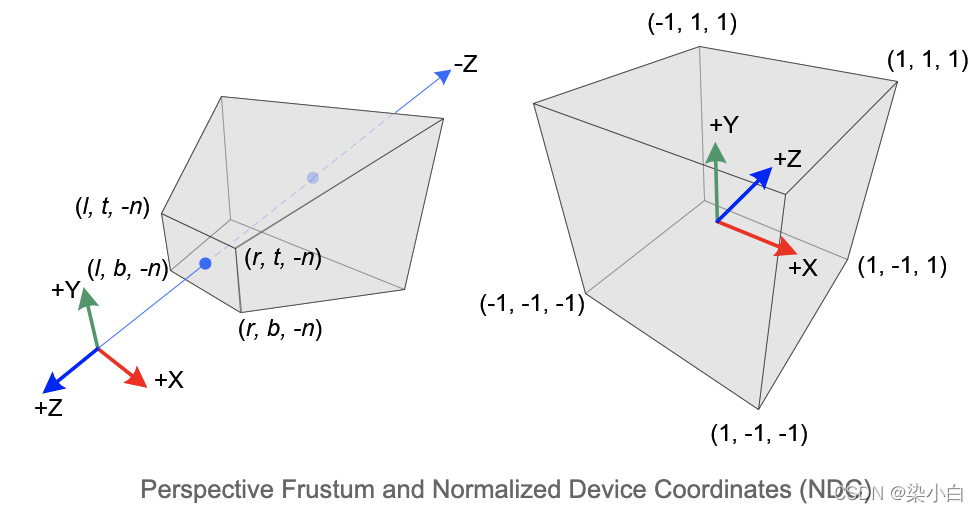
备注：

做完投影变换与齐次除法后，物体坐标都变换到[-1, 1]^3[−1,1]3范围内，会导致物体拉伸，后面还会进行一次视口变换再拉伸回来。

五、标准设备空间 -> 屏幕坐标（视口变换）​

最后一步视口变换，将NDC的[−1,1]3[-1,1]^3[−1,1]3立方体中的坐标变换为视口坐标（屏幕坐标），从而在屏幕上进行像素绘制。

WebGL绘制的画布是canvas元素，定义左下角为坐标原点，右上角像素坐标为（pixelWidth, pixelHeight）。

img

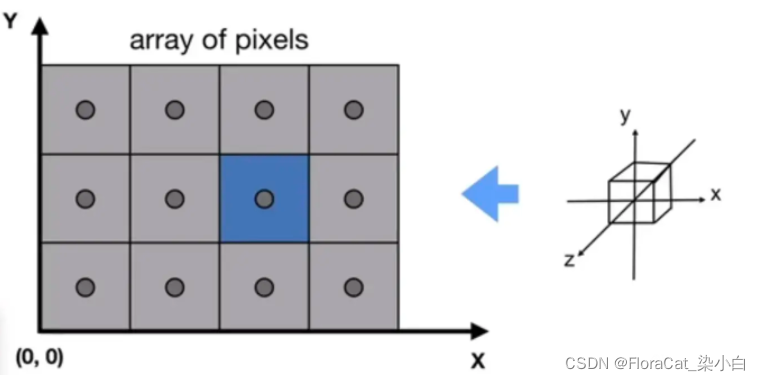
这个坐标变换只对x,y进行操作，由 [-1,1]^2[−1,1]2 变换到 [0,width]*[0,height] 范围。如下面矩阵所示，对x和y进行缩放拉伸，并将其移到屏幕的原点。实现了标准设备坐标与屏幕窗口像素的一一对应。

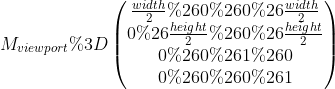
M_{viewport}=\begin{pmatrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \ 0 & \frac{height}{2} & 0 & \frac{height}{2}\ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1 \end{pmatrix}

在webgl中有直接设置视口(ViewPort)的方法：

gl.viewport(0, 0, this.cvs.width, this.cvs.height); 等等，那z坐标呢？经过前面齐次除法得到的z分量用来表示深度信息，将被用于深度缓冲（Z-buffer）算法，计算每个像素的深度测试，以实现正确的遮挡效果。这属于着色内容